Indice
- 9 Ottimizzazione bivariata
- 9.1 Funzioni reali di due variabili
- 9.2 Derivate parziali del primo ordine
- 9.3 Derivate del secondo ordine e matrice Hessiana
- 9.4 Massimo e minimo di una funzione di due variabili
- 9.5 Ottimizzazione su un insieme aperto
- 9.6 Ottimizzazione vincolata con vincoli sostituibili
- 9.7 Il metodo dei moltiplicatori di Lagrange
- 9.8 Massimo e minimo su dominio chiuso e limitato
- 9.9 Esercizi riassuntivi
- 9.10 Il modello di regressione lineare
- 9.11 Esercizi
In questo capitolo studieremo come trovare i punti di massimo e di minimo di una funzione di due variabili. Per farlo, generalizzeremo tutti i concetti che ci hanno permesso di studiare le funzioni di una variabile, rendendoli idonei ad essere trattati su un dominio a due dimensioni.
9.1 Funzioni reali di due variabili
L’oggetto di studio di questo capitolo sono le funzioni del tipo
Anche una funzione reale di due variabili
Per un insieme a due dimensioni, è necessario dare una nuova definizione di intorno di un punto.
Definizione 9.1Si dice intorno del punto
Data la definizione di intorno, tutte le definizioni topologiche viste nel Capitolo 1 quali quelle di punto interno, punto di frontiera, punto di accumulazione, insieme aperto ed insieme chiuso, restano invariate. Nella figura seguente possiamo quindi apprezzare la differenza tra un sottoinsieme aperto di
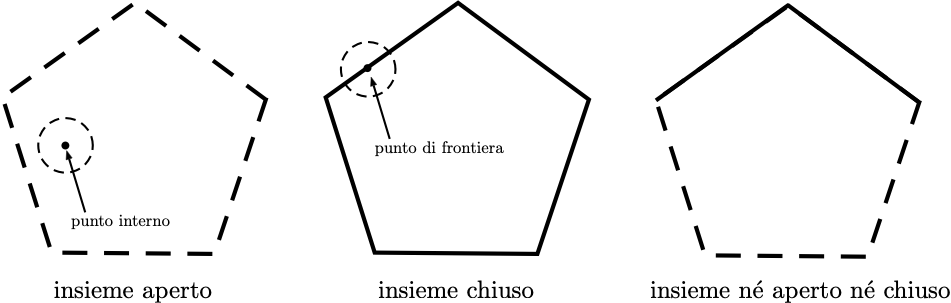
Il nuovo concetto di intorno permette di estendere direttamente le definizioni di limite (ci limitiamo al concetto di limite nell’intorno di un punto) e continuità di una funzione.
Definizione 9.2Siano dati la funzione
Definizione 9.3Una funzione
Analogamente al caso univariato (unidimensionale), segue nel caso bivariato (bidimensio-nale) che:
- tutte le funzioni che tratteremo nel seguito di questo capitolo sono continue sul loro dominio naturale;
- la somma, differenza, quoziente, composizione di funzioni continue, laddove correttamente definite, sono continue sul loro dominio naturale.
Per le funzioni di due variabili, il dominio naturale viene definito in modo completamente analogo alle funzioni di una variabile.
Definizione 9.4Per una funzione
Analogamente al caso unidimensionale, un restringimento del dominio naturale di una funzione può essere causato da:
- la presenza di una frazione, in cui il denominatore deve essere non nullo;
- la presenza di una radice quadrata, il cui argomento deve essere non negativo;
- la presenza di un logaritmo, il cui argomento deve essere positivo.
Per una funzione a due variabili, il dominio naturale (essendo un sottoinsieme di
) può essere raffigurato sul piano cartesiano. La rappresentazione del dominio non deve essere confusa con il grafico della funzione, che è invece tridimensionale e quindi dovrà essere raffigurato in tre dimensioni.
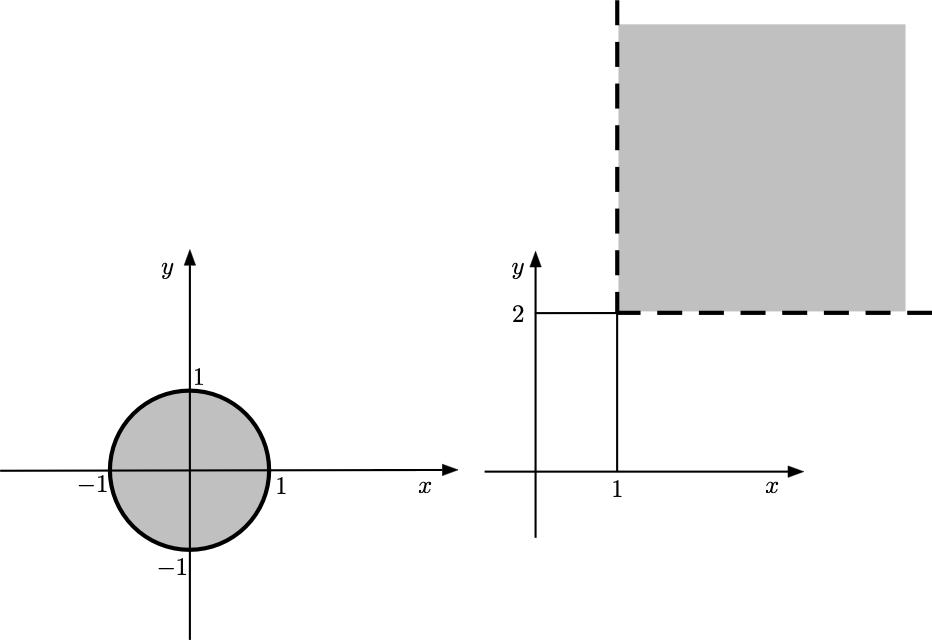
Example 9.1Si trovi il dominio naturale della funzione
Example 9.2Si trovi il dominio naturale della funzione
9.2 Derivate parziali del primo ordine
Analogamente al caso univariato, il calcolo delle derivate si rivelerà strumento essenziale per l’ottimizzazione di una funzione bivariata.
Il concetto di derivata per una funzione di due variabili viene definito nel modo più semplice ed intuitivo possibile: se si fissa una variabile nella funzione
Definizione 9.5Data la
- derivata parziale rispetto alla prima variabile (rispetto a
- derivata parziale rispetto alla seconda variabile (rispetto a
Nel caso esistano le due derivate parziali, esse si dicono derivate del primo ordine.
Quando esiste, la derivata parziale
si calcola fissando il valore della e derivando la funzione rispetto a (assumendo quindi costante); la derivata parziale si calcola analogamente fissando il valore della e derivando la funzione rispetto a (assumendo quindi costante). Si deduce quindi che si è già in grado di calcolare le derivate parziali di una funzione di due variabili perché esse non sono altro che le derivate delle funzioni di una variabile ottenute fissando prima la , e poi la .
Per semplicità di notazione, scriveremo
e nel seguito.
Example 9.3Si calcolino le derivate parziali della funzione
Si osservi prima di tutto che, essendo la funzione un polinomio (una somma del prodotto di potenze in
Assumendo costante la
Example 9.4Si calcolino le derivate parziali della funzione
Assumendo costante la
Example 9.5Si calcolino le derivate parziali della funzione
Prima di tutto è necessario richiedere che l’argomento del logaritmo sia positivo, quindi
9.3 Derivate del secondo ordine e matrice Hessiana
Dato che le derivate parziali di una funzione a due variabili sono a loro volta funzioni di due variabili, è naturalmente possibile definire le derivate parziali delle derivate parziali, che prenderanno il nome di derivate parziali del secondo ordine.
Nel caso i corrispondenti limiti esistano finiti, si hanno dunque quattro derivate:
- la derivata di
- la derivata (mista) di
- la derivata (mista) di
- la derivata di
Nel caso esistano, le quattro derivate del secondo ordine della funzione
Calcolare la matrice Hessiana di una funzione non comporta nessuna difficoltà aggiuntiva rispetto a quanto fatto sino a questo punto, tranne il fatto di dover calcolare quattro nuove derivate di funzioni di una variabile. Calcoliamo quindi la matrice Hessiana negli esempi precedenti.
Example 9.6Riprendendo l’Esempio 9.3, si calcoli la matrice Hessiana della funzione
Ricordando che
Example 9.7 Riprendendo l’Esempio 9.4, si calcoli la matrice Hessiana della funzione
Example 9.8 Riprendendo l’Esempio 9.5, si calcoli la matrice Hessiana della funzione
Negli esempi precedenti le due derivate miste del secondo ordine sono identiche. È infatti possibile dimostrare il seguente teorema, che vale nella totalità dei casi trattati in questo testo.
Theorem 9.1 (Teorema di Schwarz) Se la funzione
Il Teorema di Schwarz non deve fornire una scorciatoia per velocizzare il calcolo della matrice Hessiana evitando il calcolo di una delle due derivate miste, ma piuttosto un efficace strumento per verificare se il calcolo delle due derivate miste è stato effettuato correttamente.
9.4 Massimo e minimo di una funzione di due variabili
Esattamente come nel caso univariato, il massimo/minimo assoluto di una funzione di due variabili è definito come il massimo/minimo dei valori assunti dalla funzione, ovvero il massimo/minimo della sua immagine. Analogamente, se ci si restringe a considerare un intorno di un punto, si parlerà di massimo/minimo locale (anche detto relativo).
Se la funzione in oggetto deve essere ottimizzata, ovvero se ne devono cercare eventuali massimo e minimo, essa prenderà il nome di funzione obiettivo.
Definizione 9.6 Data una funzione
Definizione 9.7 Data una funzione
Segue immediatamente dalla definizione che un punto di massimo/minimo assoluto è anche locale, ma non viceversa.
In generale se si parla di massimo/minimo di una funzione (senza aggiungere un aggettivo), si intende il massimo/minimo assoluto. Nei grafici delle funzioni di seguito, identificheremo i punti di massimo/minimo locale o assoluto con un circoletto pieno.
L’ottimizzazione di una funzione bivariata procede analogamente a quella di una funzione univariata. Una funzione può avere punti di massimo/minimo:
- nei punti interni al suo dominio;
- nei punti di frontiera inclusi nel suo dominio.
Nella sezione di seguito, cominceremo ad analizzare il caso in cui il dominio della funzione sia aperto, ovvero tutti i punti del suo dominio risultino essere interni.
9.5 Ottimizzazione su un insieme aperto
Assumiamo che un punto
Theorem 9.2 (Condizione del primo ordine per punti di massimo/minimo) Data la funzione
La condizione del primo ordine non è sufficiente a garantire che un punto stazionario sia in effetti un punto di massimo/minimo, locale o assoluto, ma è solamente un requisito necessario. Analizziamo due diversi esempi in cui la condizione è soddisfatta.
Example 9.9 Si consideri la funzione
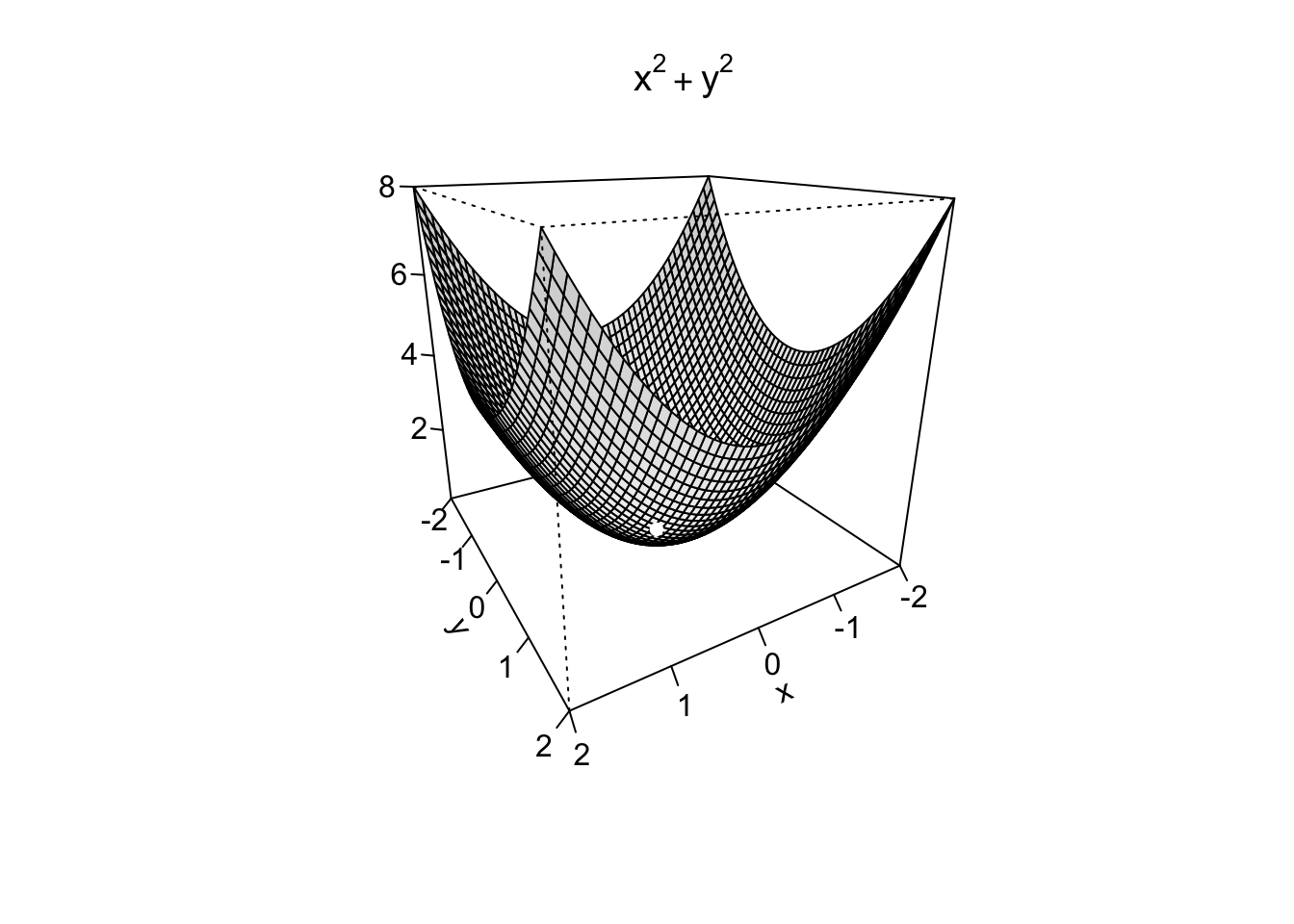
Example 9.10 Si consideri adesso la funzione
Si osservi infatti che la funzione
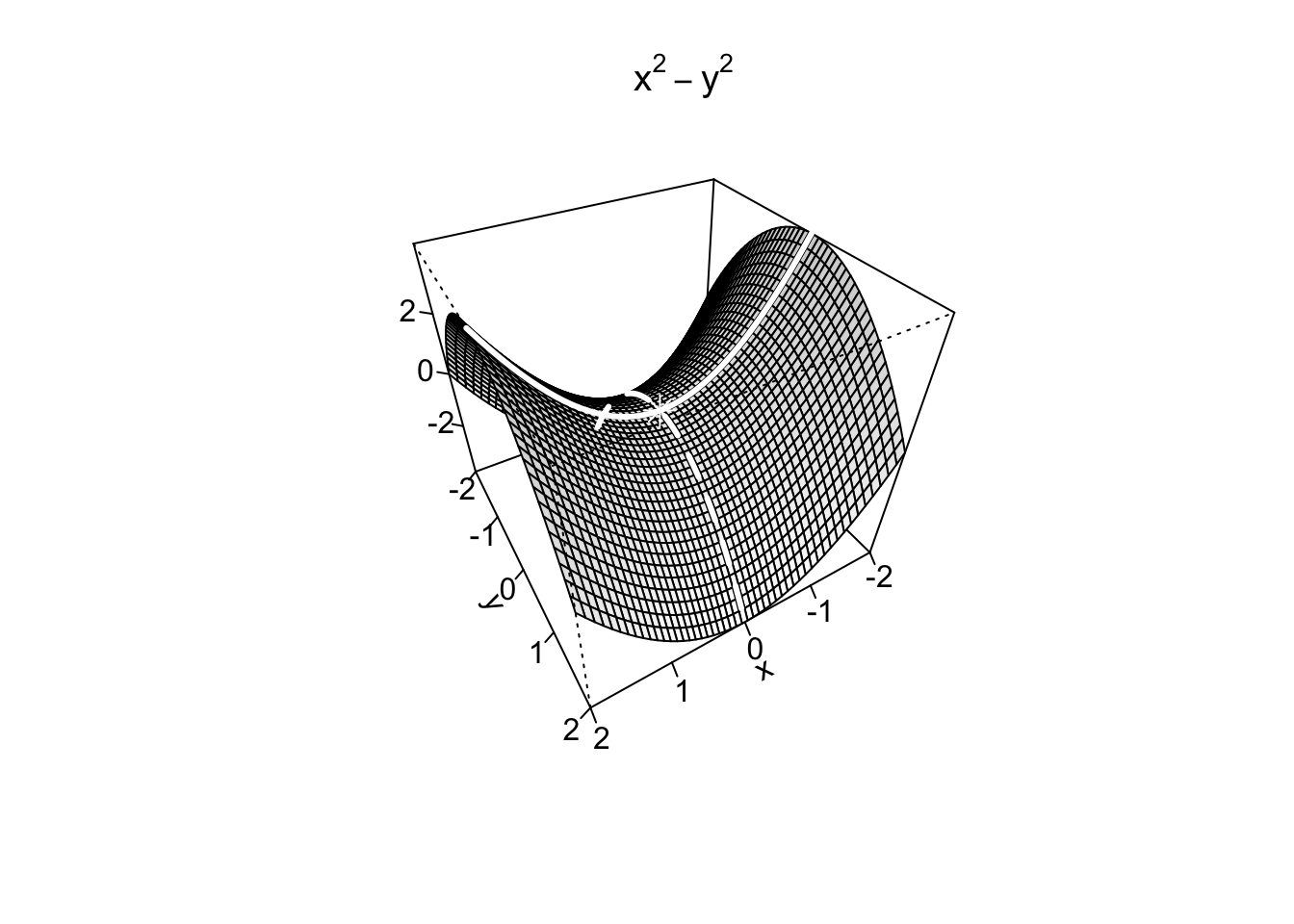
Definizione 9.8 Data una funzione
Nei grafici delle funzioni di seguito, identificheremo i punti di sella con un asterisco.
Per poter stabilire la natura di un punto stazionario, come nel caso univariato, è quindi necessario reperire una informazione migliore di quella fornita dalle derivate del primo ordine. Nel caso bidimensionale, non è nemmeno sufficiente studiare il segno delle derivate parziali, come si vede dall’esempio appena svolto. Condizioni sufficienti per garantire l’esistenza di un massimo/minimo interno si devono necessariamente basare sulle derivate del secondo ordine.
Per enunciare le condizioni del secondo ordine, ricordiamo la definizione di determinante di una matrice
Definizione 9.9 Si dice determinante della matrice Hessiana
Inoltre, è necessario assumere che il dominio
Theorem 9.3 (Condizioni del secondo ordine per punti di massimo/minimo ASSOLUTI) Sia
Se, per ogni
Remark. Osserviamo i seguenti punti fondamentali sul Teorema 9.3:
- le due condizioni corrispondono al caso in cui la funzione sia concava (
- le condizioni del teorema sono sufficienti ad identificare un punto di massimo/minimo assoluto ma sono anche molto forti: devono valere sull’intero dominio (aperto e convesso) della funzione;
- il teorema nulla predice nel caso in cui non valgano le condizioni citate, né le sue condizioni sono necessarie: è possibile trovare funzioni aventi un punto di massimo/minimo assoluto che non le soddisfano;
- entrambe le condizioni sono soddisfatte ad esempio dalla funzione costante (sia concava che convessa) in cui ogni punto è stazionario (le derivate del primo ordine sono nulle) ed è sia di massimo che di minimo (tutte le derivate del secondo ordine sono nulle).
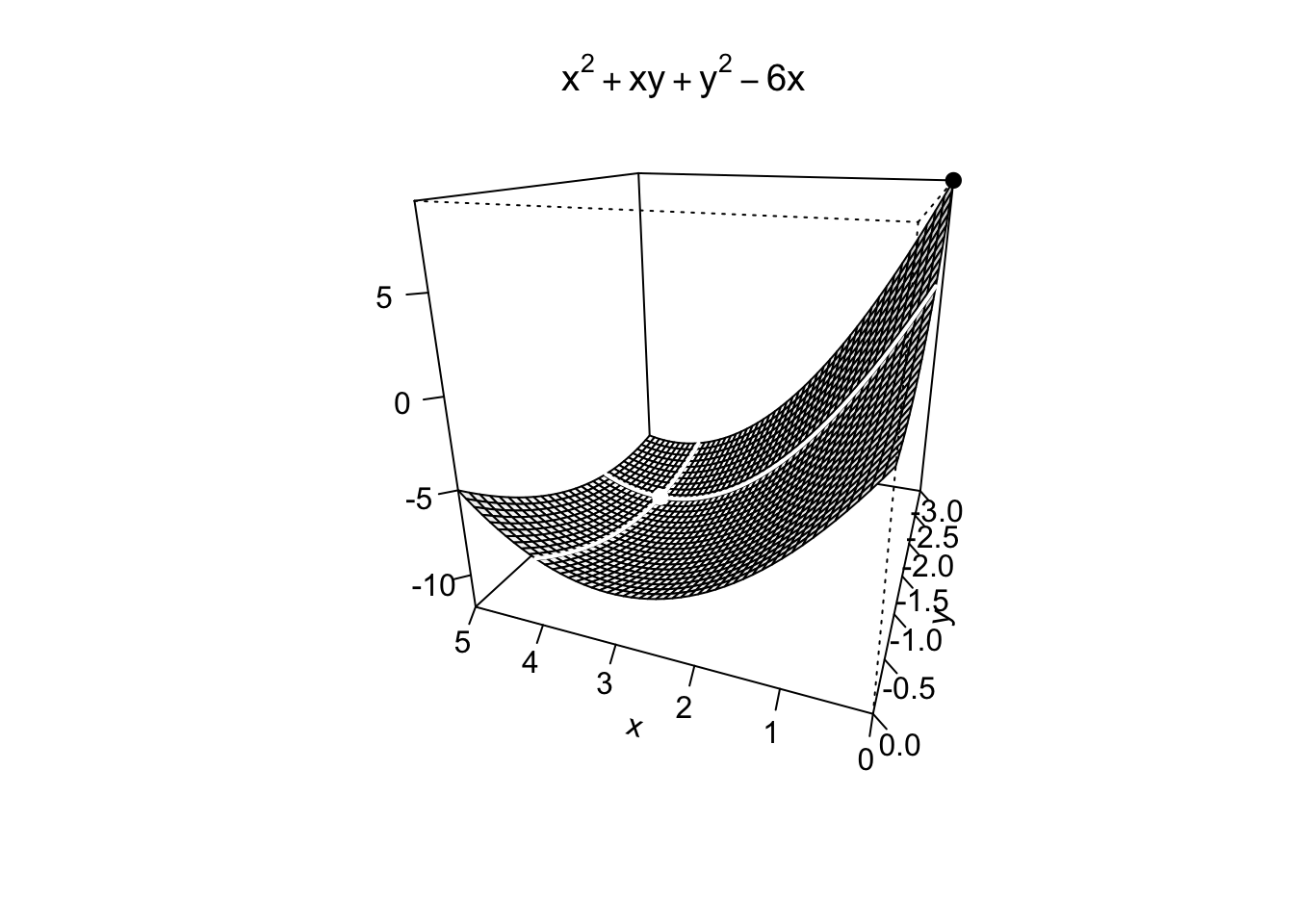
Example 9.11 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione
Si cercano quindi eventuali punti stazionari della funzione calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema:
Controllando quindi le condizioni del Teorema 9.3, per ogni 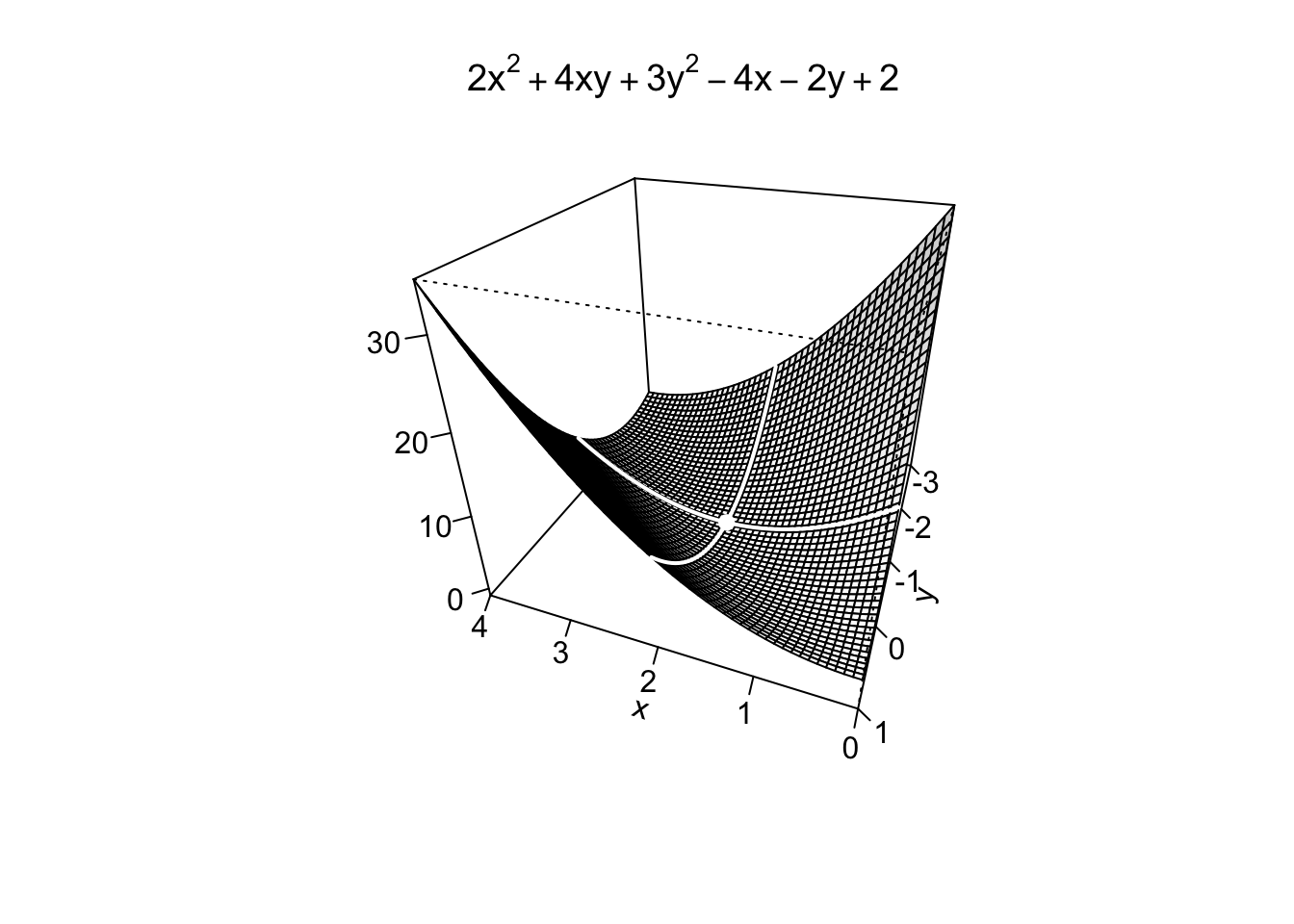
Example 9.12 Si trovino e si classifichino tutti i punti stazionari della funzione
Si cercano i punti stazionari della funzione calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema:
Il sistema rappresentante la condizione di annullamento delle due derivate parziali non è in generale lineare, nè si presta ad un metodo di risoluzione generale. Quando è possibile, si può operare per sostituzione o, come in questo caso, discutere i casi implicati dalla legge di annullamento del prodotto, se una delle due equazioni è una moltiplicazione tra due fattori.
Per trovare tutti i punti stazionari, si discutono i seguenti casi:
- se
- se
- nel caso rimanente, ovvero se
Risultano quindi i quattro punti stazionari:
In casi come quelli descritti nell’esempio precedente, le forti ipotesi del Teorema 9.3 non sono soddisfatte. Serve quindi un risultato che abbia una maggiore applicazione.
Theorem 9.4 (Condizioni del secondo ordine per punti di massimo/minimo LOCALI) Sia
- Se
- se
Remark. Osserviamo i seguenti punti fondamentali sul Teorema 9.4:
- le due condizioni corrispondono al caso in cui la funzione sia strettamente concava (
- le condizioni del Teorema 9.4 sono applicabili in un numero di casi maggiore rispetto al Teorema 9.3, ma le sue conclusioni sono forzatamente più deboli e hanno valore locale (relativo) ma non assoluto (globale). È semplice capirne il motivo: la matrice Hessiana calcolata in un punto non potrà mai fornire informazioni su tutto il dominio della funzione, ma solo relativamente ad un intorno di quel punto. L’informazione data da questo teorema ha quindi carattere locale, e non globale;
- il teorema nulla predice nel caso in cui non valgano le condizioni citate, come ad esempio nel caso in cui
Possiamo utilizzare il Teorema 9.4 per completare l’Esempio 9.12.
Example 9.13Si trovino e si classifichino tutti i punti stazionari della funzione
Nell’Esempio 9.12 si erano trovati i quattro punti stazionari
Come già osservato, le conclusioni del Teorema 9.4 non possono avere carattere globale. Resta dunque da determinare se i punti di massimo/minimo relativo trovati siano anche assoluti.
Per farlo, si può ad esempio verificare se la funzione è illimitata. Dato che compare il termine
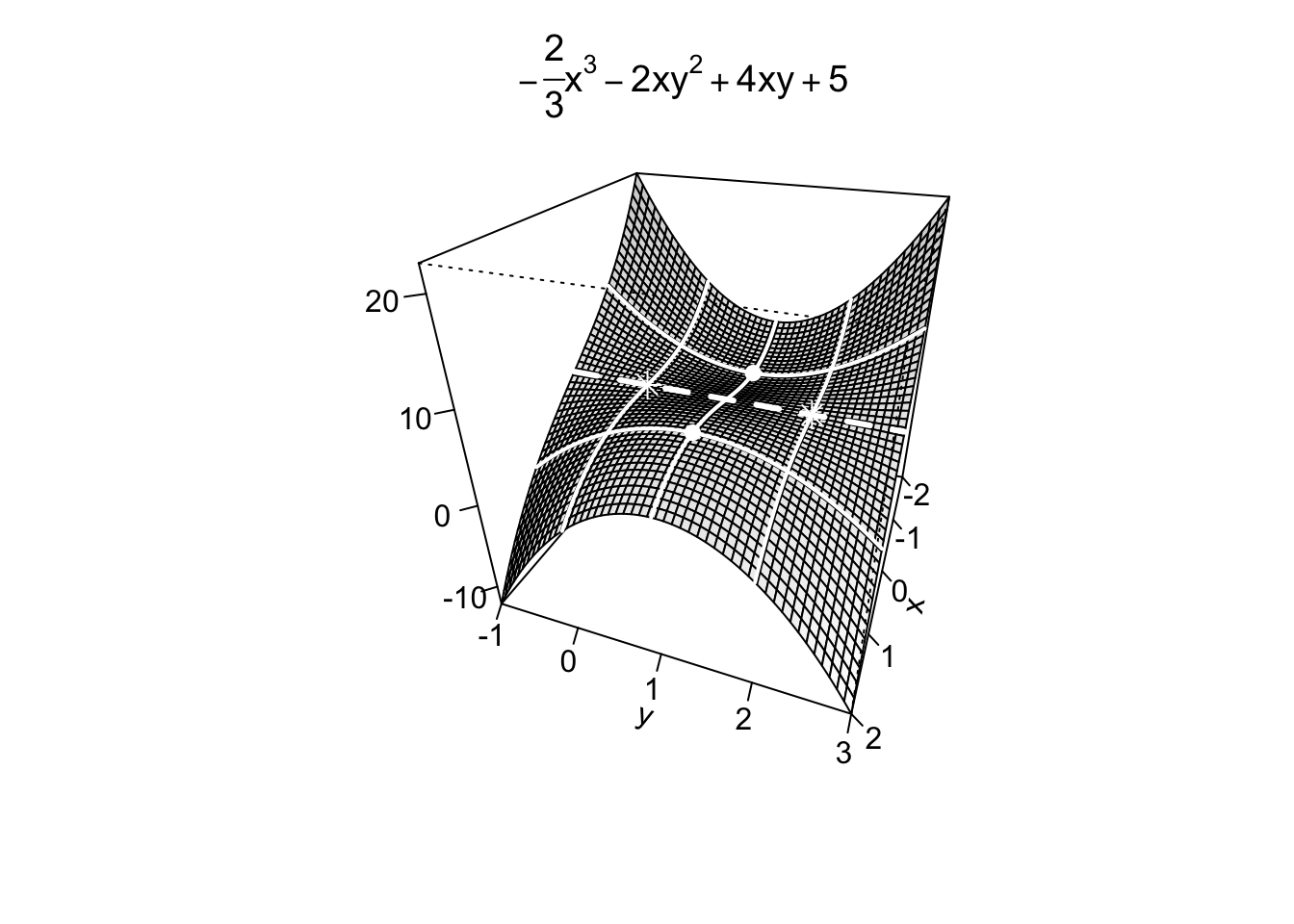
Se, fissando opportunamente una delle due variabili, la funzione risulta essere illimitata superiormente (inferiormente), si ha la certezza dell’inesistenza di un massimo (minimo) assoluto. Viceversa, se questo non risultasse vero o non si scegliesse idoneamente il valore della variabile da fissare, il problema della determinazione della natura del punto stazionario in oggetto rimarrebbe aperto, rendendo necessario un ulteriore approfondimento. In generale, l’ottimizzazione in più dimensioni è un problema difficile, anche numericamente, e non è al momento noto un algoritmo di risoluzione generale.
Attenzione al testo dell’esercizio! Se nell’Esempio 9.13 fosse stato chiesto di ottimizzare la funzione (trovare il suo massimo/minimo assoluto), sarebbe stato sufficiente calcolare gli ultimi due limiti per dimostrare che le funzione non ammette nè massimo nè minimo assoluto.
Schema di risoluzione completo di una ottimizzazione su un insieme aperto (A):
- si controlla che il dominio sia aperto: tutti i suoi punti sono interni (caso A);
- eventuali massimi/minimi relativi/assoluti possono essere raggiunti solo su punti stazionari, che quindi si ricercano uguagliando a zero le due derivate parziali;
- si calcola la matrice Hessiana per determinare la natura dei punti stazionari trovati;
- si stabilisce se si può utilizzare il Teorema 9.3 per ottenere delle conclusioni globali, oppure il Teorema 9.4 per ottenere delle conclusioni locali;
- si cerca di stabilire se eventuali punti di massimo/minimo relativo siano anche assoluti (questo punto si può affrontare immediatamente a seconda della richiesta del problema da risolvere).
Example 9.14Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione
Si cercano quindi eventuali punti stazionari della funzione calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema:
Per capirne la natura, si calcola la matrice Hessiana
Ai fini dell’applicazione del Teorema 9.3 è rilevante che il segno di
permanga positivo su tutto il dominio, non che la matrice Hessiana sia costante (non dipenda dal punto ).
Si osservi che la funzione non può avere un punto di massimo, perché è illimitata superiormente, come si può ad esempio verificare fissando il valore
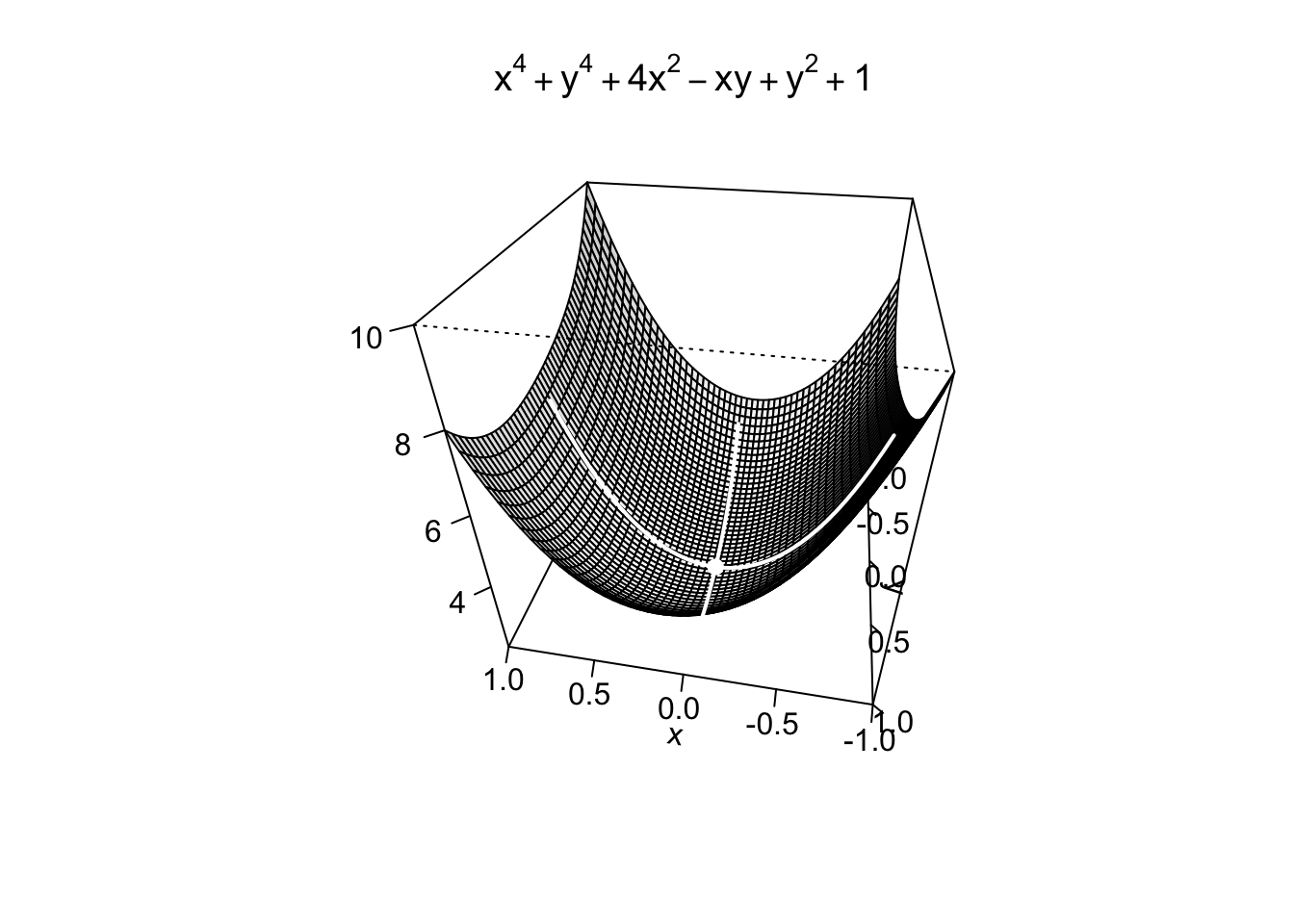
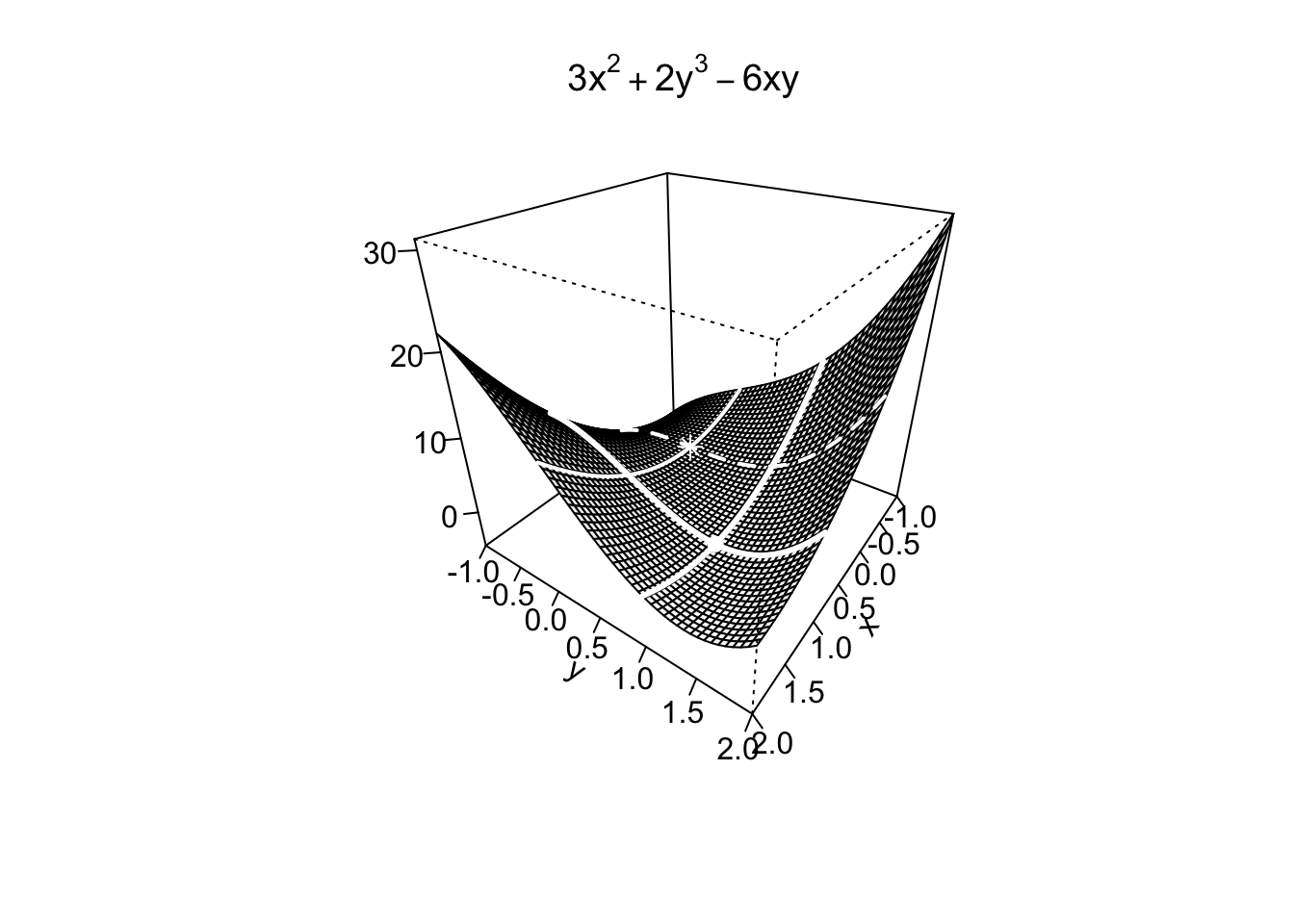
Example 9.15Si trovino e si classifichino tutti i punti stazionari della funzione
Si cercano i punti stazionari della funzione calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema:
Per determinarne la natura, si calcola la matrice Hessiana
La funzione non ammette (punto di) massimo assoluto, altrimenti lo avremmo trovato tra i punti stazionari. Resta dunque da determinare se il punto di minimo relativo trovato sia anche assoluto o meno.
Per farlo, si verifica, fissando
9.6 Ottimizzazione vincolata con vincoli sostituibili
Molto spesso le funzioni sono ottimizzate tenendo conto di condizioni (vincoli) che ne restringono il dominio sul quale cercare i punti di massimo/minimo. Il nuovo dominio, differente quindi dal dominio (naturale) della funzione, è detto dominio di ottimizzazione.
Iniziamo con lo studiare problemi di ottimizzazione vincolata considerando i casi più semplici in cui il dominio è ristretto da uno o più vincoli che si possono direttamente sostituire all’interno della funzione da ottimizzare, trasformando così l’ottimizzazione da bivariata ad univariata.
Example 9.16Tra tutti i rettangoli di semi-perimetro fissato, si determinino quelli aventi area massima e minima.
Questo è un problema classico che illustra come operare con vincoli che si possono sostituire direttamente all’interno della funzione da ottimizzare (caso B).
Detti
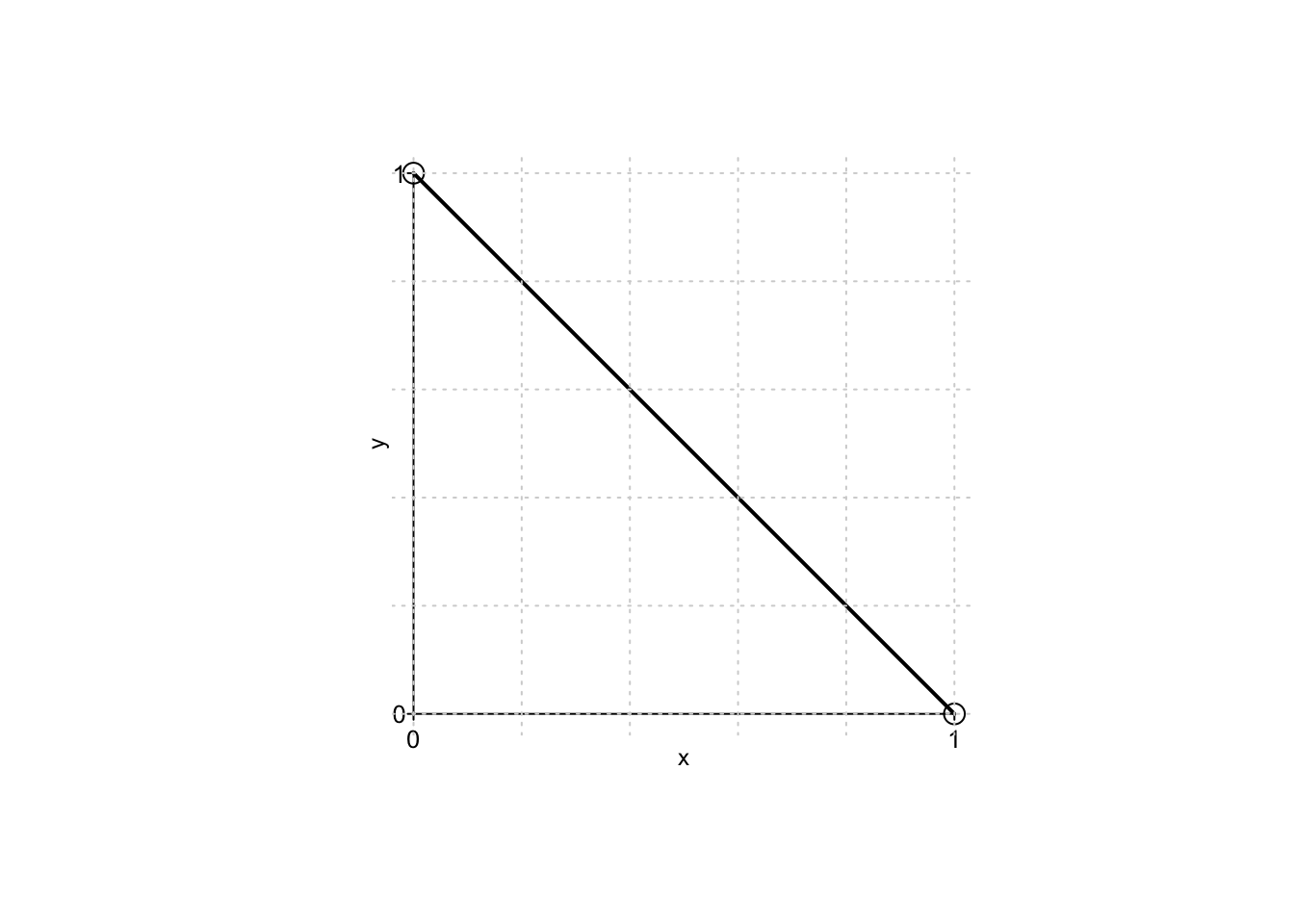 A questo punto basta sostituire una delle due variabili, ad esempio
A questo punto basta sostituire una delle due variabili, ad esempio
In conclusione, tra tutti i rettangoli di (semi-)perimetro fissato, quello avente area massima è il quadrato (
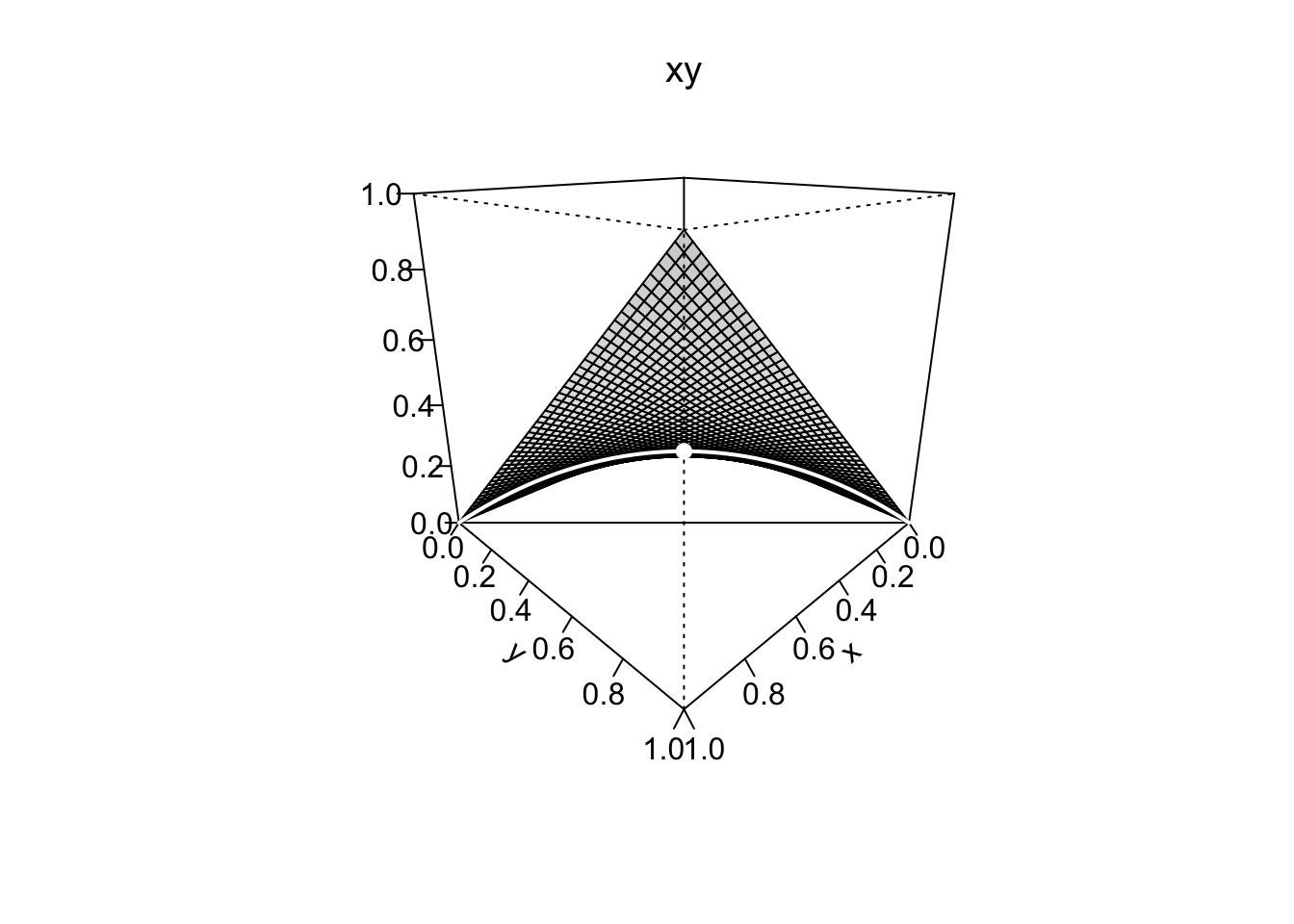
La soluzione nell’Esempio 9.16 corrisponde (con vincoli di non negatività delle variabili) a quella del problema economico di un consumatore con funzione di utilità
che deve scegliere quante unità di un primo bene avente prezzo unitario , e di un secondo bene avente prezzo unitario acquistare sotto il vincolo di bilancio Si veda a questo proposito l’Esempio 9.21.
Example 9.17Tra tutti i rettangoli di area fissata, si determinino quelli aventi semi-perimetro massimo e minimo.
Detti
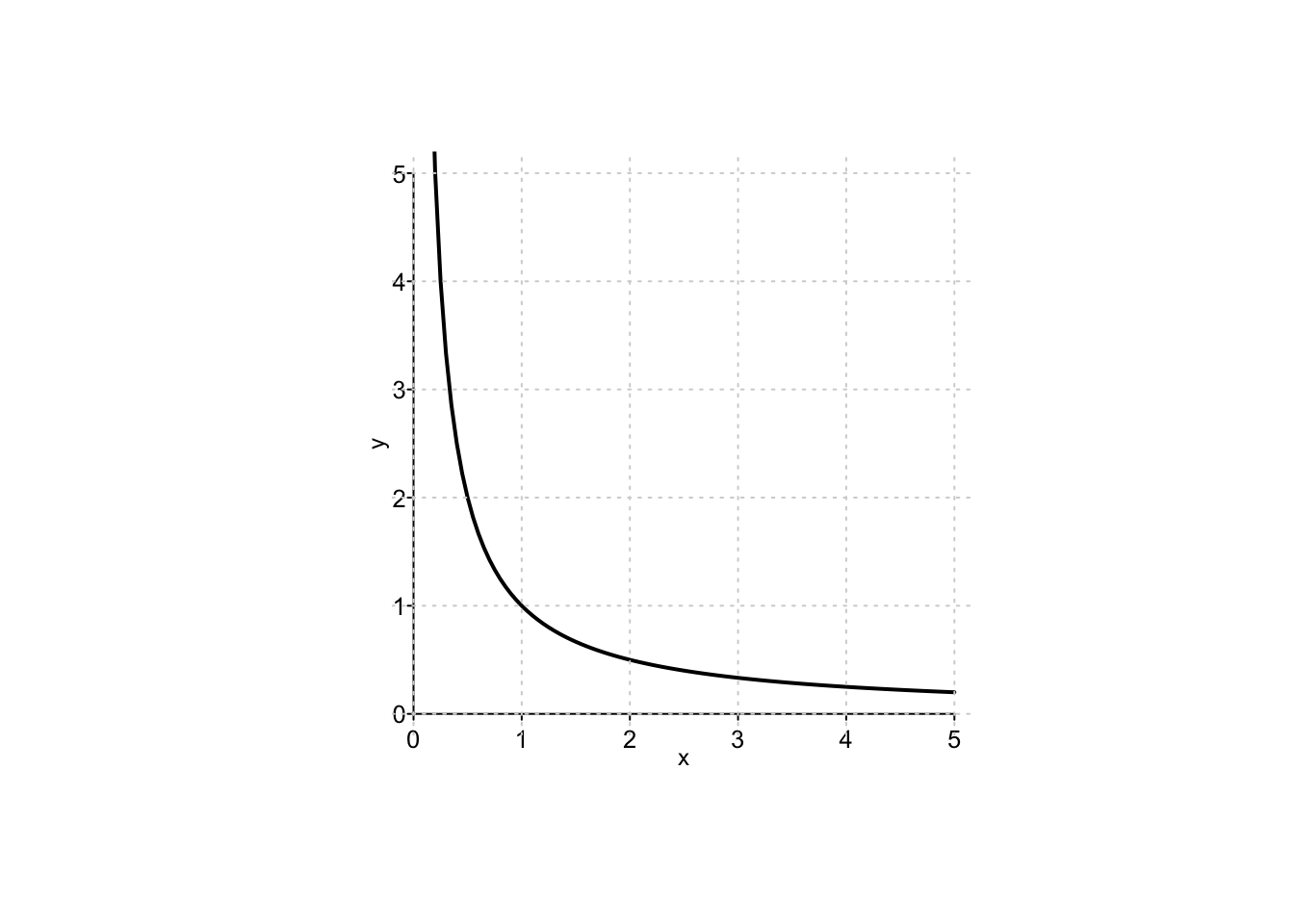 A questo punto basta sostituire una delle due variabili, ad esempio
A questo punto basta sostituire una delle due variabili, ad esempio
In conclusione, la funzione
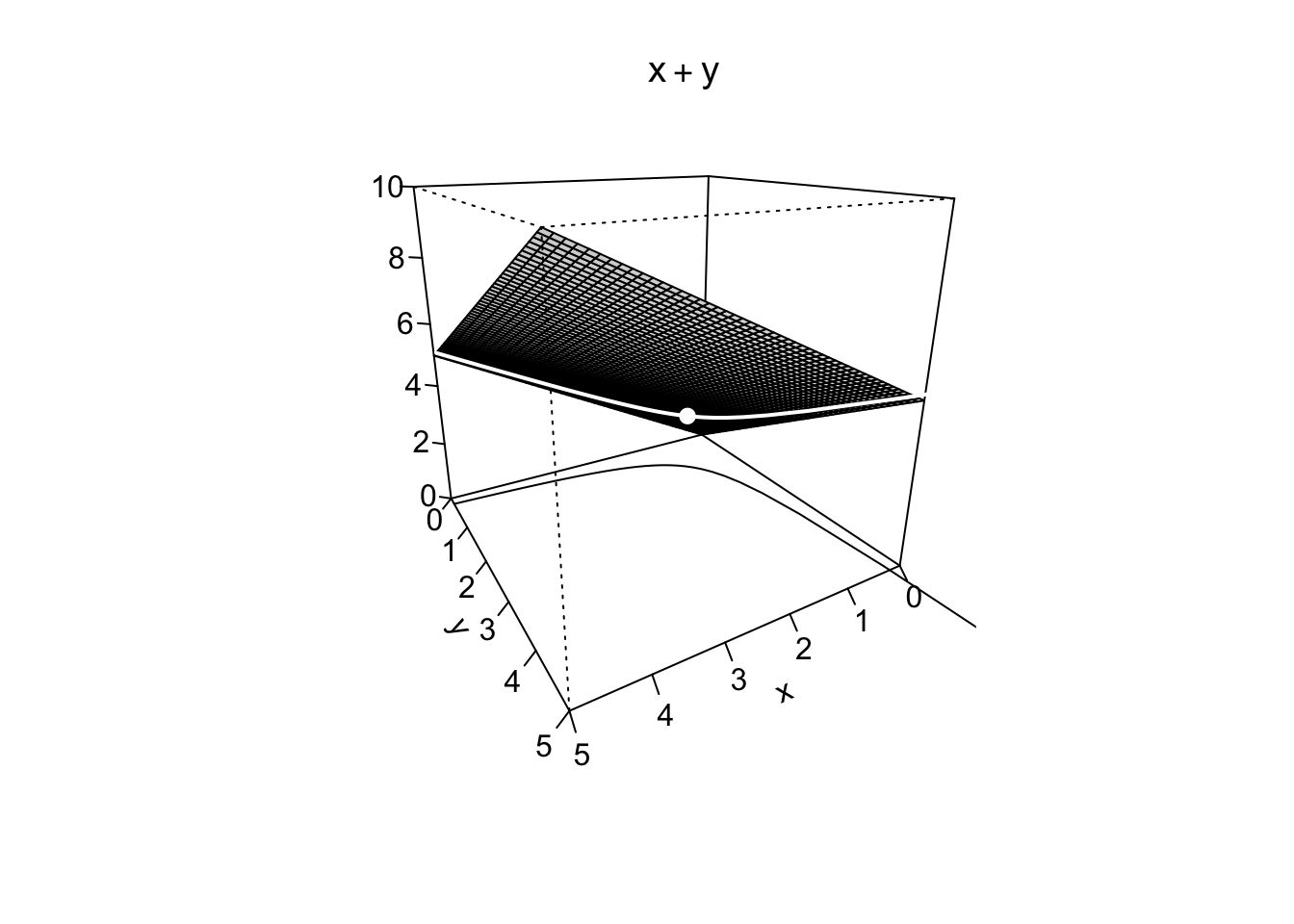
Schema di risoluzione completo di una ottimizzazione su un insieme vincolato con vincoli sostituibili (B):
- si controlla che il vincolo o i vincoli possano essere sostituiti facilmente nella funzione obiettivo (caso B), in modo da ottenere una funzione di una variabile;
- se possibile, si disegna il dominio di ottimizzazione come sottoinsieme del piano cartesiano;
- si effettua la sostituzione più semplice, identificando il dominio di ottimizzazione dove varia la variabile rimanente;
- si risolve il corrispondente problema ad una dimensione.
Example 9.18Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione
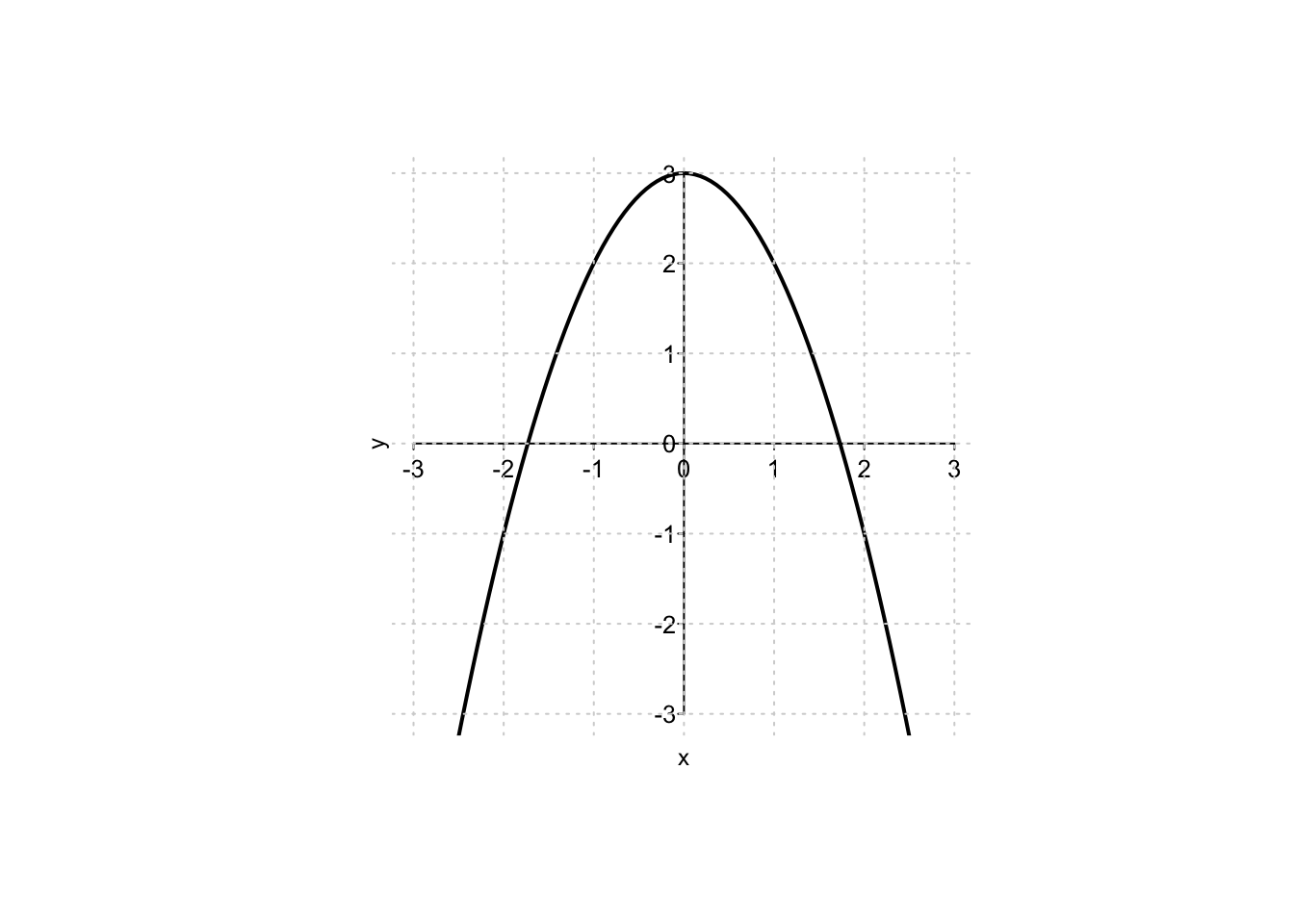
Si osservi che il vincolo può essere sostituito nella funzione. Nel farlo, si deve anche osservare che la sostituzione
In conclusione, la funzione
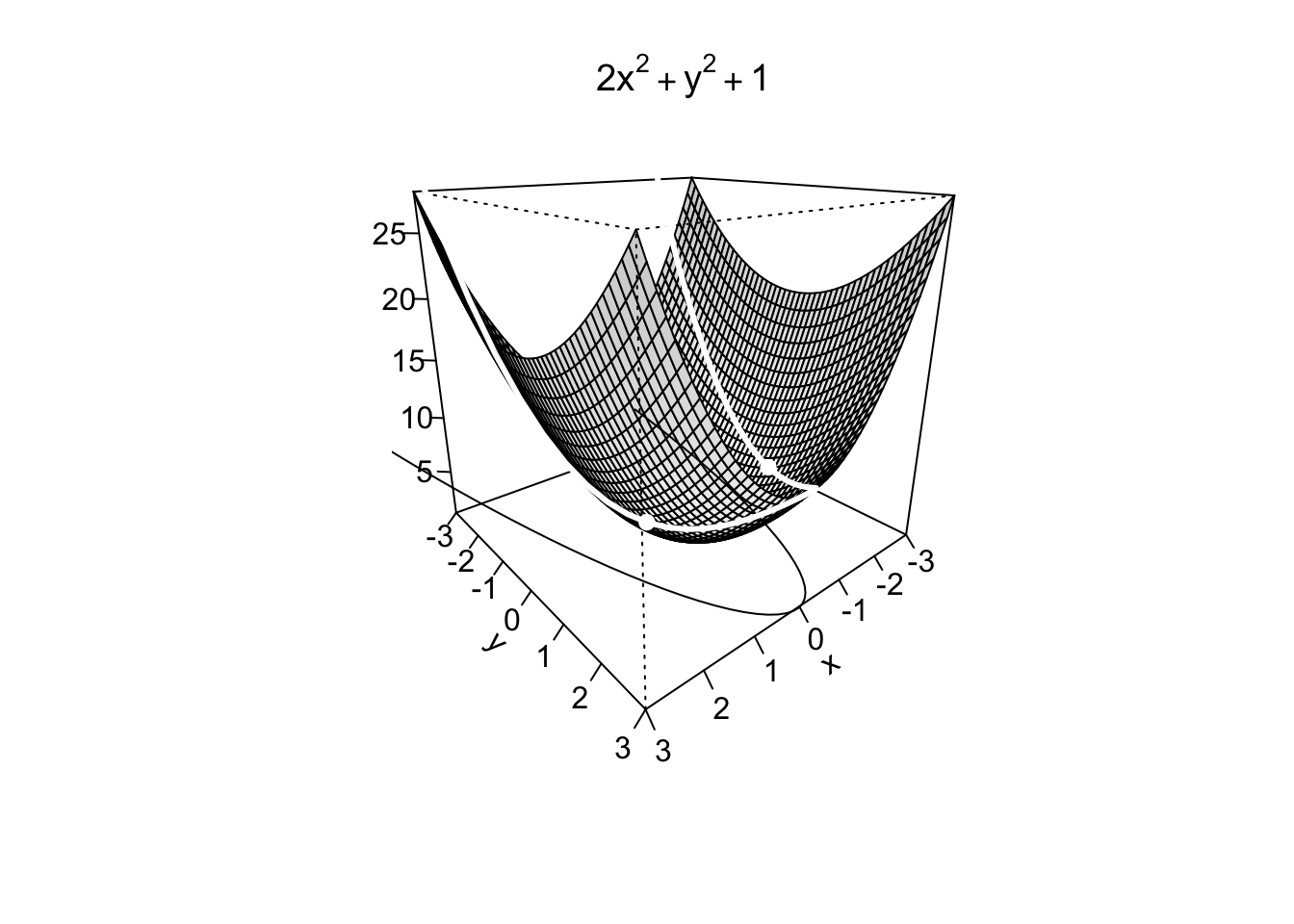
9.7 Il metodo dei moltiplicatori di Lagrange
Nel caso in cui si ottimizzi una funzione su un dominio di ottimizzazione definito da un solo vincolo di uguaglianza, il seguente teorema dà le condizioni necessarie affinché un punto sia di massimo o minimo relativo.
Theorem 9.5 (Teorema dei moltiplicatori di Lagrange)Si assuma che la funzione obiettivo
Remark. Osserviamo i seguenti punti fondamentali sul Teorema dei moltiplicatori di Lagrange:
- la incognita
- il metodo dei moltiplicatori di Lagrange funziona nei punti stazionari trovati se su di essi non si annullano entrambe le derivate parziali
- nel caso in cui l’insieme
- come tutte le condizioni del primo ordine, ovvero basate esclusivamente sulle derivate prime, quelle enunciate nel teorema sono solo necessarie ma non sufficienti a garantire che i punti trovati siano effettivamente di massimo/minimo. È possibile enunciare anche delle condizioni sufficienti del secondo ordine ma esse si basano sulla convessità della funzione lagrangiana, ovvero di una funzione a tre variabili, e quindi vanno oltre gli scopi di questo corso (così come la dimostrazione della validità del metodo dei moltiplicatori);
- come vedremo negli esempi seguenti, trovare i punti stazionari della funzione lagrangiana significa risolvere un sistema (non necessariamente lineare) a tre variabili e tre incognite, per cui non esiste un metodo generale di risoluzione;
- per utilizzare il Teorema, si deve scrivere il vincolo della forma
- in alcuni libri di testo, la funzione lagrangiana è definita come
Come in generale accade per i teoremi basati esclusivamente su derivate del primo ordine, il Teorema dei moltiplicatori di Lagrange dà condizioni solo necessarie per un punto di massimo/minimo. È quindi richiesto uno sforzo aggiuntivo per determinare l’esatta natura dei punti trovati.
In tali casi è utile determinare l’esistenza del massimo/minimo della funzione obiettivo attraverso il Teorema di Weierstrass enunciato nel Capitolo 5, che è valido sotto le stesse ipotesi anche nel caso bivariato. Per enunciarlo in più dimensioni, è sufficiente definire il concetto di insieme limitato.
Definizione 9.10Un insieme
La definizione di insieme limitato è molto semplice ed intuitiva: un insieme è limitato se lo si può racchiudere dentro un cerchio; si veda la figura seguente.
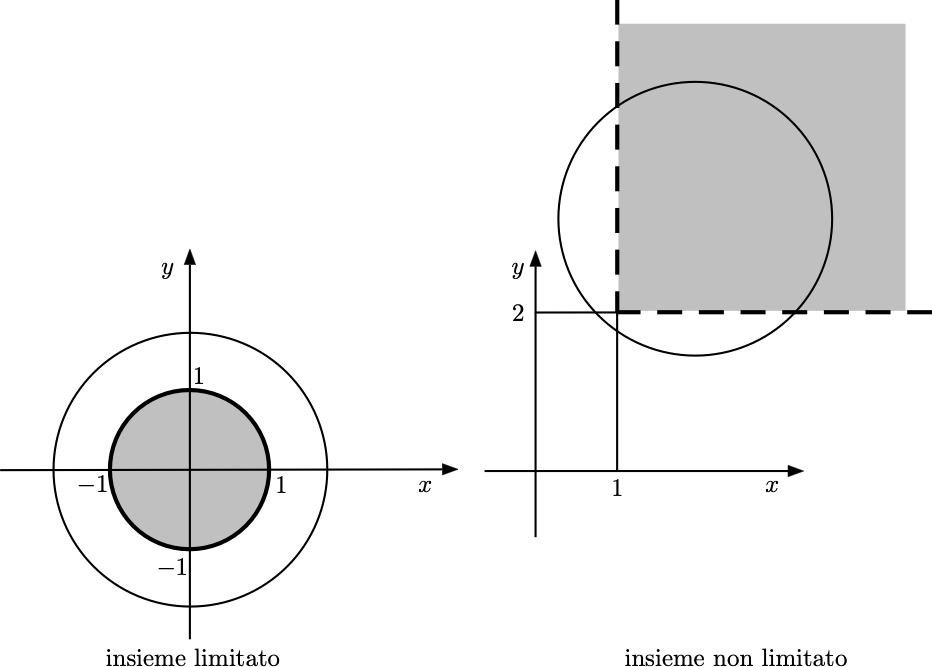
Se riconoscere un insieme limitato è immediato, grazie al seguente teorema è molto semplice anche stabilire quando un insieme è chiuso.
Theorem 9.6Data una funzione continua
Siamo quindi pronti per enunciare il teorema di Weierstrass.
Theorem 9.7 (Teorema di Weierstrass)Una funzione
Si può quindi usare il Teorema dei moltiplicatori di Lagrange in abbinamento col Teorema di Weierstrass per risolvere alcuni problemi di ottimizzazione vincolata, come illustrato negli esempi seguenti.
Example 9.19Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione
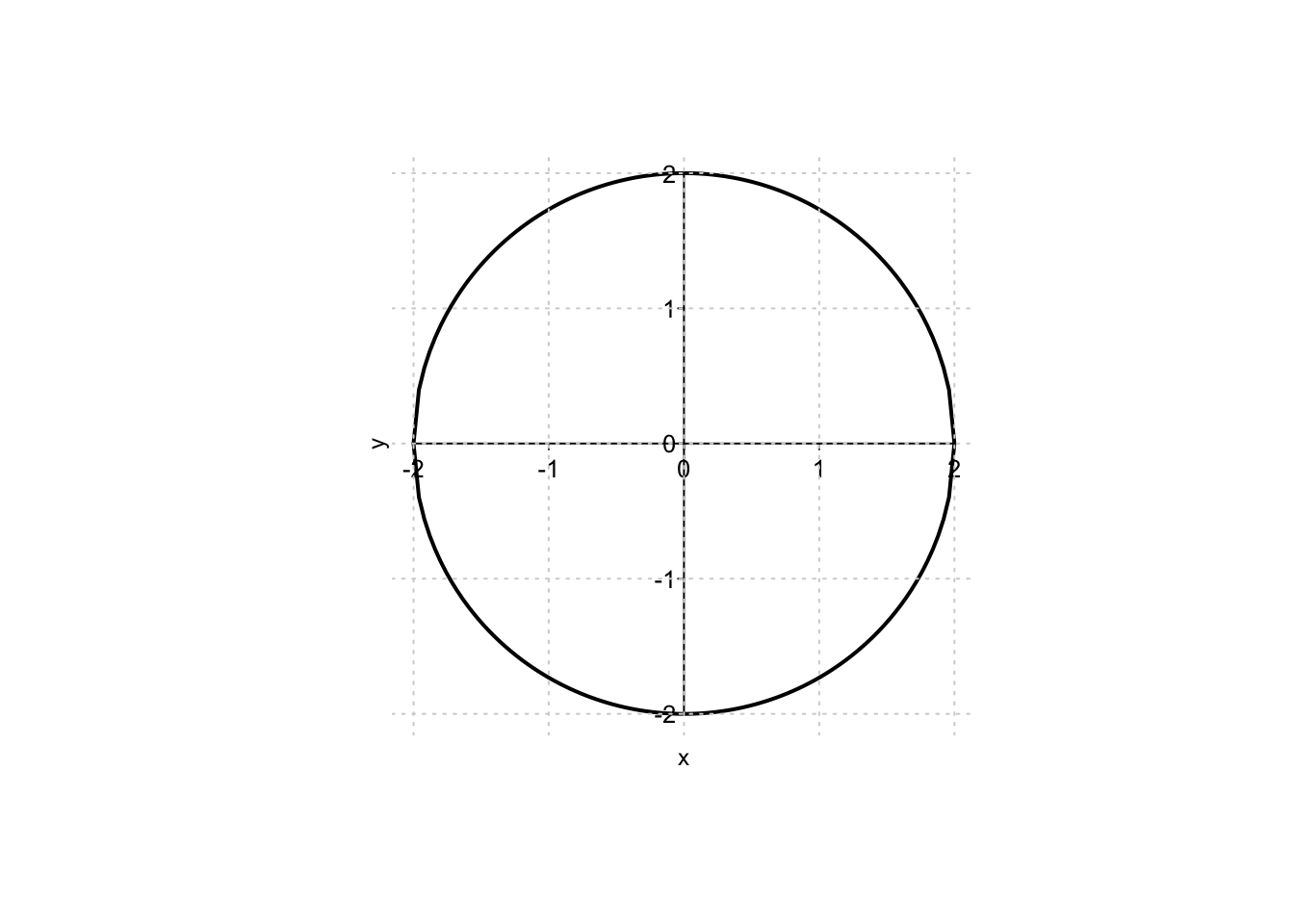
L’insieme
I punti stazionari della funzione lagrangiana
Si osservi che l’ultima equazione del sistema dato dall’annullamento delle derivate parziali della funzione lagrangiana è il vincolo del problema di ottimizzazione.
Pur non esistendo un metodo generale di risoluzione del sistema (9.2), di solito si ricava il moltiplicatore di Lagrange dalle prime due equazioni, e quindi si sostituisce l’equazione trovata nella terza.
Dalle prime due equazioni si osserva che deve necessariamente essere
In conclusione
Schema di risoluzione completo di una ottimizzazione con un vincolo di
- si controlla che il vincolo non sia facilmente sostituibile nella funzione obiettivo, in modo da ottenere una funzione di una variabile (e ricondursi al caso B);
- si controlla la validità del Teorema di Weierstrass (altrimenti non sarà possibile determinare la natura delle soluzioni eventualmente trovate);
- si trovano eventuali punti candidati a punti di massimo/minimo tra i punti stazionari della funzione lagrangiana;
- se la funzione ammette massimo/minimo, si valuta la funzione su tutti i punti candidati: i punti di massimo (minimo) assoluto saranno i punti candidati dove la funzione assume valore più grande (piccolo).
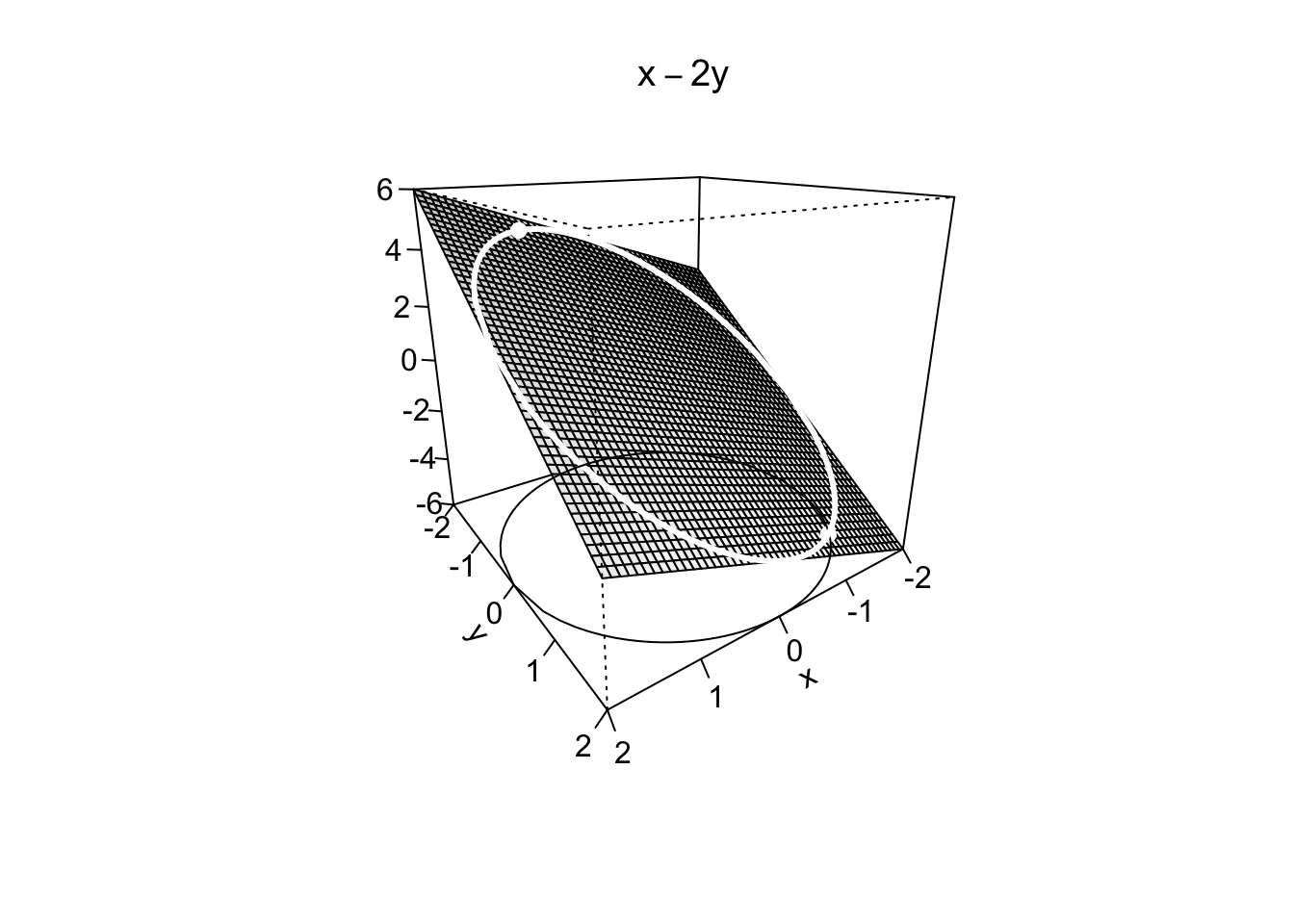
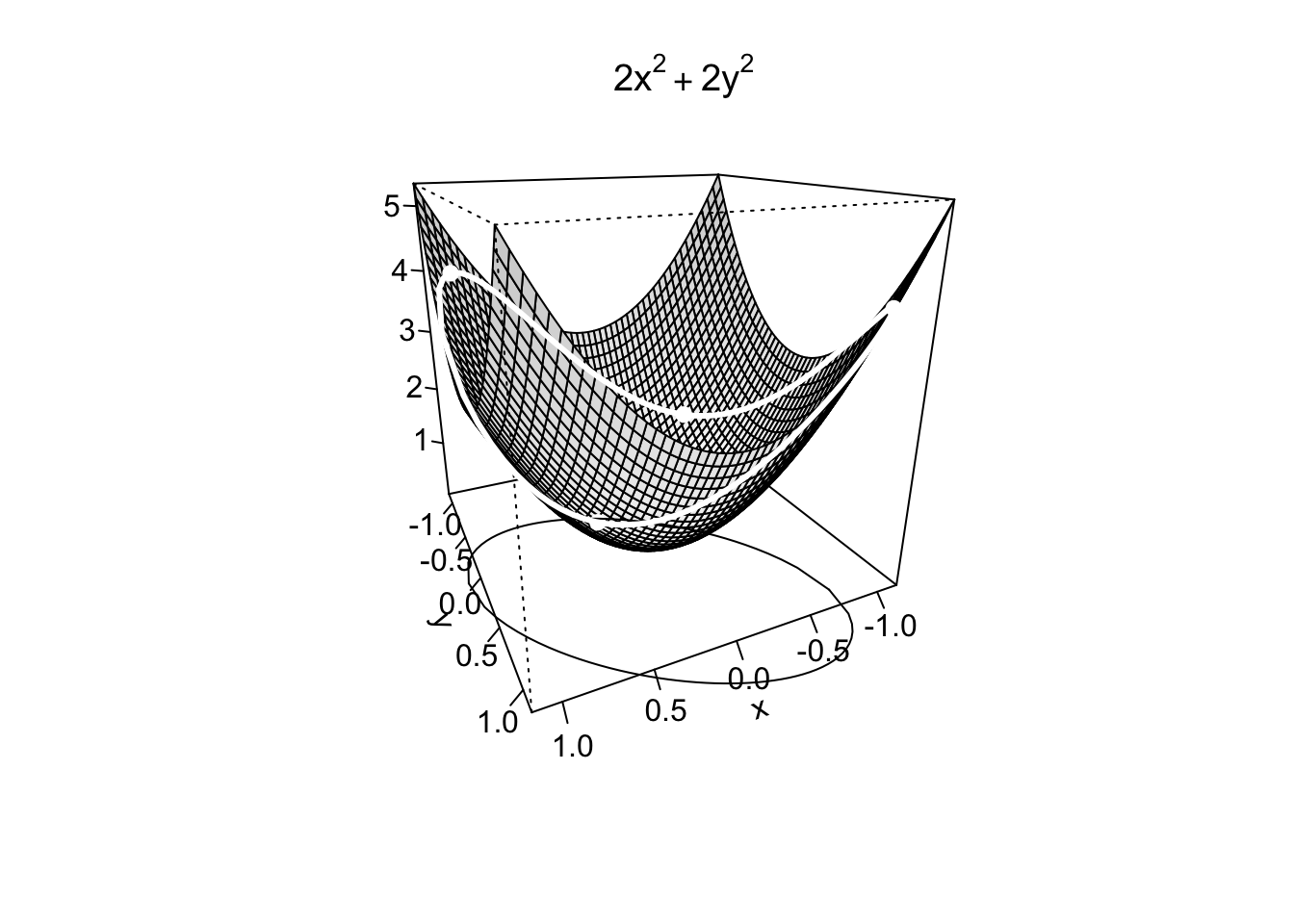
Example 9.20Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione
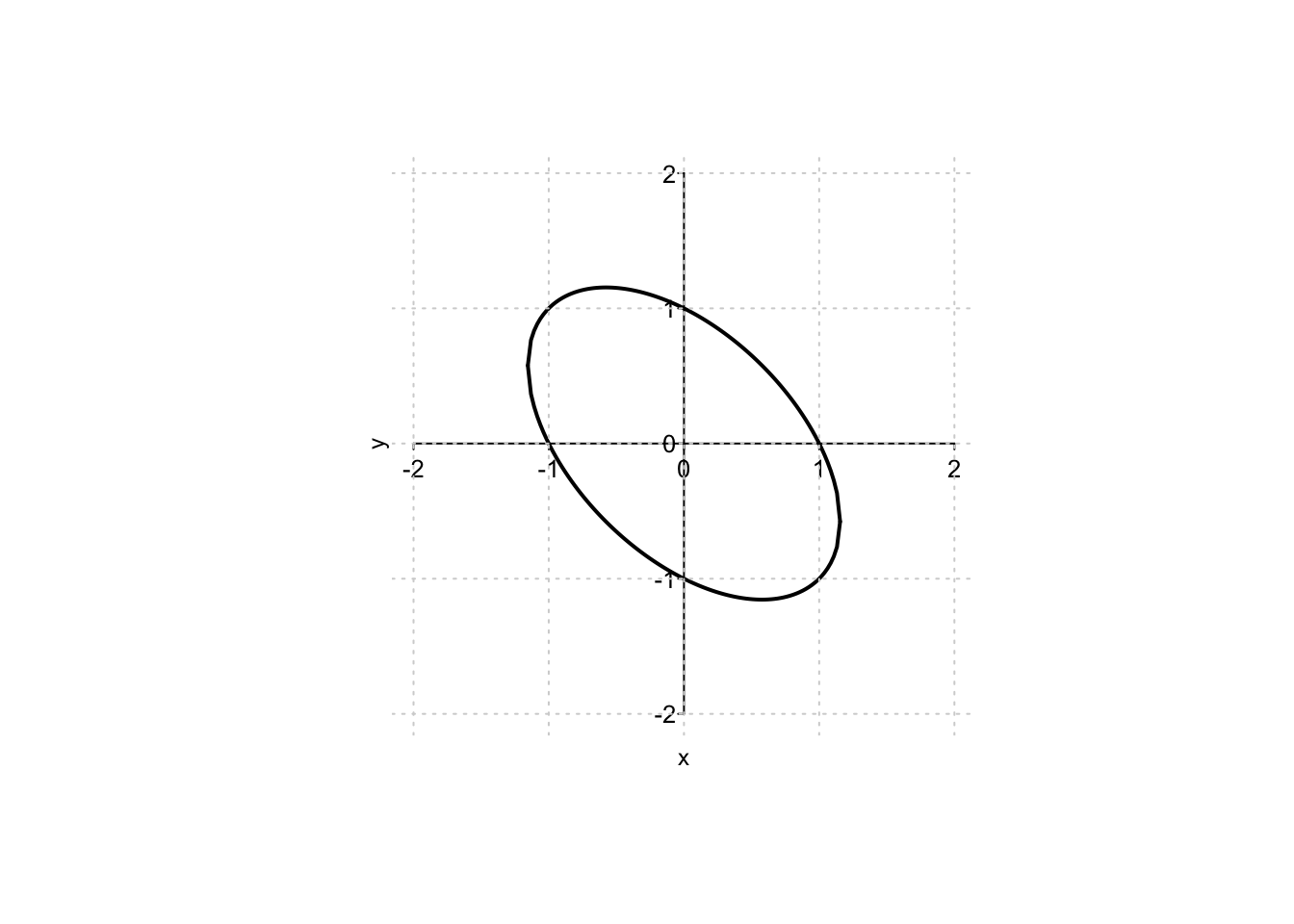 L’equazione che definisce l’ellisse non è di facile sostituzione nella funzione obiettivo per ottenere una funzione univariata, ma si osserva che l’insieme
L’equazione che definisce l’ellisse non è di facile sostituzione nella funzione obiettivo per ottenere una funzione univariata, ma si osserva che l’insieme
I punti stazionari della funzione lagrangiana
Se fosse
Assumendo dunque
- sostituendo nel vincolo
- sostituendo nel vincolo
Dato che massimo e minimo assoluti della funzione esistono per il Teorema di Weierstrass, ed essi devono forzatamente essere raggiunti sui punti candidati, basta valutare la funzione sui punti trovati
Example 9.21Si studi il classico problema economico del consumatore che ha a disposizione una somma
Ricavando il moltiplicatore di Lagrange dalle prime due equazioni, e quindi sostituendo l’equazione così trovata nella terza, si ottiene la condizione necessaria:
Riprendendo l’Esempio 9.16, se
Se
L’unica possibile soluzione del problema vincolato è quindi
9.8 Massimo e minimo su dominio chiuso e limitato
In generale, per quanto riguarda l’ottimizzazione di funzioni di due variabili, si può affermare quanto già detto per le funzioni di una variabile.
Una funzione
- nei punti stazionari interni al suo dominio;
- nei punti di frontiera inclusi nel suo dominio.
Questa affermazione vale in generale per l’ottimizzazione di funzioni di
variabili. Tutti gli schemi di risoluzione trattati in questo capitolo si estendono analogamente per funzioni di variabili con domini di ottimizzazione definiti da un numero finito di vincoli.
Se
L’unica differenza nell’ottimizzazione di funzioni di una variabile o di due variabili è la differente natura dei domini di ottimizzazione: è naturalmente più complesso ottimizzare su un dominio multidimensionale.
Schema di risoluzione completo di ottimizzazione in un dominio chiuso e limitato (definito da più vincoli) (D):
- si controlla la validità del Teorema di Weierstrass per poter stilare una lista di punti candidati tra i quali poter certamente trovare i punti di massimo/minimo;
- si cercano punti candidati a massimo/minimo tra eventuali punti stazionari interni del dominio di ottimizzazione, uguagliando a zero le due derivate parziali della funzione e calcolando la matrice Hessiana per determinare la natura dei punti;
- si cercano altri punti candidati tra i punti di frontiera inclusi nel dominio, riducendo la funzione a univariata o utilizzando il Teorema dei moltiplicatori di Lagrange;
- se la funzione ammette massimo/minimo, si valuta la funzione su tutti i punti candidati: i punti di massimo (minimo) assoluto saranno i punti candidati dove la funzione assume valore più grande (piccolo).
Example 9.22Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione  Si ricercano quindi punti candidati ad essere punti di massimo/minimo nei punti stazionari interni a
Si ricercano quindi punti candidati ad essere punti di massimo/minimo nei punti stazionari interni a
Requisito necessario per calcolare derivate del primo e secondo ordine in un punto è che il punto in questione sia interno al dominio nel quale lo si sta considerando. È quindi un errore grave procedere al calcolo della matrice Hessiana nei punti di frontiera del dominio di ottimizzazione.
I punti di massimo/minimo della funzione sono quindi localizzati sui quattro lati del quadrato
LATO A)
LATO B)
LATO D)
LATO C)
Dato che la funzione ammette massimo e minimo, dalla analisi dei punti candidati risulta in conclusione che la funzione ha punto di massimo assoluto in
A meno che il testo dell’esercizio non lo richieda espressamente, non è necessario calcolare il valore raggiunto dalla funzione nei punti di massimo/minimo.
9.9 Esercizi riassuntivi
In alcuni casi particolari, l’ottimizzazione di una funzione di due variabili può essere semplificata. È quindi sempre raccomandabile studiare il problema in oggetto per trovare la strategia di risoluzione più veloce, e non svolgere meccanicamente i passi descritti in generale.
Example 9.23Si trovino e si classifichino tutti i punti stazionari della funzione
È immediato osservare che la presenza dell’esponenziale, funzione strettamente crescente, naturalmente influenza il massimo/minimo della funzione ma non altera la localizzazione dei punti di massimo/minimo.
Si può quindi considerare la funzione
- se
- se
- nel caso rimanente, ovvero se
Per capire la natura dei quattro punti stazionari trovati, si calcola la matrice Hessiana
In conclusione,
Le stesse conclusioni valgono per
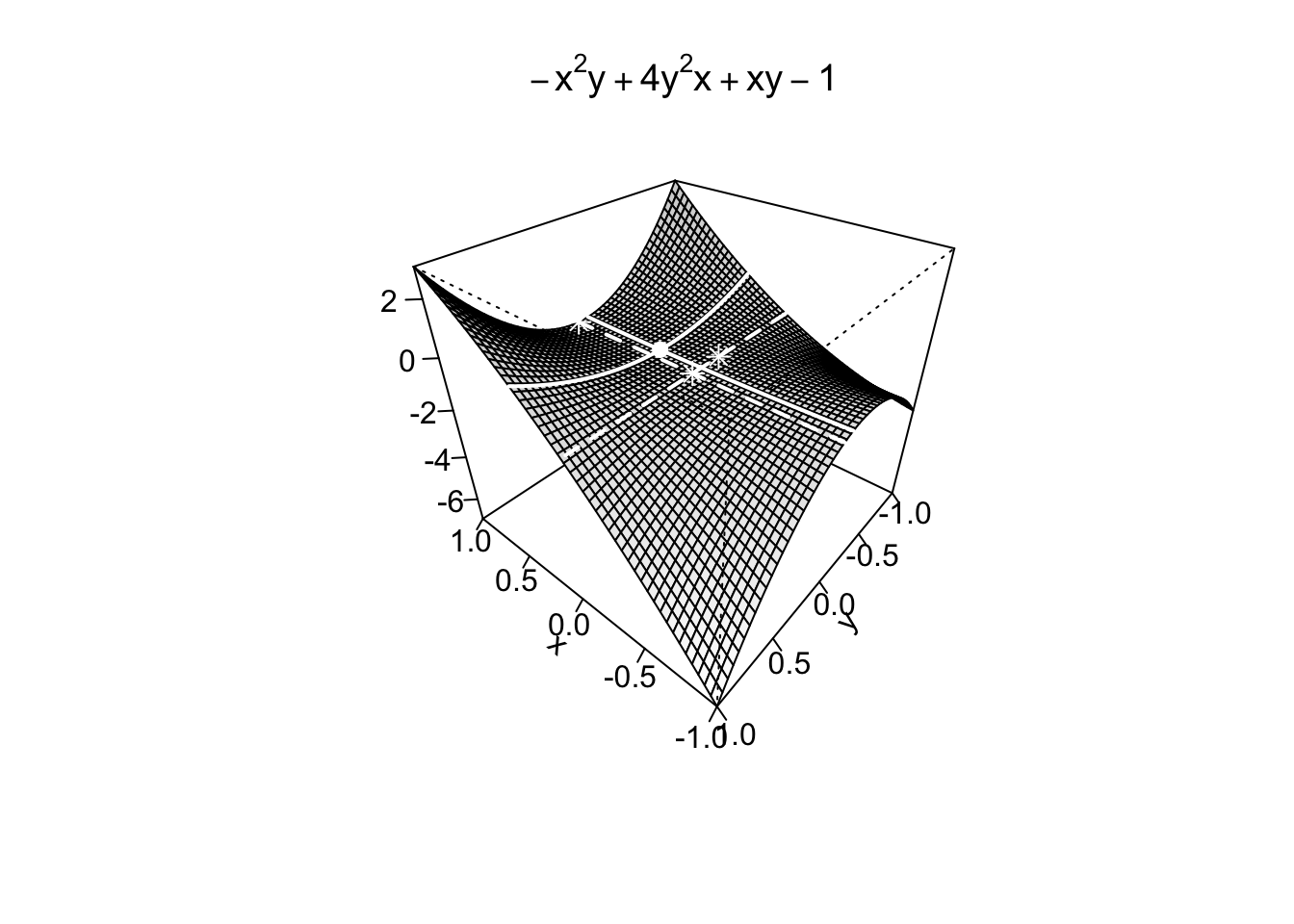
Un altro caso facilmente risolvibile è quello in cui la funzione obiettivo sia a variabili separabili ovvero si possa esprimere come
Example 9.24Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione
È fondamentale osservare che la funzione
Per quanto riguarda
Per quanto riguarda
In conclusione, si ha che
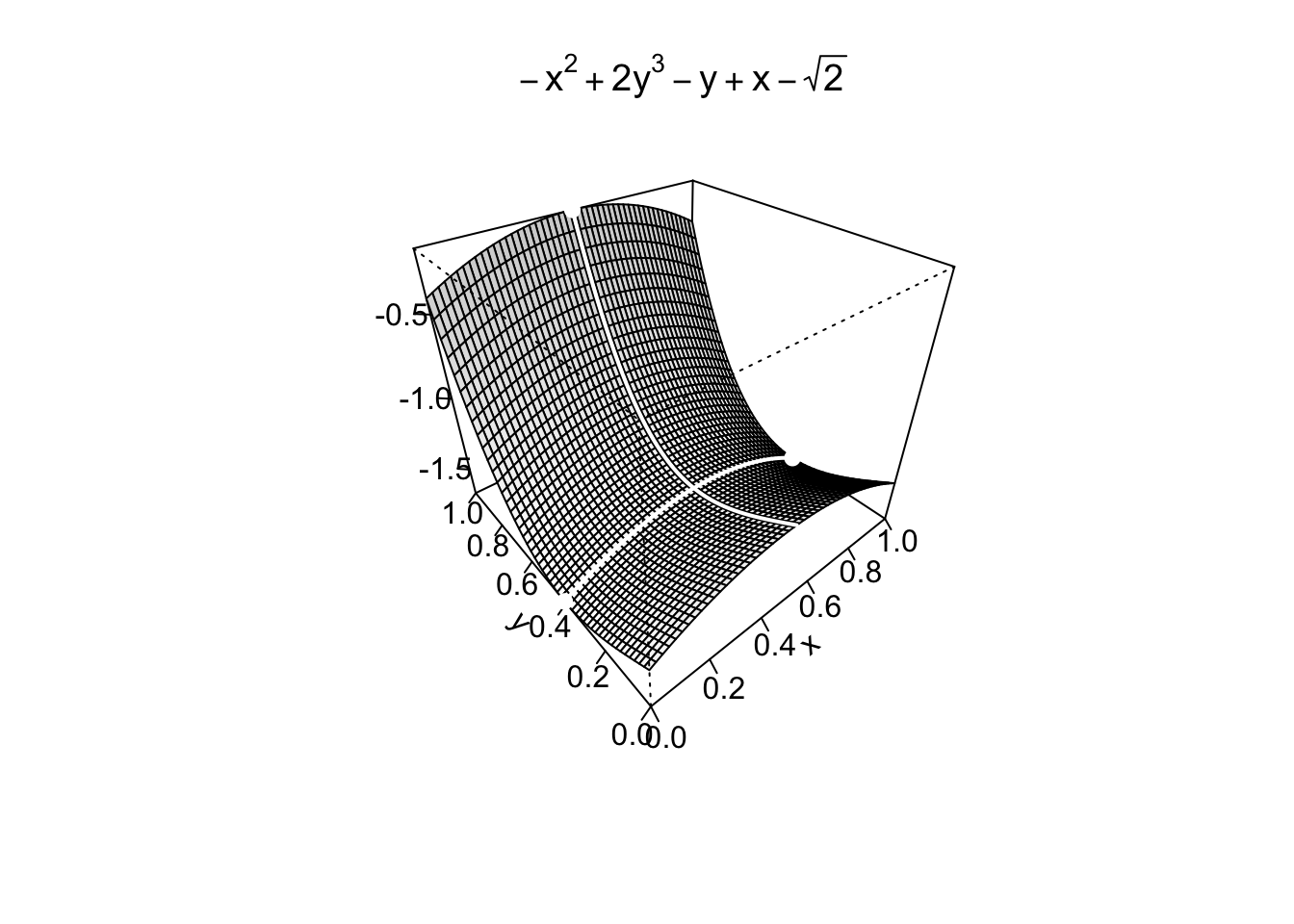
Concludiamo questa sezione con altri due esempi di ottimizzazione.
Example 9.25Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione
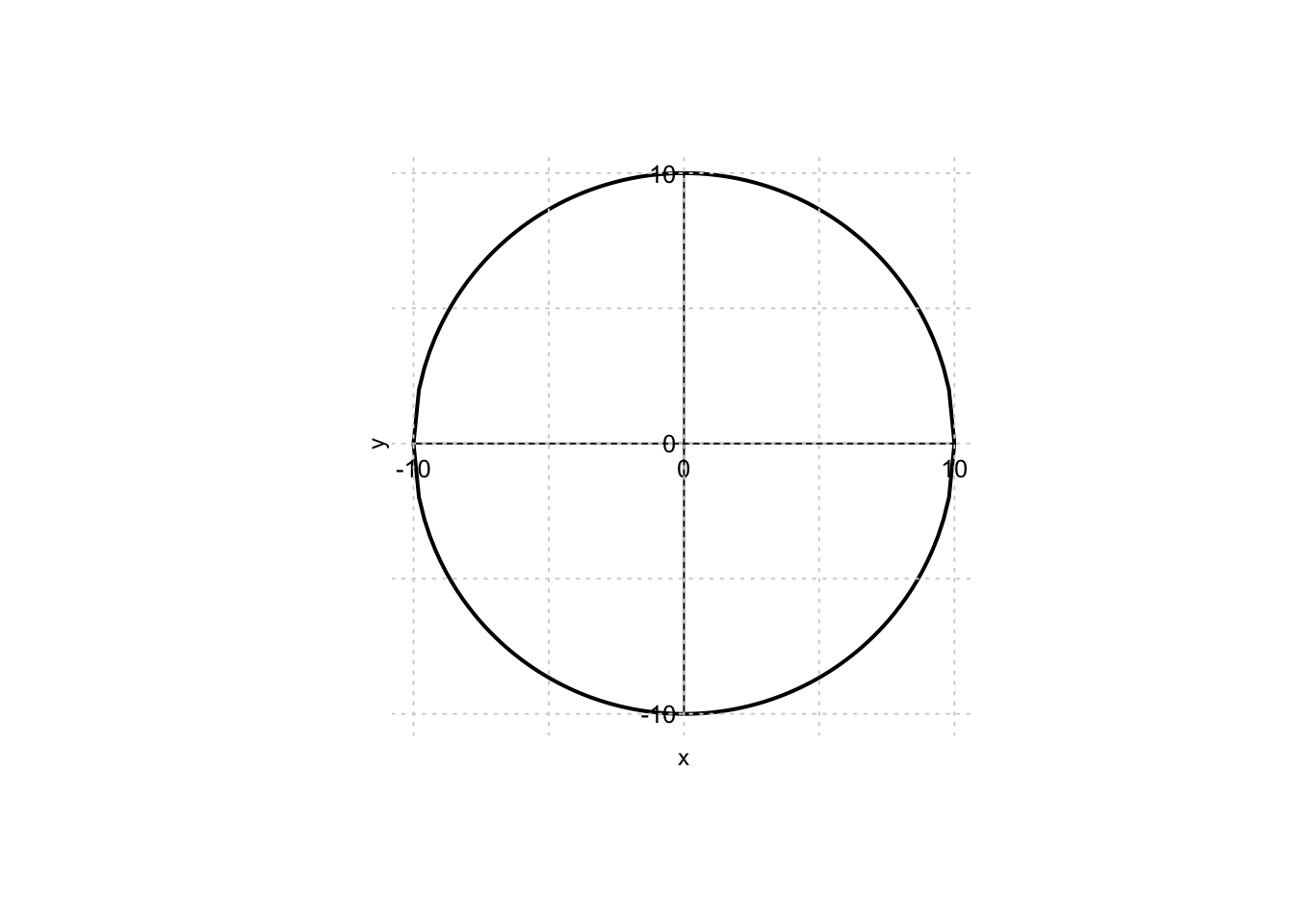
Essendo l’insieme
I punti stazionari della funzione lagrangiana
Dalle prime due equazioni si osserva che deve necessariamente essere
In conclusione
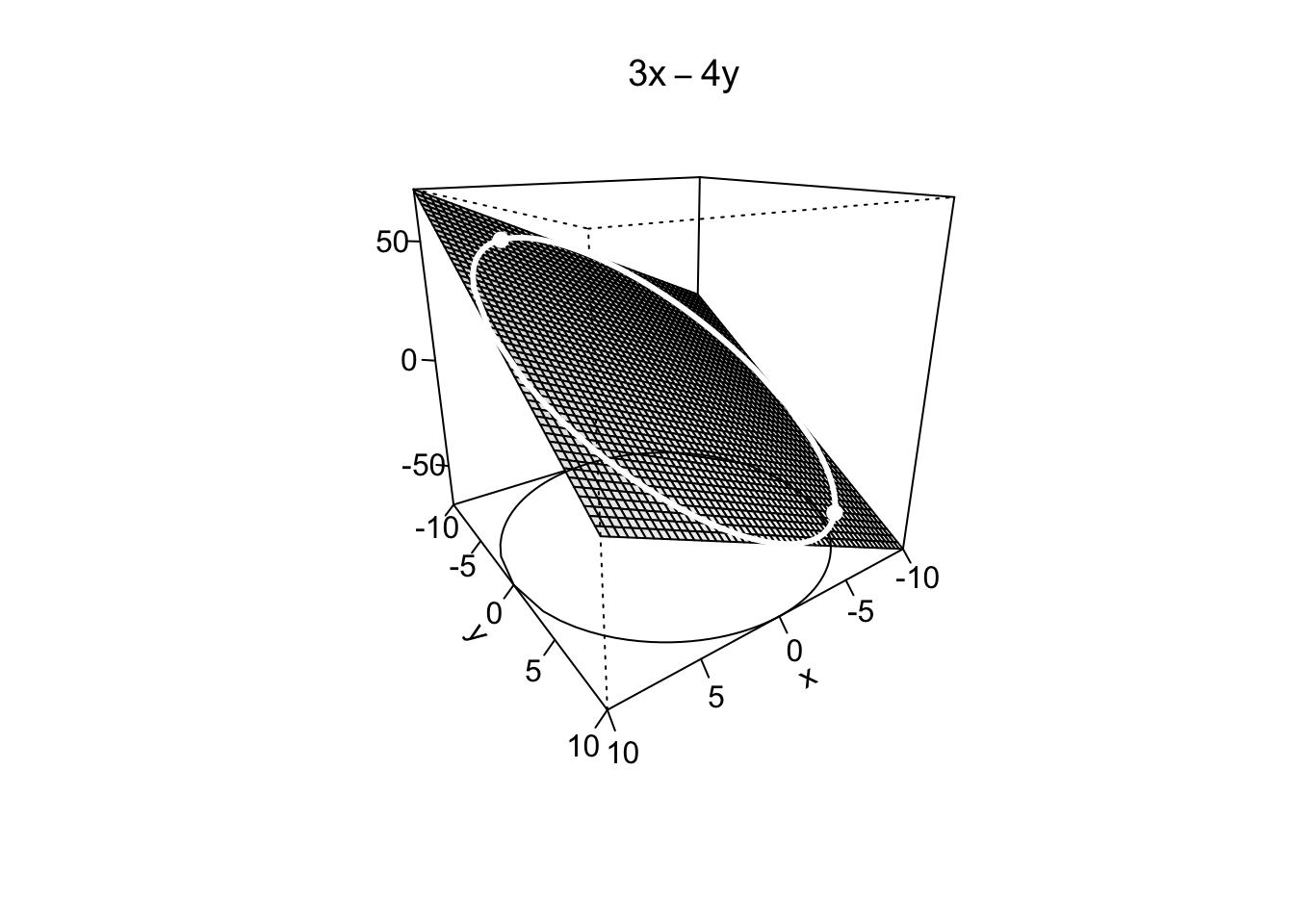
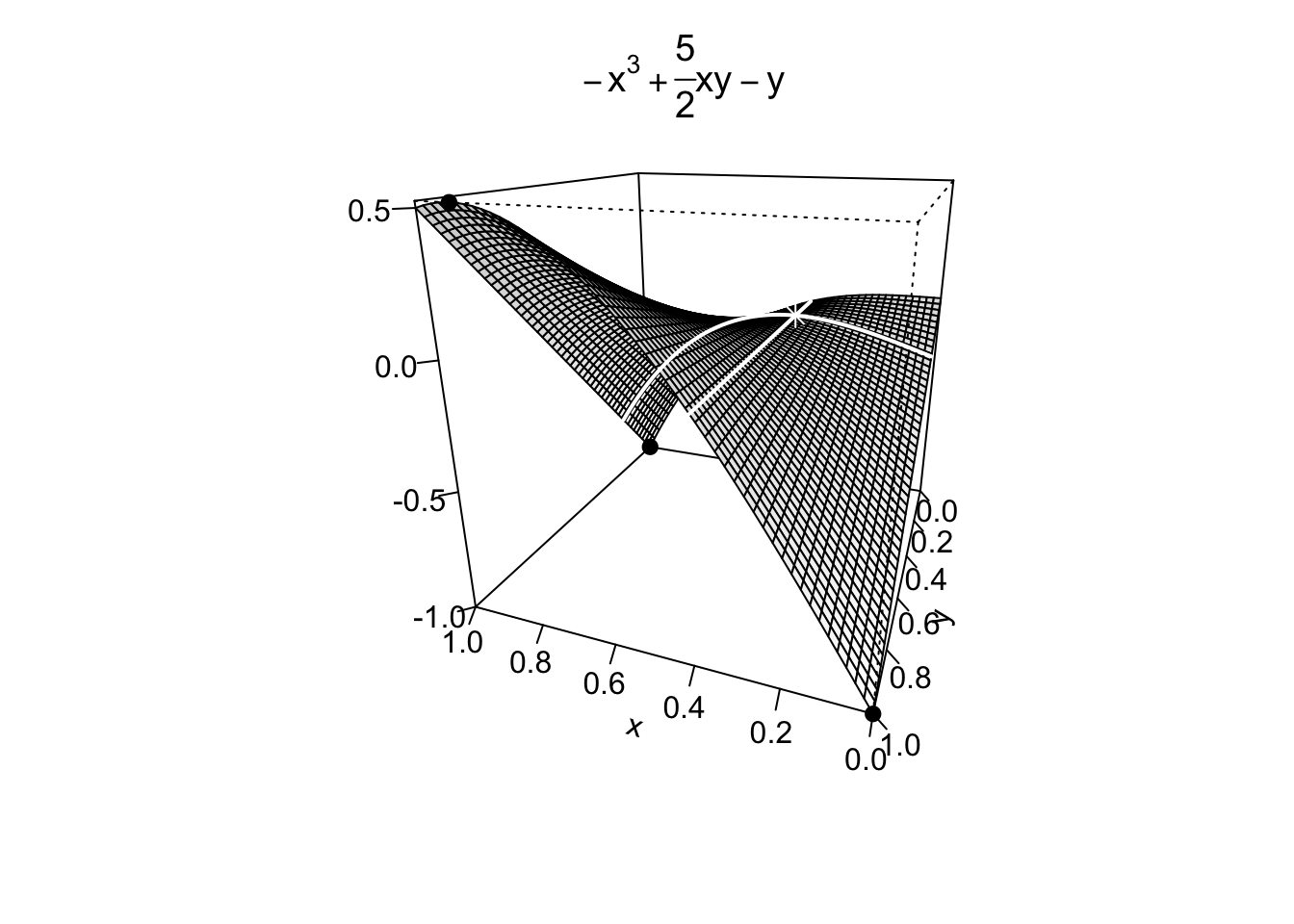
Example 9.26Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione  Si procede quindi come per la tipologia D ricercando punti candidati ad essere punti di massimo/minimo nei punti stazionari interni a
Si procede quindi come per la tipologia D ricercando punti candidati ad essere punti di massimo/minimo nei punti stazionari interni a
I punti di massimo della funzione sono invece localizzati sui quattro lati di
La funzione obiettivo è un polinomio di secondo grado in cui i coefficienti delle variabili di secondo grado sono positivi. Non è necessario quindi svolgere in dettaglio uno studio lato per lato come fatto nell’Esempio 9.22, perché sostituendo un valore qualsiasi ad una delle due variabili
Dato che la funzione ammette massimo e minimo, dalla analisi dei punti candidati risulta in conclusione che la funzione ha punto di massimo assoluto in
9.10 Il modello di regressione lineare
Il modello (di regressione) lineare è uno dei modelli matematici maggiormente utilizzati in Statistica. Il modello si utilizza nell’ipotesi di una relazione di dipendenza funzionale (lineare) tra due variabili, che permetta di prevedere il valore di una in funzione del valore assunto dall’altra.
Si assuma di avere un numero 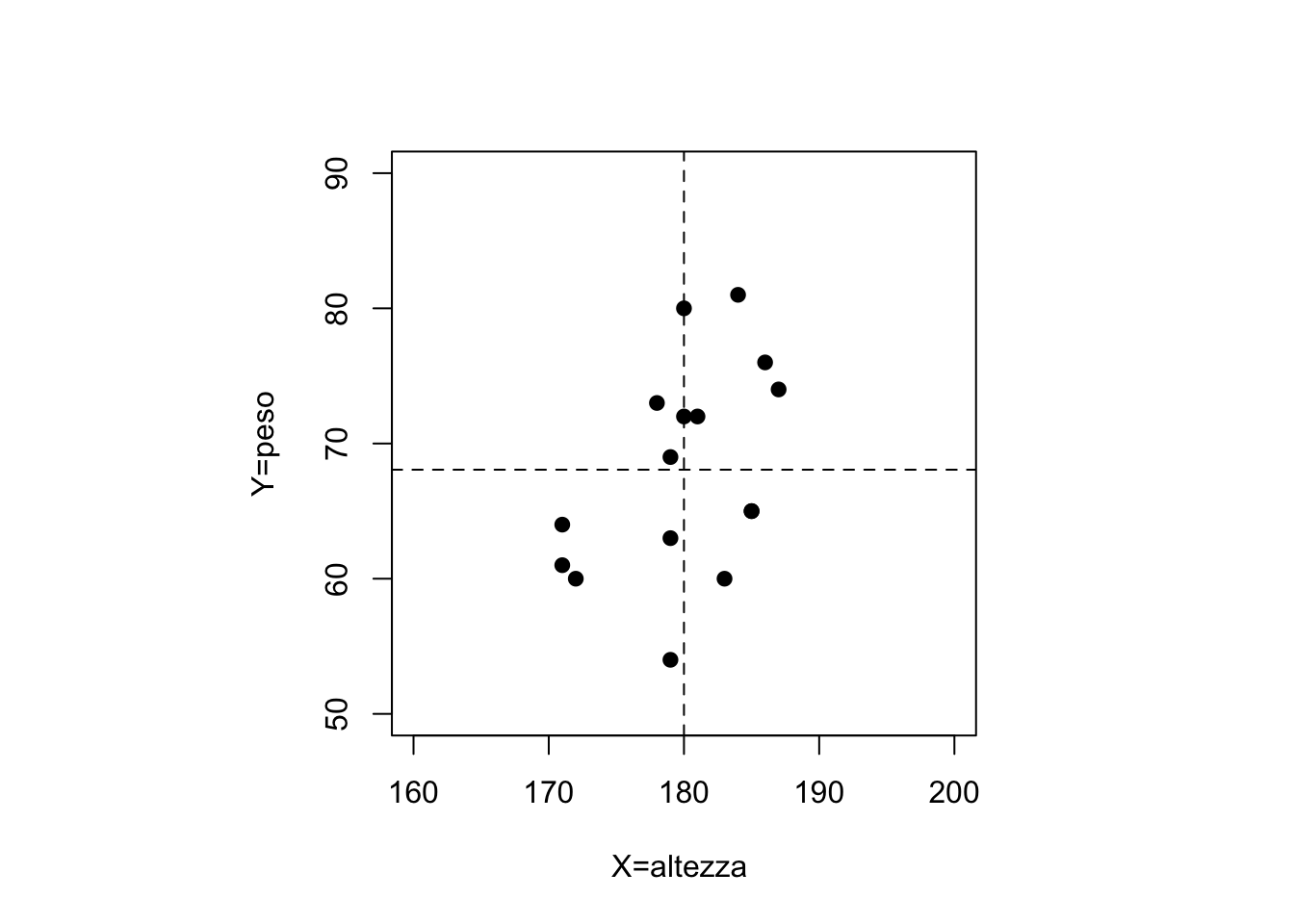
Nel grafico, sono rappresentate anche le medie campionarie delle due variabili, ovvero i valori
Sui dati osservati, il valore predetto dal modello di lineare in corrispondenza della osservazione
Nella pratica, l’errore globalmente commesso dalla retta di regressione viene misurato sommando gli scarti quadratici tra i valori osservati
Il problema di regressione è dunque un problema di ottimizzazione non vincolata di tipo A, per cui un eventuale punto di minimo è da ricercarsi tra i punti stazionari della funzione obiettivo.
Si cercano quindi eventuali punti stazionari della funzione obiettivo calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema:
Analogamente, dividendo per
Per capirne la natura, si calcola la matrice Hessiana
Risulta quindi che il punto stazionario trovato, e determinato dalle equazioni (9.6) e (9.5), è un punto di minimo assoluto per
#Dati riguardanti peso e altezza di n persone h=c(186,181,171,178,172,179,179,180,187,179,185,171,184,180,185,183) w=c(76,72,64,73,60,54,69,80,74,63,65,61,81,72,65,60) #Grafico delle osservazioni mh=min(h,160) Mh=max(h,200) mw=min(w,50) Mw=max(w,90) par(mfrow=c(1,1), pty="s") plot(h,w,xlab="altezza",ylab="peso",pch=19,xlim=c(mh,Mh),ylim=c(mw,Mw)) #Nel grafico vengono riportati i valori medi delle osservazioni abline(v=mean(h),lty =2,lwd = 1) abline(h=mean(w),lty =2,lwd = 1) #calcolo modello di regressione lineare reg=lm(w~h) #retta di regressione abline(reg)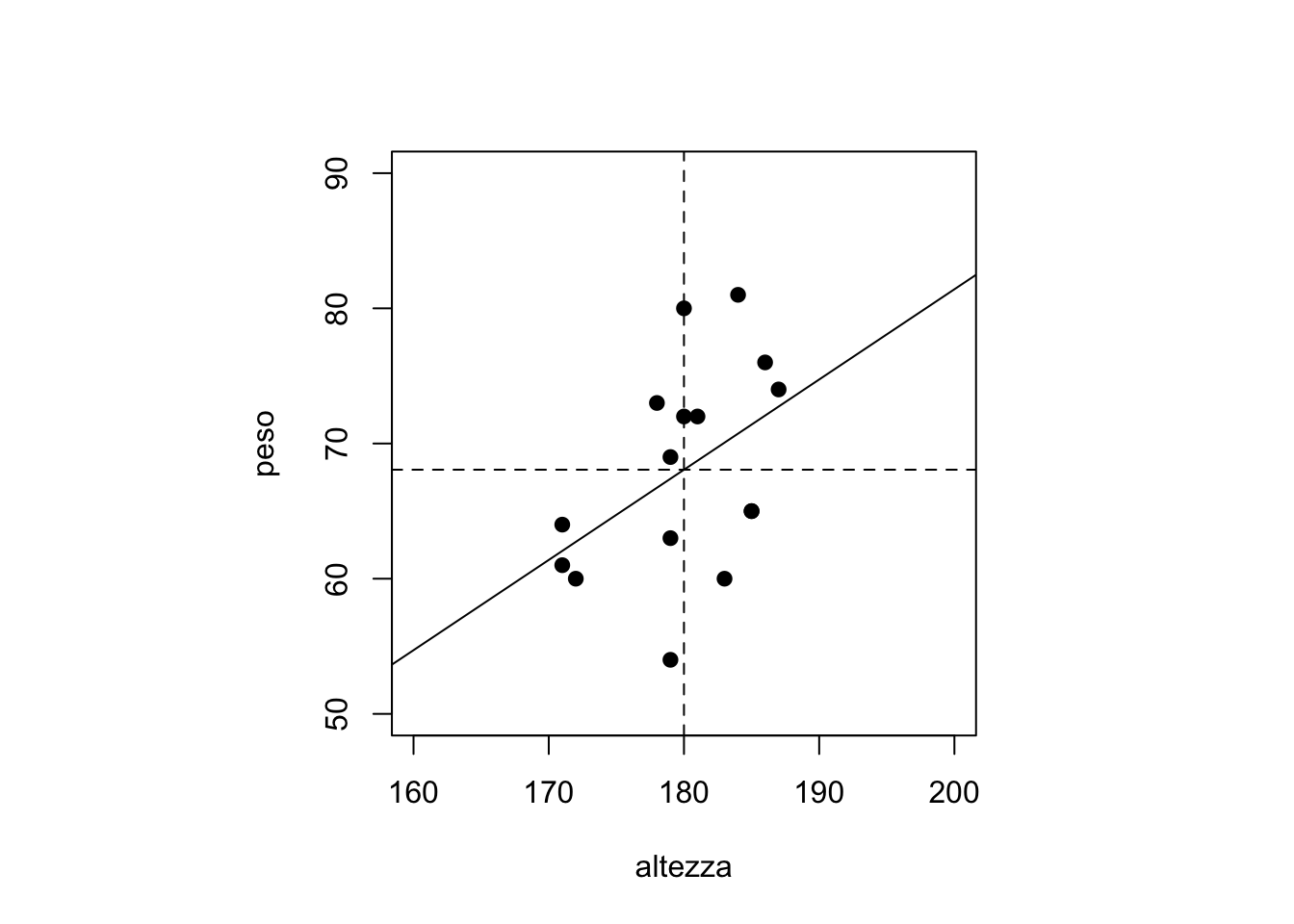
#parametri stimati reg$coefficients## (Intercept) h ## -52.0897843 0.6675127È possibile sfruttare il calcolo matriciale introdotto nel Capitolo 8 per scrivere in modo molto più elegante e conciso il modello di regressione.
Si definiscano le matrici
Osservando che
9.11 Esercizi
Exercise 9.1Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione
Exercise 9.2
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione
Exercise 9.3
Si determinino e classifichino i punti stazionari della funzione
Exercise 9.4
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione
Exercise 9.5
Si dica se esistono e nel caso si trovino massimo/minimo assoluti della funzione
Exercise 9.6
Classificare la natura di tutti i punti stazionari della funzione
Exercise 9.7
Si dica se esistono e nel caso si determinino massimo/minimo assoluti della funzione
Exercise 9.8
Indicare la natura degli eventuali punti stazionari della funzione
Exercise 9.9
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione
Exercise 9.10
Si determinino e classifichino i punti stazionari della funzione
Exercise 9.11
Trovare e classificare i punti stazionari della funzione
Exercise 9.12
Classificare la natura di tutti i punti stazionari della funzione
Exercise 9.13
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione
Exercise 9.14
Si dica se esistono e nel caso si determinino massimo/minimo assoluti della funzione
Exercise 9.15
Classificare la natura di tutti i punti stazionari della funzione
Exercise 9.16
Classificare la natura di tutti i punti stazionari della funzione
Exercise 9.17
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione
