9 Ottimizzazione bivariata
In questo capitolo studieremo come trovare i punti di massimo e di minimo di una funzione di due variabili. Per farlo, generalizzeremo tutti i concetti che ci hanno permesso di studiare le funzioni di una variabile, rendendoli idonei ad essere trattati su un dominio a due dimensioni.
9.1 Funzioni reali di due variabili
L’oggetto di studio di questo capitolo sono le funzioni del tipo \(f: A \subseteq \mathbb{R}^2 \to \mathbb{R}\), ovvero le funzioni aventi come dominio \(A\) un sottoinsieme di \[ \mathbb{R}^2=\mathbb{R}\times \mathbb{R}=\left\{(x,y): x \in \mathbb{R},\, y \in \mathbb{R}\right\}, \] l’insieme delle coppie ordinate \((x,y)\), dove \(x\) e \(y\) sono due numeri reali. Parleremo quindi di funzioni reali di due variabili, in quanto è necessario specificare le due variabili \(x,y\) per determinare il valore (reale) \(f(x,y)\) della funzione.
Anche una funzione reale di due variabili \(f: A \subseteq \mathbb{R}^2 \to \mathbb{R}\) viene usualmente visualizzata attraverso il suo grafico, ovvero attraverso l’insieme \[ \mathcal{G}_f=\{(x,y,f(x,y)) \in \mathbb{R}^3:\, (x,y) \in A\}. \] Si osservi che il grafico di una funzione di due variabili è un sottoinsieme dello spazio \[ \mathbb{R}^3=(\mathbb{R}^2)\times \mathbb{R}, \] e quindi deve essere rappresentato in tre dimensioni. Ne consegue che disegnare il grafico (tridimensionale) di una funzione di due variabili risulta molto più complesso rispetto a disegnare il grafico (bidimensionale) di una funzione di una variabile, ed è per questo che nel seguito ci limiteremo a cercare di ottimizzarla.
Per un insieme a due dimensioni, è necessario dare una nuova definizione di intorno di un punto.
Definition 9.1 Si dice intorno del punto \((x_0,y_0) \in \mathbb{R}^2\) (di raggio \(r>0\)) l’insieme di tutti i punti che distano da \((x_0,y_0)\) meno di \(r\), ovvero il cerchio (circonferenza esclusa) di centro \((x_0,y_0)\) e raggio \(r\): \[ I(x_0,y_0)=I_r(x_0,y_0)=\left\{(x,y) \in \mathbb{R}^2: (x-x_0)^2+(y-y_0)^2<r^2 \right\}. \]
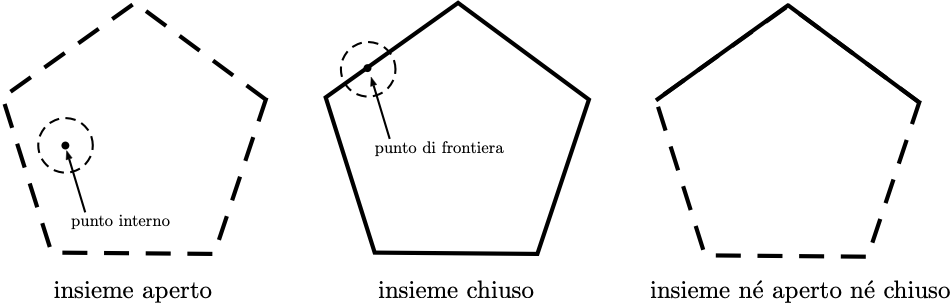
Data la definizione di intorno, tutte le definizioni topologiche viste nel Capitolo 1 quali quelle di punto interno, punto di frontiera, punto di accumulazione, insieme aperto ed insieme chiuso, restano invariate. Nella figura seguente possiamo quindi apprezzare la differenza tra un sottoinsieme aperto di \(\mathbb{R}^2\) (in cui tutti i punti sono interni, a sinistra), un sottoinsieme chiuso (il cui complementare è aperto, al centro), ed uno né aperto né chiuso (a destra). Un insieme chiuso contiene tutti i suoi punti di accumulazione, ovvero contiene il suo “bordo”.
Il nuovo concetto di intorno permette di estendere direttamente le definizioni di limite (ci limitiamo al concetto di limite nell’intorno di un punto) e continuità di una funzione.
Definition 9.2 Siano dati la funzione \(f:A \subseteq \mathbb{R}^2 \to \mathbb{R}\), e \((x_0,y_0) \in \mathbb{R}^2\) punto di accumulazione per \(A\). Si dice che il limite di \(f\) per \((x,y)\) che tende a \((x_0,y_0)\) è uguale ad \(L\in \mathbb{R^*}\) e si scrive \[ \lim_{(x,y) \to (x_0,y_0)} f(x,y) =L, \] se per qualsiasi intorno \(I(L)\) di \(L\), è possibile trovare un intorno \(I(x_0,y_0)\) tale che: \[\begin{equation*} \text{ per ogni } (x,y) \in A \cap I(x_0,y_0)\setminus\{(x_0,y_0)\}, \text{ si ha che } f(x,y) \in I(L). \end{equation*}\]
Definition 9.3 Una funzione \(f:A \subseteq \mathbb{R}^2 \to \mathbb{R}\) si dice continua nel punto \((x_0,y_0) \in A\) se \[ \lim_{(x,y) \to (x_0,y_0)} f(x,y) =f(x_0,y_0). \] Se \(f\) è continua in ogni \((x_0,y_0) \in A\), si dice che \(f\) è continua su \(A\).
Analogamente al caso univariato (unidimensionale), segue nel caso bivariato (bidimensio-nale) che:
tutte le funzioni che tratteremo nel seguito di questo capitolo sono continue sul loro dominio naturale;
la somma, differenza, quoziente, composizione di funzioni continue, laddove correttamente definite, sono continue sul loro dominio naturale.
Per le funzioni di due variabili, il dominio naturale viene definito in modo completamente analogo alle funzioni di una variabile.
Definition 9.4 Per una funzione \(f:D_f \subseteq \mathbb{R}^2\to \mathbb{R}\) definita dall’espressione analitica \((x,y) \to f(x,y)\), l’insieme \(D_f\) è detto dominio naturale di \(f\) se esso è il più grande sottoinsieme di \(\mathbb{R}^2\) in cui \(f(x,y)\) è correttamente definita.
Analogamente al caso unidimensionale, un restringimento del dominio naturale di una funzione può essere causato da:
la presenza di una frazione, in cui il denominatore deve essere non nullo;
la presenza di una radice quadrata, il cui argomento deve essere non negativo;
la presenza di un logaritmo, il cui argomento deve essere positivo.
Per una funzione a due variabili, il dominio naturale (essendo un sottoinsieme di \(\mathbb{R}^2\)) può essere raffigurato sul piano cartesiano. La rappresentazione del dominio non deve essere confusa con il grafico della funzione, che è invece tridimensionale e quindi dovrà essere raffigurato in tre dimensioni.
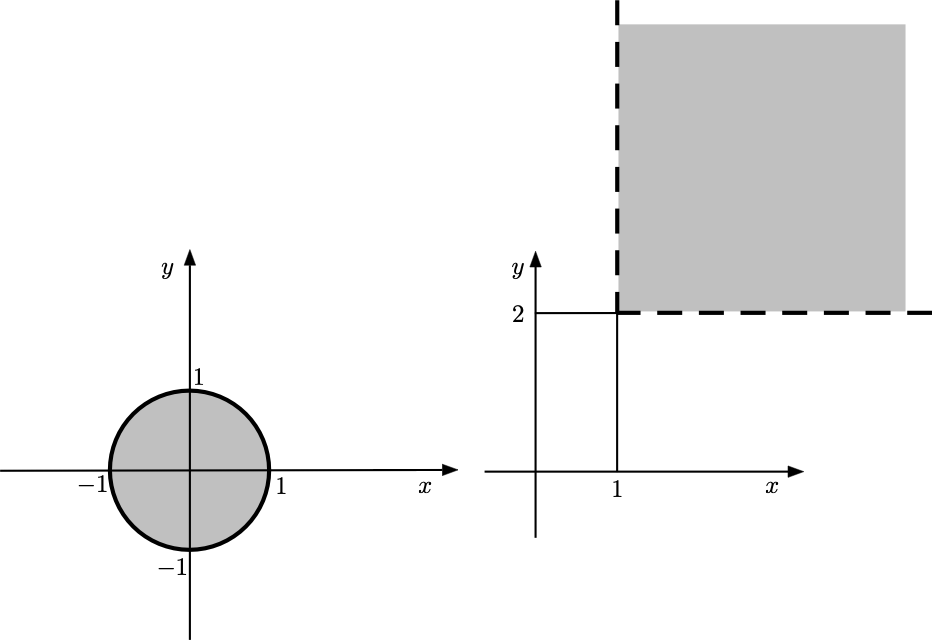
Example 9.1 Si trovi il dominio naturale della funzione \(f:D_f \subseteq \mathbb{R}^2 \to \mathbb{R},\) definita da \[ f(x,y)=\sqrt{1-x^2-y^2}. \] Data la presenza della radice, si deve imporre che \(1-x^2-y^2\geq 0\), ovvero il dominio naturale è dato da \[ D_f=\{(x,y) \in \mathbb{R}^2: x^2+y^2 \leq 1\}. \] Sul piano cartesiano, l’insieme \(D_f\) è rappresentabile come il cerchio (circonferenza compresa) di centro l’origine e raggio unitario. Il dominio (che è un insieme chiuso) è raffigurato nel piano cartesiano nella seguente figura, a sinistra.
Example 9.2 Si trovi il dominio naturale della funzione \(f:D_f\subseteq \mathbb{R}^2 \to \mathbb{R},\) definita da \[ f(x,y)=\log \, (x-1) + \log\, (y-2). \] Data la presenza dei logaritmi, si deve imporre che \(x-1>0\) e \(y-2>0\), ovvero il dominio naturale è dato da \[ D_f=\{(x,y) \in \mathbb{R}^2: x>1,\,y>2\}. \] Il dominio (che è un insieme aperto) è raffigurato nel piano cartesiano nella seguente figura, a destra.
9.2 Derivate parziali del primo ordine
Analogamente al caso univariato, il calcolo delle derivate si rivelerà strumento essenziale per l’ottimizzazione di una funzione bivariata.
Il concetto di derivata per una funzione di due variabili viene definito nel modo più semplice ed intuitivo possibile: se si fissa una variabile nella funzione \(f(x,y)\), prendendo \(y=y_0\) ad esempio, si ottiene la funzione \(f(x,y_0)\) di una variabile, per cui è già stato definito nel Capitolo 4 cosa si intende per derivata. Allo stesso modo, se si pone \(x=x_0\), si potrà derivare la funzione di una variabile \(f(x_0,y)\). Operando in questo modo, si ottengono due derivate che sono dette derivate parziali.
Definition 9.5 Data la \(f:A \subseteq \mathbb{R}^2\to \mathbb{R},\, (x,y) \to f(x,y),\) si dice:
derivata parziale rispetto alla prima variabile (rispetto a \(x\)), nel punto interno \((x,y) \in A\), il limite \[ \frac{\partial f}{\partial x}(x,y)=\lim_{h \to 0 } \,\frac{f(x+h,y)-f(x,y)}{h}, \] se quest’ultimo esiste finito;
derivata parziale rispetto alla seconda variabile (rispetto a \(y\)), nel punto interno \((x,y) \in A\), il limite \[ \frac{\partial f}{\partial y}(x,y)=\lim_{h \to 0 } \,\frac{f(x,y+h)-f(x,y)}{h}, \] se quest’ultimo esiste finito.
Nel caso esistano le due derivate parziali, esse si dicono derivate del primo ordine.
Quando esiste, la derivata parziale \(\frac{\partial f}{\partial x}(x,y)\) si calcola fissando il valore della \(y\) e derivando la funzione rispetto a \(x\) (assumendo quindi \(y\) costante); la derivata parziale \(\frac{\partial f}{\partial y}(x,y)\) si calcola analogamente fissando il valore della \(x\) e derivando la funzione rispetto a \(y\) (assumendo quindi \(x\) costante). Si deduce quindi che si è già in grado di calcolare le derivate parziali di una funzione di due variabili perché esse non sono altro che le derivate delle funzioni di una variabile ottenute fissando prima la \(y\), e poi la \(x\).
Per semplicità di notazione, scriveremo \(\frac{\partial f}{\partial x}(x,y)=\frac{\partial f}{\partial x}\) e \(\frac{\partial f}{\partial y}(x,y)=\frac{\partial f}{\partial y}\) nel seguito.
Example 9.3 Si calcolino le derivate parziali della funzione \(f:D_f\subseteq \mathbb{R}^2 \to \mathbb{R}\), definita da \[ f(x,y)=x^2y^3+xy^2+3x^2+2y-4. \]
Si osservi prima di tutto che, essendo la funzione un polinomio (una somma del prodotto di potenze in \(x\) e in \(y\)), il suo dominio naturale è l’insieme \(\mathbb{R}^2\).
Assumendo costante la \(y\), e derivando rispetto a \(x\), si calcola: \[ \frac{\partial f}{\partial x}=2xy^3+y^2+6x. \] Assumendo costante la \(x\), e derivando rispetto a \(y\), si calcola: \[ \frac{\partial f}{\partial y}=3x^2y^2+2xy+2. \]
Example 9.4 Si calcolino le derivate parziali della funzione \(f:D_f\subseteq \mathbb{R}^2 \to \mathbb{R}\), definita da \[ f(x,y)=x^2e^y-3y^3+xy+2. \] Si osservi che si ha \(D_f=\mathbb{R}^2\).
Assumendo costante la \(y\), e derivando rispetto a \(x\), si calcola: \[ \frac{\partial f}{\partial x}=2xe^y+y. \] Assumendo costante la \(x\), e derivando rispetto a \(y\), si calcola: \[ \frac{\partial f}{\partial y}=x^2e^y-9y^2+x. \]
Example 9.5 Si calcolino le derivate parziali della funzione \(f:D_f\subseteq \mathbb{R}^2 \to \mathbb{R}\), definita da \[ f(x,y)=1+2\log (xy) -4 x^2y^2. \]
Prima di tutto è necessario richiedere che l’argomento del logaritmo sia positivo, quindi \[ D_f=\{(x,y) \in \mathbb{R}^2: xy>0\}. \] Assumendo costante la \(y\), e derivando rispetto a \(x\), si calcola: \[ \frac{\partial f}{\partial x}=\frac{2y}{xy}-8xy^2=\frac2x-8xy^2. \] Assumendo costante la \(x\), e derivando rispetto a \(y\), si calcola: \[ \frac{\partial f}{\partial y}=\frac{2x}{xy}-8x^2y=\frac2y-8x^2y. \] Si osservi che le derivate parziali sono ben definite poiché sul dominio naturale della funzione si ha \(x,y \neq 0\).
9.3 Derivate del secondo ordine e matrice Hessiana
Dato che le derivate parziali di una funzione a due variabili sono a loro volta funzioni di due variabili, è naturalmente possibile definire le derivate parziali delle derivate parziali, che prenderanno il nome di derivate parziali del secondo ordine.
Nel caso i corrispondenti limiti esistano finiti, si hanno dunque quattro derivate:
la derivata di \(\frac{\partial f}{\partial x}\) rispetto (ancora) alla variabile \(x\), che si indica, omettendo l’indicazione delle variabili \((x,y)\), con \[ \frac{\partial^2 f}{\partial x^2}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right); \]
la derivata (mista) di \(\frac{\partial f}{\partial x}\) rispetto alla variabile \(y\), che si indica con \[ \frac{\partial^2 f}{\partial y \partial x}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right); \]
la derivata (mista) di \(\frac{\partial f}{\partial y}\) rispetto alla variabile \(x\), che si indica con \[ \frac{\partial^2 f}{\partial x \partial y}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right); \]
la derivata di \(\frac{\partial f}{\partial y}\) rispetto (ancora) alla variabile \(y\), che si indica con \[ \frac{\partial^2 f}{\partial y^2}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right). \]
Nel caso esistano, le quattro derivate del secondo ordine della funzione \(f(x,y)\) vengono raccolte nella cosiddetta matrice Hessiana: \[\begin{equation} H_f(x,y)=\left(\begin{array}{cc}\frac{\partial^2 f}{\partial x^2}(x,y) & \frac{\partial^2 f}{\partial y \partial x}(x,y) \\ \frac{\partial^2 f}{\partial x \partial y}(x,y)& \frac{\partial^2 f}{\partial y^2}(x,y)\end{array}\right). \tag{9.1} \end{equation}\]
Calcolare la matrice Hessiana di una funzione non comporta nessuna difficoltà aggiuntiva rispetto a quanto fatto sino a questo punto, tranne il fatto di dover calcolare quattro nuove derivate di funzioni di una variabile. Calcoliamo quindi la matrice Hessiana negli esempi precedenti.
Example 9.6 Riprendendo l’Esempio 9.3, si calcoli la matrice Hessiana della funzione \(f:\mathbb{R}^2 \to \mathbb{R}\), definita da \[ f(x,y)=x^2y^3+xy^2+3x^2+2y-4. \] Ricordando che \[ \frac{\partial f}{\partial x}=2xy^3+y^2+6x, \] si calcola \[ \frac{\partial^2 f}{\partial x^2}=2y^3+6, \quad \frac{\partial^2 f}{\partial y \partial x}=6xy^2+2y. \]
Ricordando che \[ \frac{\partial f}{\partial y}=3x^2y^2+2xy+2, \] si calcola \[ \frac{\partial^2 f}{\partial x \partial y}=6xy^2+2y, \quad \frac{\partial^2 f}{\partial y^2}=6x^2y+2x. \] Si ottiene quindi la matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}2y^3+6 & 6xy^2+2y \\6xy^2+2y & 6x^2y+2x\end{array}\right). \]
Example 9.7 Riprendendo l’Esempio 9.4, si calcoli la matrice Hessiana della funzione \(f:\mathbb{R}^2 \to \mathbb{R}\), definita da \[ f(x,y)=x^2e^y-3y^3+xy+2. \] Ricordando che \[ \frac{\partial f}{\partial x}=2xe^y+y, \] si calcola \[ \frac{\partial^2 f}{\partial x^2}=2e^y, \quad \frac{\partial^2 f}{\partial y \partial x}=2xe^y+1. \] Ricordando che \[ \frac{\partial f}{\partial y}=x^2e^y-9y^2+x, \] si calcola \[ \frac{\partial^2 f}{\partial x \partial y}=2xe^y+1, \quad \frac{\partial^2 f}{\partial y^2}=x^2e^y-18y. \] Si ottiene quindi la matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}2e^y & 2xe^y+1 \\2xe^y+1 & x^2e^y-18y\end{array}\right). \]
Example 9.8 Riprendendo l’Esempio 9.5, si calcoli la matrice Hessiana della funzione \(f:D_f\subseteq \mathbb{R}^2 \to \mathbb{R}\), definita da \[ f(x,y)=1+2\log (xy) -4 x^2y^2. \] Ricordando che \[ \frac{\partial f}{\partial x}=\frac2x-8xy^2, \] si calcola \[ \frac{\partial^2 f}{\partial x^2}=-\frac{2}{x^2}-8y^2, \quad \frac{\partial^2 f}{\partial y \partial x}=-16xy. \] Ricordando che \[ \frac{\partial f}{\partial y}=\frac2y-8x^2y, \] si calcola \[ \frac{\partial^2 f}{\partial x \partial y}=-16xy, \quad \frac{\partial^2 f}{\partial y^2}=-\frac{2}{y^2}-8x^2. \] Si ottiene quindi la matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}-\frac{2}{x^2}-8y^2 & -16xy \\-16xy & -\frac{2}{y^2}-8x^2\end{array}\right). \]
Negli esempi precedenti le due derivate miste del secondo ordine sono identiche. È infatti possibile dimostrare il seguente teorema, che vale nella totalità dei casi trattati in questo testo.
Theorem 9.1 (Teorema di Schwarz) Se la funzione \(f:A\subseteq \mathbb{R}^2 \to \mathbb{R}\) ammette derivate parziali del secondo ordine continue su \(A\) (e in tal caso \(f\) si dice di classe C2), allora \(f\) possiede derivate miste uguali, ovvero \[ \frac{\partial^2 f}{\partial y \partial x}(x,y)=\frac{\partial^2 f}{\partial x \partial y}(x,y), \quad (x,y) \in A. \]
Il Teorema di Schwarz non deve fornire una scorciatoia per velocizzare il calcolo della matrice Hessiana evitando il calcolo di una delle due derivate miste, ma piuttosto un efficace strumento per verificare se il calcolo delle due derivate miste è stato effettuato correttamente.
9.4 Massimo e minimo di una funzione di due variabili
Esattamente come nel caso univariato, il massimo/minimo assoluto di una funzione di due variabili è definito come il massimo/minimo dei valori assunti dalla funzione, ovvero il massimo/minimo della sua immagine. Analogamente, se ci si restringe a considerare un intorno di un punto, si parlerà di massimo/minimo locale (anche detto relativo).
Se la funzione in oggetto deve essere ottimizzata, ovvero se ne devono cercare eventuali massimo e minimo, essa prenderà il nome di funzione obiettivo.
Definition 9.6 Data una funzione \(f: A \subseteq \mathbb{R}^2 \to \mathbb{R}\):
\((x_M,y_M) \in A\) si dice punto di massimo assoluto per \(f\) se \[ f(x_M,y_M) \geq f(x,y), \text{ per ogni } (x,y) \in A. \] Il valore \(f(x_M,y_M)\) è detto massimo assoluto di \(f\);
\((x_M,y_M) \in A\) si dice punto di massimo locale (o relativo) per \(f\) se \[ f(x_M,y_M) \geq f(x,y), \text{ per ogni } (x,y) \in I(x_M,y_M) \cap A. \] Il valore \(f(x_M,y_M)\) è detto massimo locale (o relativo) di \(f\).
Definition 9.7 Data una funzione \(f: A \subseteq \mathbb{R}^2 \to \mathbb{R}\):
\((x_m,y_m) \in A\) si dice punto di minimo assoluto per \(f\) se \[ f(x_m,y_m) \leq f(x,y), \text{ per ogni } (x,y) \in A. \] Il valore \(f(x_m,y_m)\) è detto minimo assoluto di \(f\);
\((x_m,y_m) \in A\) si dice punto di minimo locale (o relativo) per \(f\) se \[ f(x_m,y_m) \leq f(x,y), \text{ per ogni } (x,y) \in I(x_m,y_m) \cap A. \] Il valore \(f(x_m,y_m)\) è detto minimo locale (o relativo) di \(f\).
Segue immediatamente dalla definizione che un punto di massimo/minimo assoluto è anche locale, ma non viceversa.
In generale se si parla di massimo/minimo di una funzione (senza aggiungere un aggettivo), si intende il massimo/minimo assoluto. Nei grafici delle funzioni di seguito, identificheremo i punti di massimo/minimo locale o assoluto con un circoletto pieno.
L’ottimizzazione di una funzione bivariata procede analogamente a quella di una funzione univariata. Una funzione può avere punti di massimo/minimo:
nei punti interni al suo dominio;
nei punti di frontiera inclusi nel suo dominio.
Nella sezione di seguito, cominceremo ad analizzare il caso in cui il dominio della funzione sia aperto, ovvero tutti i punti del suo dominio risultino essere interni.
9.5 Ottimizzazione su un insieme aperto (A)
Assumiamo che un punto \((x_0,y_0)\) interno al dominio sia di massimo o di minimo relativo per la funzione di due variabili \(f(x,y)\), che supponiamo ammettere derivate del primo ordine. Allora, lo sarà anche per la funzione di una variabile \(f(x,y_0)\) dove si è fissato il valore \(y=y_0\). Sappiamo quindi dal Capitolo 5 che la derivata di tale funzione, che altro non è che la derivata parziale di \(f(x,y)\) rispetto alla prima variabile \(x\), dovrà annullarsi nel punto \(x=x_0\). Analogamente, si dovrà avere l’annullamento della derivata parziale di \(f(x,y)\) rispetto alla seconda variabile \(y\), nel punto \(y=y_0\). Ne segue che un punto di massimo/minimo locale interno al dominio di una funzione dovrà necessariamente avere derivate parziali nulle, ovvero essere un punto stazionario.
Theorem 9.2 (Condizione del primo ordine per punti di massimo/minimo) Data la funzione \(f:A \subseteq \mathbb{R}^2 \to \mathbb{R}\), sia \((x_M,y_M) \in A\) un suo punto di massimo locale (o di minimo locale) interno al suo dominio. Se \(f\) ammette derivate del primo ordine in \((x_M,y_M)\), allora \[ \frac{\partial f}{\partial x}(x_M,y_M) =0, \quad \frac{\partial f}{\partial y}(x_M,y_M) =0. \]
La condizione del primo ordine non è sufficiente a garantire che un punto stazionario sia in effetti un punto di massimo/minimo, locale o assoluto, ma è solamente un requisito necessario. Analizziamo due diversi esempi in cui la condizione è soddisfatta.
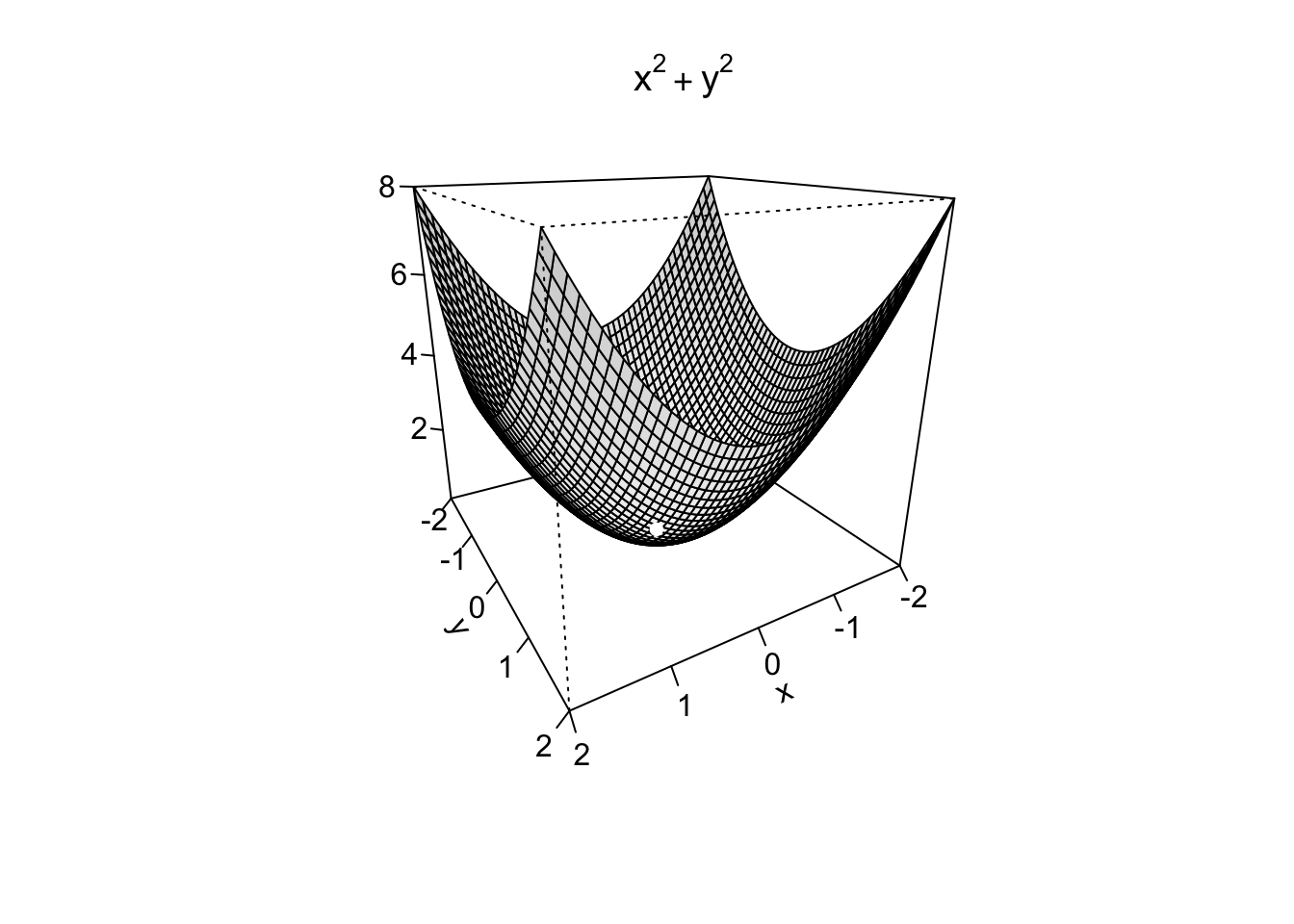
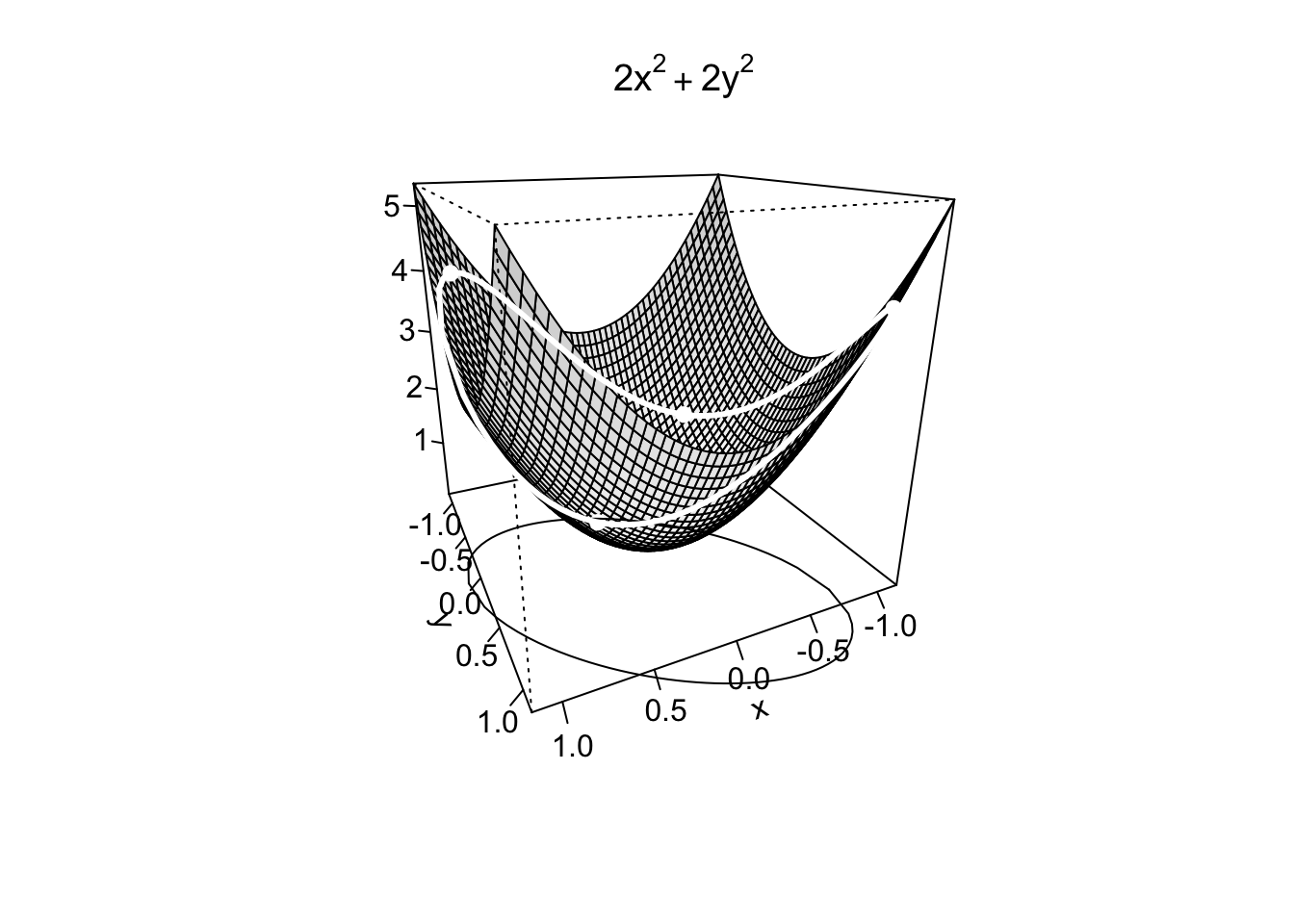
Example 9.9 Si consideri la funzione \(f:\mathbb{R}^2 \to \mathbb{R}, f(x,y)=x^2+y^2\). Calcolando le sue derivate parziali e uguagliandole a zero, si ottiene il sistema \[ \begin{cases} \frac{\partial f}{\partial x}=2x=0, \\ \frac{\partial f}{\partial y}=2y=0, \end{cases} \] da cui si trova l’unico punto stazionario \((x_m,y_m)=(0,0)\). Dato che \[ f(x,y)=x^2+y^2 \geq 0=f(0,0), \text{ per ogni } (x,y) \in \mathbb{R}^2, \] è immediato verificare che esso è un punto di minimo assoluto per \(f\); si veda la figura seguente.
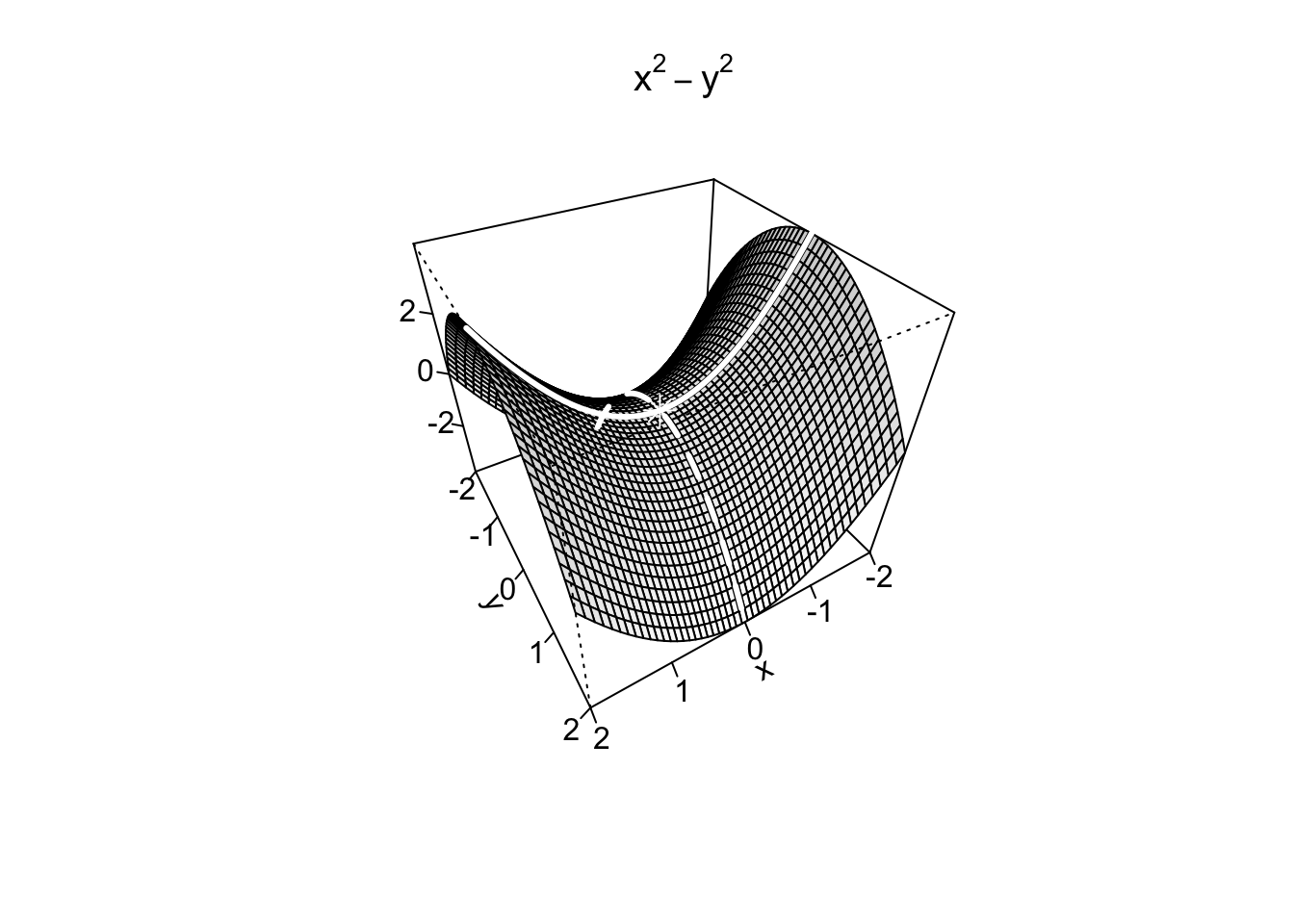
Example 9.10 Si consideri adesso la funzione \(f:\mathbb{R}^2 \to \mathbb{R}, f(x,y)=x^2-y^2\). Calcolando le sue derivate parziali e uguagliandole a zero, si ottiene il sistema \[ \begin{cases} \frac{\partial f}{\partial x}=\phantom{-}2x=0, \\ \frac{\partial f}{\partial y}=-2y=0, \end{cases} \] da cui si trova, come nell’esempio precedente, l’unico punto stazionario \((x_s,y_s)=(0,0)\). Dalla figura seguente si deduce però che questo non è né un punto di massimo, né un punto di minimo.
Si osservi infatti che la funzione \(f(x,0)=x^2\), ottenuta fissando il valore della seconda variabile \(y=0\), ha un punto di minimo assoluto in \(x=0\); la funzione \(f(0,y)=-y^2\), ottenuta fissando il valore della prima variabile \(x=0\), ha invece un punto di massimo assoluto in \(y=0\). Conseguentemente, in qualsiasi intorno del punto stazionario trovato, la funzione assume sia valori positivi che valori negativi, ovvero sia più grandi che più piccoli del valore assunto in \((0,0)\). Un punto con queste caratteristiche è detto punto di sella (l’immagine seguente richiama appunto la forma di una sella).
Definition 9.8 Data una funzione \(f: A \subseteq \mathbb{R}^2 \to \mathbb{R}\), un suo punto interno stazionario \((x_s,y_s) \in A\) si dice punto di sella per \(f\) se per qualsiasi \(r>0\) è possibile trovare due punti \((x_r,y_r),(x'_r,y'_r) \in I_r(x_s,y_s)\cap A\) tali che \[ f(x_r,y_r) < f(x_s,y_s) < f(x'_r,y'_r), \] ovvero se il punto stazionario non è né un punto di minimo locale né un punto di massimo locale.
Nei grafici delle funzioni di seguito, identificheremo i punti di sella con un asterisco.
Per poter stabilire la natura di un punto stazionario, come nel caso univariato, è quindi necessario reperire una informazione migliore di quella fornita dalle derivate del primo ordine. Nel caso bidimensionale, non è nemmeno sufficiente studiare il segno delle derivate parziali, come si vede dall’esempio appena svolto. Condizioni sufficienti per garantire l’esistenza di un massimo/minimo interno si devono necessariamente basare sulle derivate del secondo ordine.
Per enunciare le condizioni del secondo ordine, ricordiamo la definizione di determinante di una matrice \(2\times2\) data nel Capitolo 8.
Definition 9.9 Si dice determinante della matrice Hessiana \(H_f(x,y)\) definita in (9.1)
il prodotto degli elementi della diagonale meno il prodotto degli altri elementi (della diagonale secondaria):
\[
\text{det}(H_f(x,y)) = \frac{\partial^2 f}{\partial x^2}\frac{\partial^2 f}{\partial y^2}-\frac{\partial^2 f}{\partial x \partial y}\frac{\partial^2 f}{\partial y \partial x}.
\]
Inoltre, è necessario assumere che il dominio \(A\) della funzione da ottimizzare sia convesso, ovvero che, per ogni coppia di punti \((x_1,y_1),(x_2,y_2) \in A\), anche tutti i punti del segmento che li unisce appartengano ad \(A\).
Theorem 9.3 (Condizioni del secondo ordine per punti di massimo/minimo ASSOLUTI) Sia \(f: A \subseteq \mathbb{R}^2 \to \mathbb{R}\), con \(A\) insieme aperto e convesso, una funzione di classe C2 con matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}\frac{\partial^2 f}{\partial x^2}(x,y) & \frac{\partial^2 f}{\partial y \partial x}(x,y) \\ \frac{\partial^2 f}{\partial x \partial y}(x,y)& \frac{\partial^2 f}{\partial y^2}(x,y)\end{array}\right), \] e sia \((x,y) \in A\) un suo punto (interno) stazionario.
Se, per ogni \((x,y)\in A\), si ha che \(\text{det}(H_f(x,y)) \geq 0\), ed inoltre:
- \(\frac{\partial^2 f}{\partial x^2}(x,y)\leq 0\), allora \((x,y)\) è un punto di massimo assoluto;
- \(\frac{\partial^2 f}{\partial x^2}(x,y)\geq 0\), allora \((x,y)\) è un punto di minimo assoluto.
Remark. Osserviamo i seguenti punti fondamentali sul Teorema 9.3:
le due condizioni corrispondono al caso in cui la funzione sia concava (\(\frac{\partial^2 f}{\partial x^2}(x,y)\leq 0\)) o convessa (\(\frac{\partial^2 f}{\partial x^2}(x,y)\geq 0\)) sul suo dominio. La definizione di convessità per funzioni di due variabili è analoga a quella data nel Capitolo 1 (considerando punti di \(\mathbb{R}^2\) come vettori riga o colonna, si veda il Capitolo 8), richiedendo che il dominio della funzione sia convesso. Si osservi l’analogia con la condizione del secondo ordine nel caso unidimensionale (Teorema 5.4), dove una derivata seconda negativa (positiva) identificava un punto di massimo (minimo);
le condizioni del teorema sono sufficienti ad identificare un punto di massimo/minimo assoluto ma sono anche molto forti: devono valere sull’intero dominio (aperto e convesso) della funzione;
il teorema nulla predice nel caso in cui non valgano le condizioni citate, né le sue condizioni sono necessarie: è possibile trovare funzioni aventi un punto di massimo/minimo assoluto che non le soddisfano;
entrambe le condizioni sono soddisfatte ad esempio dalla funzione costante (sia concava che convessa) in cui ogni punto è stazionario (le derivate del primo ordine sono nulle) ed è sia di massimo che di minimo (tutte le derivate del secondo ordine sono nulle).
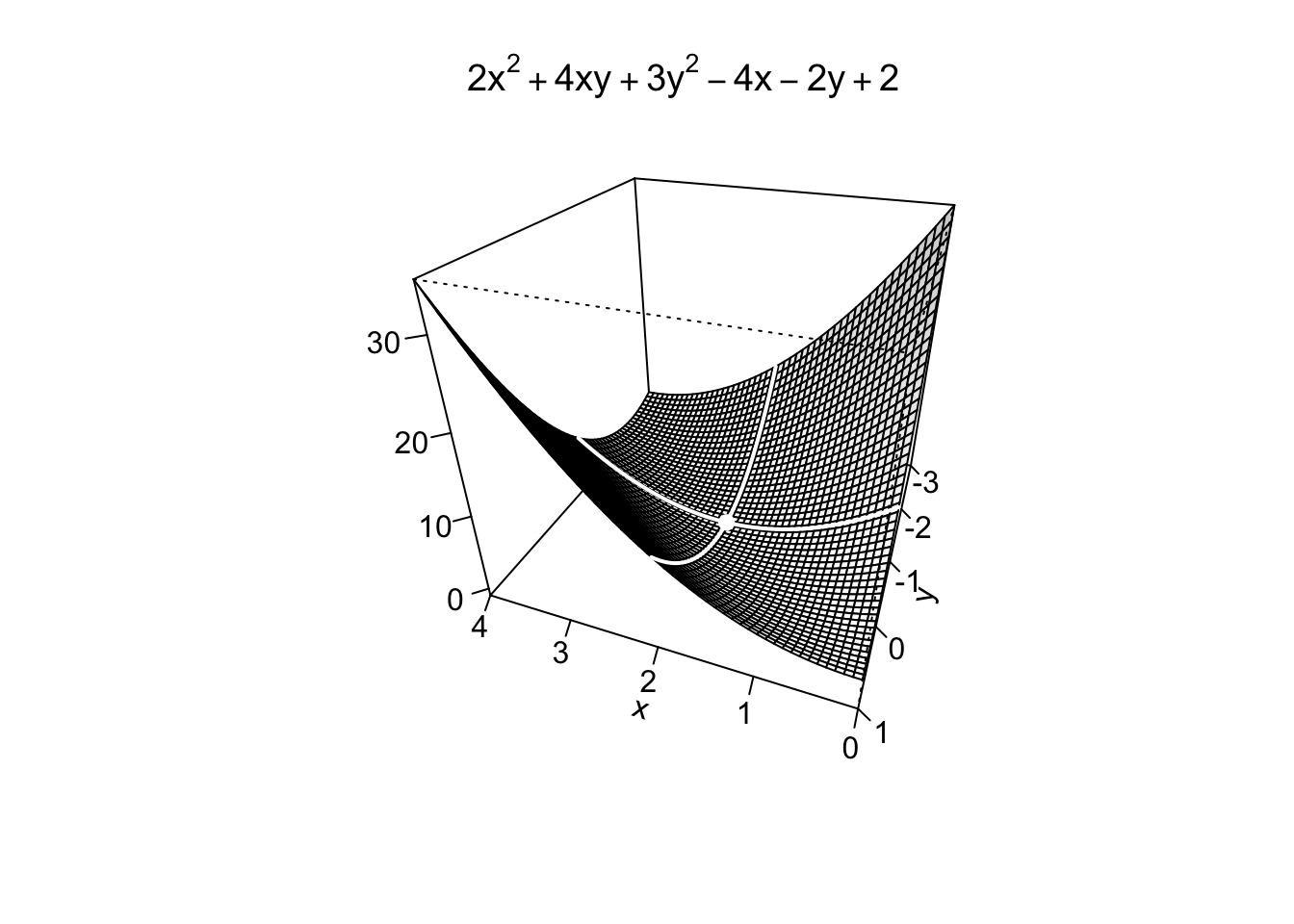
Example 9.11 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) definita da \[ f(x,y)=2x^2+4xy+3y^2-4x-2y+2. \] Essendo il dominio della funzione un insieme aperto, quindi avente tutti i suoi punti interni, un massimo/minimo assoluto (che è anche relativo) deve forzatamente essere collocato su un punto stazionario.
Si cercano quindi eventuali punti stazionari della funzione calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema: \[ \begin{cases} \frac{\partial f}{\partial x}=4x+4y-4=0, \\ \frac{\partial f}{\partial y}=4x+6y-2=0. \end{cases} \quad \Rightarrow \quad \begin{cases} x+y-1&=0, \\ 2x+3y-1&=0. \end{cases} \] Sostituendo \(x=1-y\) nella seconda equazione, si ottiene \[ 2(1-y)+3y-1=2-2y+3y-1=y+1=0 \quad \Rightarrow \quad y=-1. \] Dalla prima equazione del sistema si trova \(x=1-y=1+1=2\). La funzione possiede quindi l’unico punto stazionario \((2,-1)\). Per capirne la natura, si calcola la matrice Hessiana. Essendo la funzione \(f(x,y)\) un polinomio di secondo grado, derivando due volte si ottiene una matrice Hessiana costante: \[ H_f(x,y)=\left(\begin{array}{cc}4 & 4 \\ 4 & 6\end{array}\right). \]
Controllando quindi le condizioni del Teorema 9.3, per ogni \((x,y)\in \mathbb{R}^2\) si ha che
\[
\text{det}(H_f(x,y)) = 4 \cdot 6-4 \cdot 4=24-16=8 >0 \quad \text{ e } \quad \frac{\partial^2 f}{\partial x^2}(x,y)=4> 0.
\]
Risulta quindi che il punto \((2,-1)\) è un punto di minimo assoluto.
Si osservi che la funzione non può avere un punto di massimo, altrimenti lo avremmo trovato tra i punti stazionari.
La funzione (ovvero la sua immagine) è infatti illimitata superiormente, come si può verificare ad esempio fissando il valore di \(y=0\)
e calcolando
\[
\lim_{x \to +\infty} f(x,0)=2x^2-4x+2=+\infty.
\]
La funzione quindi assume valori arbitrariamente grandi e non ha quindi (punto di) massimo.
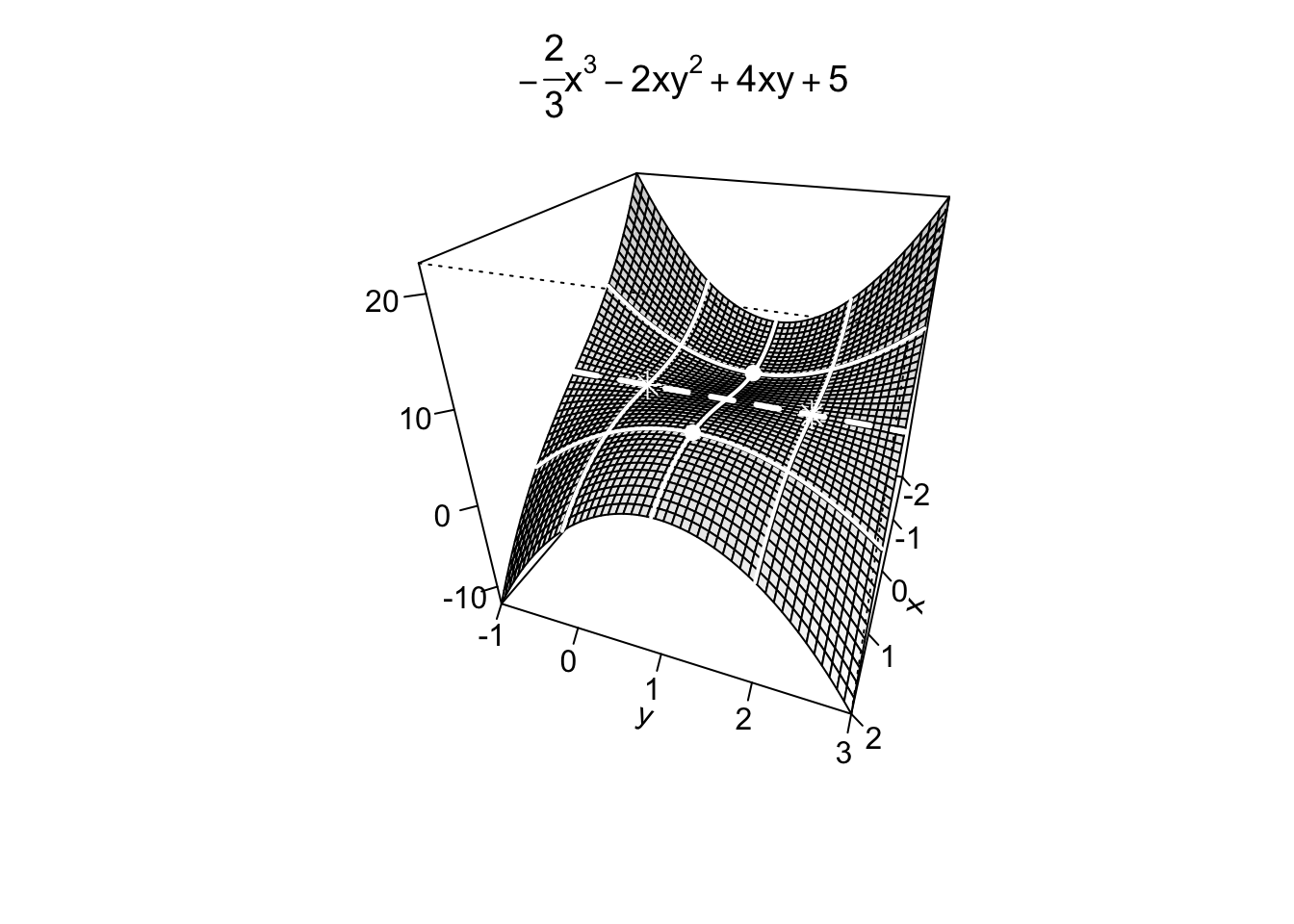
Example 9.12 Si trovino e si classifichino tutti i punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) definita da \[ f(x,y)=-\frac23x^3 -2xy^2 +4xy +5, \] indicando se essi sono punti di massimo/minimo assoluto o relativo, oppure punti di sella.
Si cercano i punti stazionari della funzione calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema: \[ \begin{cases} \frac{\partial f}{\partial x}=-2x^2-2y^2+4y=0, \\ \frac{\partial f}{\partial y}=-4xy+4x=0. \end{cases} \quad \Rightarrow \quad \begin{cases} -x^2-y^2+2y&=0, \\ -4x(y-1)&=0. \end{cases} \]
Il sistema rappresentante la condizione di annullamento delle due derivate parziali non è in generale lineare, nè si presta ad un metodo di risoluzione generale. Quando è possibile, si può operare per sostituzione o, come in questo caso, discutere i casi implicati dalla legge di annullamento del prodotto, se una delle due equazioni è una moltiplicazione tra due fattori.
Per trovare tutti i punti stazionari, si discutono i seguenti casi:
se \(x \neq 0\), dalla seconda equazione (per la legge di annullamento del prodotto) si ha che \(y=1\). Sostituendo nella prima, si ricava: \[ -x^2-1+2=0 \quad \Rightarrow \quad x^2=1, \] ovvero \(x=\pm 1\). Si trovano quindi i due punti stazionari \((1,1)\) e \((-1,1)\);
se \(y \neq 1\), dalla seconda equazione si ha che \(x=0\). Sostituendo nella prima, si ricava: \[ -y^2+2y=0 \quad \Rightarrow \quad y(-y+2)=0, \] che ha come soluzioni \(y=0,2\). Si trovano quindi i due punti stazionari \((0,0)\) e \((0,2)\);
nel caso rimanente, ovvero se \(x=0\) e \(y=1\), la prima equazione non è soddisfatta.
Risultano quindi i quattro punti stazionari: \[(1,1),\quad (-1,1),\quad (0,0),\quad (0,2).\] Per capirne la natura, si calcola la matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}-4x & -4y+4 \\ -4y+4 & -4x\end{array}\right)=4\left(\begin{array}{cc}-x & -y+1 \\ -y+1 & -x\end{array}\right). \] In questo esempio, si osservi che \(\text{det}(H_f(x))=(-4x)^2-(-4y+4)^2\) non mantiene lo stesso segno su tutto \(\mathbb{R}^2\), quindi il Teorema 9.3 non è applicabile.
In casi come quelli descritti nell’esempio precedente, le forti ipotesi del Teorema 9.3 non sono soddisfatte. Serve quindi un risultato che abbia una maggiore applicazione.
Theorem 9.4 (Condizioni del secondo ordine per punti di massimo/minimo LOCALI) Sia \(f: A \subseteq \mathbb{R}^2 \to \mathbb{R}\), con \(A\) insieme aperto, una funzione di classe C2. Sia \((x,y) \in A\) un suo punto interno stazionario in cui si calcola la matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}\frac{\partial^2 f}{\partial x^2}(x,y) & \frac{\partial^2 f}{\partial y \partial x}(x,y) \\ \frac{\partial^2 f}{\partial x \partial y}(x,y)& \frac{\partial^2 f}{\partial y^2}(x,y)\end{array}\right). \]
Se \(\text{det}(H_f(x,y)) < 0\), allora \((x,y)\) è un punto di sella;
se \(\text{det}(H_f(x,y)) > 0\), ed inoltre:
\(\frac{\partial^2 f}{\partial x^2}(x,y)< 0\), allora \((x,y)\) è un punto di massimo locale;
\(\frac{\partial^2 f}{\partial x^2}(x,y)> 0\), allora \((x,y)\) è un punto di minimo locale.
Remark. Osserviamo i seguenti punti fondamentali sul Teorema 9.4:
le due condizioni corrispondono al caso in cui la funzione sia strettamente concava (\(\frac{\partial^2 f}{\partial x^2}(x,y)< 0\)) o strettamente convessa (\(\frac{\partial^2 f}{\partial x^2}(x,y)> 0\)) nell’intorno del punto stazionario. Si osservi l’analogia con le condizioni del secondo ordine nel caso unidimensionale (Teorema 5.4), dove una derivata seconda negativa (positiva) identificava un punto di massimo (minimo);
le condizioni del Teorema 9.4 sono applicabili in un numero di casi maggiore rispetto al Teorema 9.3, ma le sue conclusioni sono forzatamente più deboli e hanno valore locale (relativo) ma non assoluto (globale). È semplice capirne il motivo: la matrice Hessiana calcolata in un punto non potrà mai fornire informazioni su tutto il dominio della funzione, ma solo relativamente ad un intorno di quel punto. L’informazione data da questo teorema ha quindi carattere locale, e non globale;
il teorema nulla predice nel caso in cui non valgano le condizioni citate, come ad esempio nel caso in cui \(\text{det}(H_f(x,y)) = 0\).
Possiamo utilizzare il Teorema 9.4 per completare l’Esempio 9.12.
Example 9.13 Si trovino e si classifichino tutti i punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) definita da \[ f(x,y)=-\frac23x^3 -2xy^2 +4xy +5, \] indicando se essi sono punti di massimo/minimo assoluto o relativo oppure punti di sella.
Nell’Esempio 9.12 si erano trovati i quattro punti stazionari \((1,1)\), \((-1,1)\), \((0,0)\), e \((0,2)\), e la matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}-4x & -4y+4 \\ -4y+4 & -4x\end{array}\right)=4\left(\begin{array}{cc}-x & -y+1 \\ -y+1 & -x\end{array}\right). \] Calcolando la matrice Hessiana nei quattro punti stazionari, si possono riassumere le conclusioni derivanti dal Teorema 9.4 nella seguente tabella:Come già osservato, le conclusioni del Teorema 9.4 non possono avere carattere globale. Resta dunque da determinare se i punti di massimo/minimo relativo trovati siano anche assoluti.
Per farlo, si può ad esempio verificare se la funzione è illimitata. Dato che compare il termine \(-\frac23 x^3\), è immediato verificare, fissando \(y=0\), che \[\begin{align*} \lim_{x \to +\infty} f(x,0)&=\lim_{x \to +\infty} -\frac23 x^3+5 =-\infty, \\ \lim_{x \to -\infty} f(x,0)&=\lim_{x \to -\infty} -\frac23 x^3+5 =+\infty, \end{align*}\] quindi la funzione risulta assumere valori sia arbitrariamente grandi che arbitrariamente piccoli. I punti di massimo/minimo relativo trovati quindi non sono punti di massimo/minimo assoluto.
Se, fissando opportunamente una delle due variabili, la funzione risulta essere illimitata superiormente (inferiormente), si ha la certezza dell’inesistenza di un massimo (minimo) assoluto. Viceversa, se questo non risultasse vero o non si scegliesse idoneamente il valore della variabile da fissare, il problema della determinazione della natura del punto stazionario in oggetto rimarrebbe aperto, rendendo necessario un ulteriore approfondimento. In generale, l’ottimizzazione in più dimensioni è un problema difficile, anche numericamente, e non è al momento noto un algoritmo di risoluzione generale.
Attenzione al testo dell’esercizio! Se nell’Esempio 9.13 fosse stato chiesto di ottimizzare la funzione (trovare il suo massimo/minimo assoluto), sarebbe stato sufficiente calcolare gli ultimi due limiti per dimostrare che le funzione non ammette nè massimo nè minimo assoluto.
Schema di risoluzione completo di una ottimizzazione su un insieme aperto (A):
si controlla che il dominio sia aperto: tutti i suoi punti sono interni (caso A);
eventuali massimi/minimi relativi/assoluti possono essere raggiunti solo su punti stazionari, che quindi si ricercano uguagliando a zero le due derivate parziali;
si calcola la matrice Hessiana per determinare la natura dei punti stazionari trovati;
si stabilisce se si può utilizzare il Teorema 9.3 per ottenere delle conclusioni globali, oppure il Teorema 9.4 per ottenere delle conclusioni locali;
si cerca di stabilire se eventuali punti di massimo/minimo relativo siano anche assoluti (questo punto si può affrontare immediatamente a seconda della richiesta del problema da risolvere).
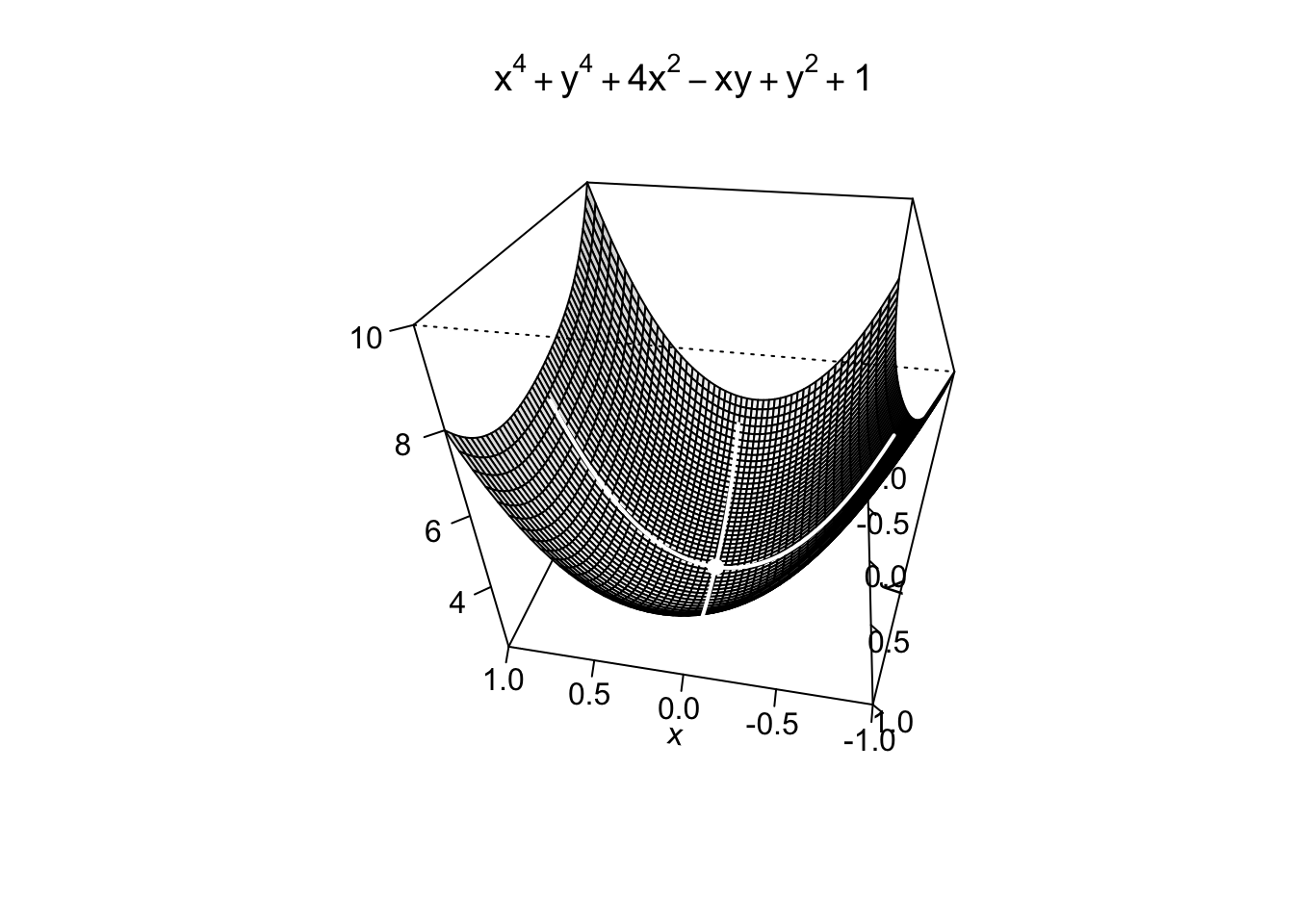
Example 9.14 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) definita da \[ f(x,y)=x^4+y^4+4x^2-xy+y^2+1. \] Essendo il dominio della funzione un insieme aperto, quindi avente tutti i suoi punti interni, un massimo/minimo assoluto (che è anche relativo) deve forzatamente essere raggiunto su un punto stazionario.
Si cercano quindi eventuali punti stazionari della funzione calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema: \[ \begin{cases} \frac{\partial f}{\partial x}=4x^3+8x-y=0, \\ \frac{\partial f}{\partial y}=4y^3-x+2y=0. \end{cases} \] La soluzione di questo sistema non sembra agevole. Si osservi comunque che, essendo i termini noti entrambi nulli, esso possiede almeno la soluzione nulla \(x=0\), \(y=0\). Si ha quindi che \((0,0)\) è un punto stazionario.
Per capirne la natura, si calcola la matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}12x^2+8 & -1 \\ -1 & 12y^2+2\end{array}\right). \] Controllando quindi le condizioni del Teorema 9.3, per ogni \((x,y)\in \mathbb{R}^2\), si ha che \[\begin{align*} \text{det}(H_f(x,y)) =(12x^2+8)(12y^2+2)-1 \geq 15 &>0,\\ \frac{\partial^2 f}{\partial x^2}(x,y)=12x^2+8 \geq 8&> 0. \end{align*}\] Risulta quindi che il punto \((0,0)\) è un punto di minimo assoluto per \(f\).
Ai fini dell’applicazione del Teorema 9.3 è rilevante che il segno di \(\text{det}(H_f(x,y))\) permanga positivo su tutto il dominio, non che la matrice Hessiana sia costante (non dipenda dal punto \((x,y)\)).
Si osservi che la funzione non può avere un punto di massimo, perché è illimitata superiormente, come si può ad esempio verificare fissando il valore \(x=0\) e calcolando \[ \lim_{y \to +\infty} f(0,y)=y^4+y^2+1=+\infty. \]
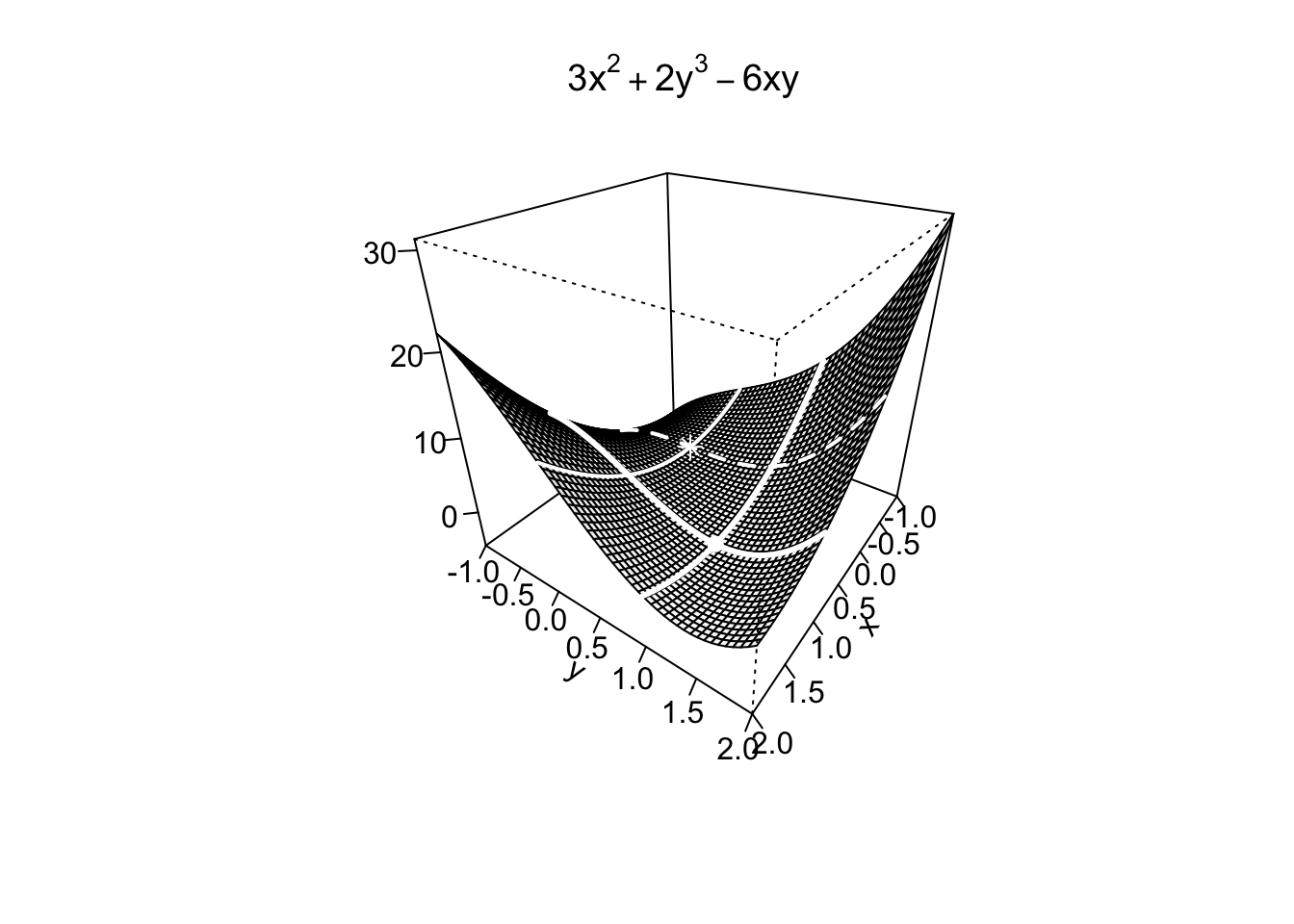
Example 9.15 Si trovino e si classifichino tutti i punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) definita da \[ f(x,y)=3x^2+2y^3-6xy, \] indicando se essi sono punti di massimo/minimo assoluto o relativo oppure punti di sella.
Si cercano i punti stazionari della funzione calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema: \[ \begin{cases} \frac{\partial f}{\partial x}=6x-6y=0, \\ \frac{\partial f}{\partial y}=6y^2-6x=0. \end{cases} \quad \Rightarrow \quad \begin{cases} x-y&=0, \\ 6(y^2-x)&=0. \end{cases} \] Dalla prima equazione si trova \(x=y\). Sostituendo nella seconda si ottiene quindi \[ 6(x^2-x)=6x(x-1)=0, \] da cui si ricava \(x=0,1\). Ricordando (dalla prima equazione) che \(y=x\), si trovano quindi i due punti stazionari \((0,0)\) e \((1,1)\).
Per determinarne la natura, si calcola la matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}6 & -6 \\ -6 & 12y\end{array}\right). \] Si osserva immediatamente che il segno del determinante della matrice Hessiana non permane su tutto \(\mathbb{R}^2\), quindi si deve utilizzare il Teorema 9.4, le cui conclusioni sono riassunte nella seguente tabella:La funzione non ammette (punto di) massimo assoluto, altrimenti lo avremmo trovato tra i punti stazionari. Resta dunque da determinare se il punto di minimo relativo trovato sia anche assoluto o meno.
Per farlo, si verifica, fissando \(x=0\), che \[ \lim_{y \to -\infty} f(0,y)=\lim_{y \to -\infty} 2y^3 =-\infty, \] quindi la funzione risulta assumere valori arbitrariamente piccoli e non possiede minimo assoluto.
9.6 Ottimizzazione vincolata con vincoli sostituibili (B)
Molto spesso le funzioni sono ottimizzate tenendo conto di condizioni (vincoli) che ne restringono il dominio sul quale cercare i punti di massimo/minimo. Il nuovo dominio, differente quindi dal dominio (naturale) della funzione, è detto dominio di ottimizzazione.
Iniziamo con lo studiare problemi di ottimizzazione vincolata considerando i casi più semplici in cui il dominio è ristretto da uno o più vincoli che si possono direttamente sostituire all’interno della funzione da ottimizzare, trasformando così l’ottimizzazione da bivariata ad univariata.
Example 9.16 Tra tutti i rettangoli di semi-perimetro fissato, si determinino quelli aventi area massima e minima.
Questo è un problema classico che illustra come operare con vincoli che si possono sostituire direttamente all’interno della funzione da ottimizzare (caso B).
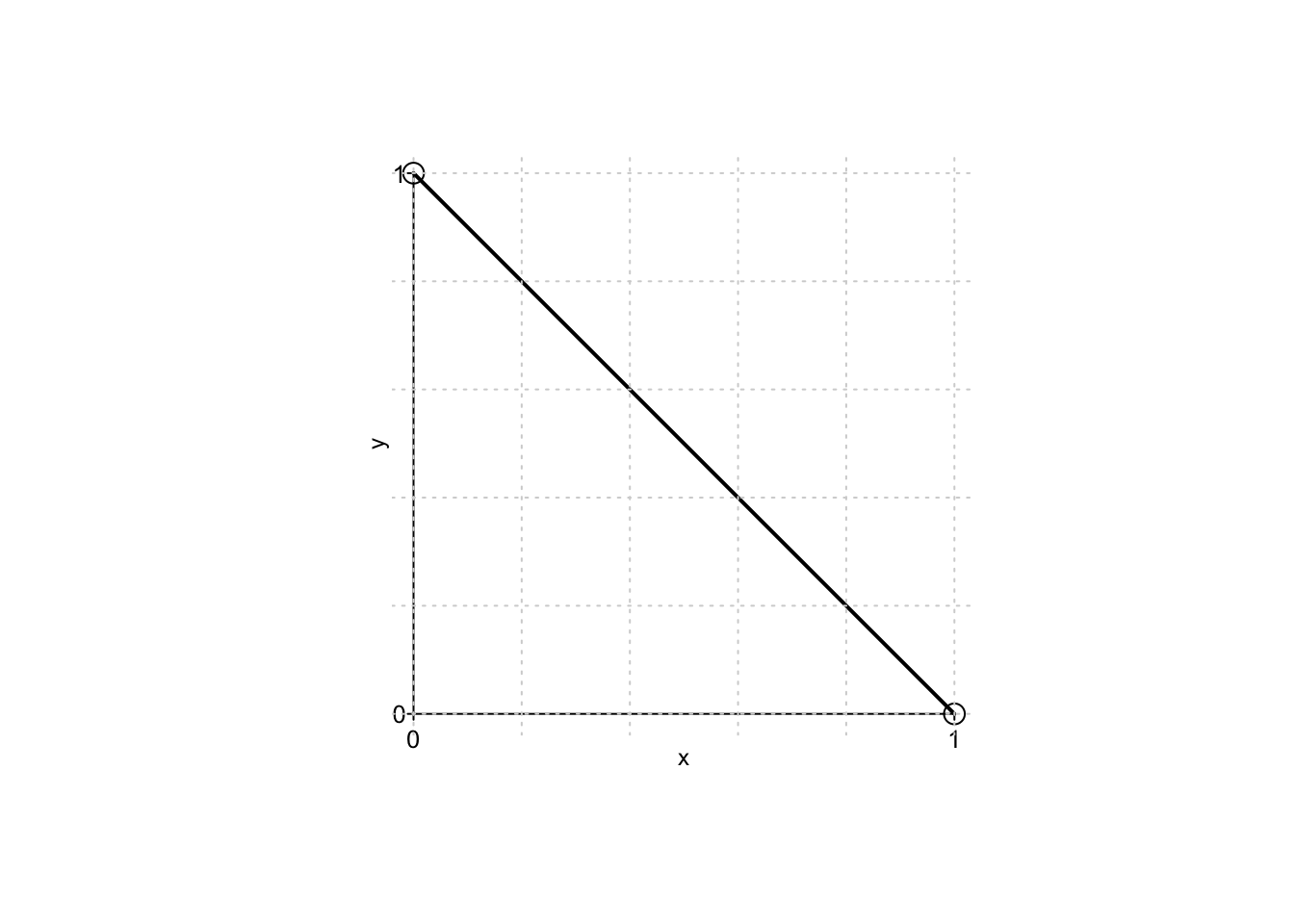
Detti \(x >0\) ed \(y>0\) i due lati di un arbitrario rettangolo, e fissando il suo semi-perimetro pari ad 1 (\(x+y=1\)), si cercano i punti di massimo/minimo della funzione \(f:A\subseteq \mathbb{R}^2 \to \mathbb{R}\), \[ f(x,y)=xy, \quad \text{ sull'insieme } \quad A=\{(x,y)\in \mathbb{R}^2: x+y=1, x>0,y>0\}. \] Per semplicità, scriveremo più brevemente il problema come \[ \max,\min f(x,y)=xy, \quad \text{ sull'insieme } \quad A=\{x+y=1,x>0,y>0\}. \] Se possibile, è utile raffigurare il dominio di ottimizzazione della funzione, ovvero l’insieme su cui andranno cercati punti di massimo e minimo. In questo caso, la retta \(y=1-x\) viene ridotta ad un segmento dalle condizioni di positività delle variabili.
 A questo punto basta sostituire una delle due variabili, ad esempio \(y=1-x\), all’interno della funzione
da ottimizzare, andando poi a cercare massimo e minimo di una funzione di una sola variabile.
Nel farlo, è fondamentale capire il dominio di ottimizzazione della variabile restante. In questo caso,
si vede in figura che la variabile \(x\) varia nell’intervallo \((0,1)\). Si ha quindi il nuovo problema
\[
\max,\min f(x,1-x)=x(1-x)=x-x^2, \quad \text{ sull'insieme } \quad A_x=(0,1).
\]
Quella sotto studio è adesso una parabola concava che possiede un punto di massimo assoluto nel suo vertice (se compreso nel dominio di ottimizzazione \(A_x\)), e non ha punti di minimo dato che l’intervallo \(A_x\) è un insieme aperto. Dato che il vertice della parabola è situato nel punto \(x=\frac12\), si ha dunque che la funzione originaria da ottimizzare ha un punto di massimo assoluto in \(x=\frac12\) e \(y=1-x=\frac12\), e non ha punti di minimo.
A questo punto basta sostituire una delle due variabili, ad esempio \(y=1-x\), all’interno della funzione
da ottimizzare, andando poi a cercare massimo e minimo di una funzione di una sola variabile.
Nel farlo, è fondamentale capire il dominio di ottimizzazione della variabile restante. In questo caso,
si vede in figura che la variabile \(x\) varia nell’intervallo \((0,1)\). Si ha quindi il nuovo problema
\[
\max,\min f(x,1-x)=x(1-x)=x-x^2, \quad \text{ sull'insieme } \quad A_x=(0,1).
\]
Quella sotto studio è adesso una parabola concava che possiede un punto di massimo assoluto nel suo vertice (se compreso nel dominio di ottimizzazione \(A_x\)), e non ha punti di minimo dato che l’intervallo \(A_x\) è un insieme aperto. Dato che il vertice della parabola è situato nel punto \(x=\frac12\), si ha dunque che la funzione originaria da ottimizzare ha un punto di massimo assoluto in \(x=\frac12\) e \(y=1-x=\frac12\), e non ha punti di minimo.
In conclusione, tra tutti i rettangoli di (semi-)perimetro fissato, quello avente area massima è il quadrato (\(x=y=\frac12\)), mentre non ha senso chiedersi quale sia quello con area minima (facendo tendere la lunghezza di uno dei due lati a \(0\), si potrà diminuire l’area a piacimento).
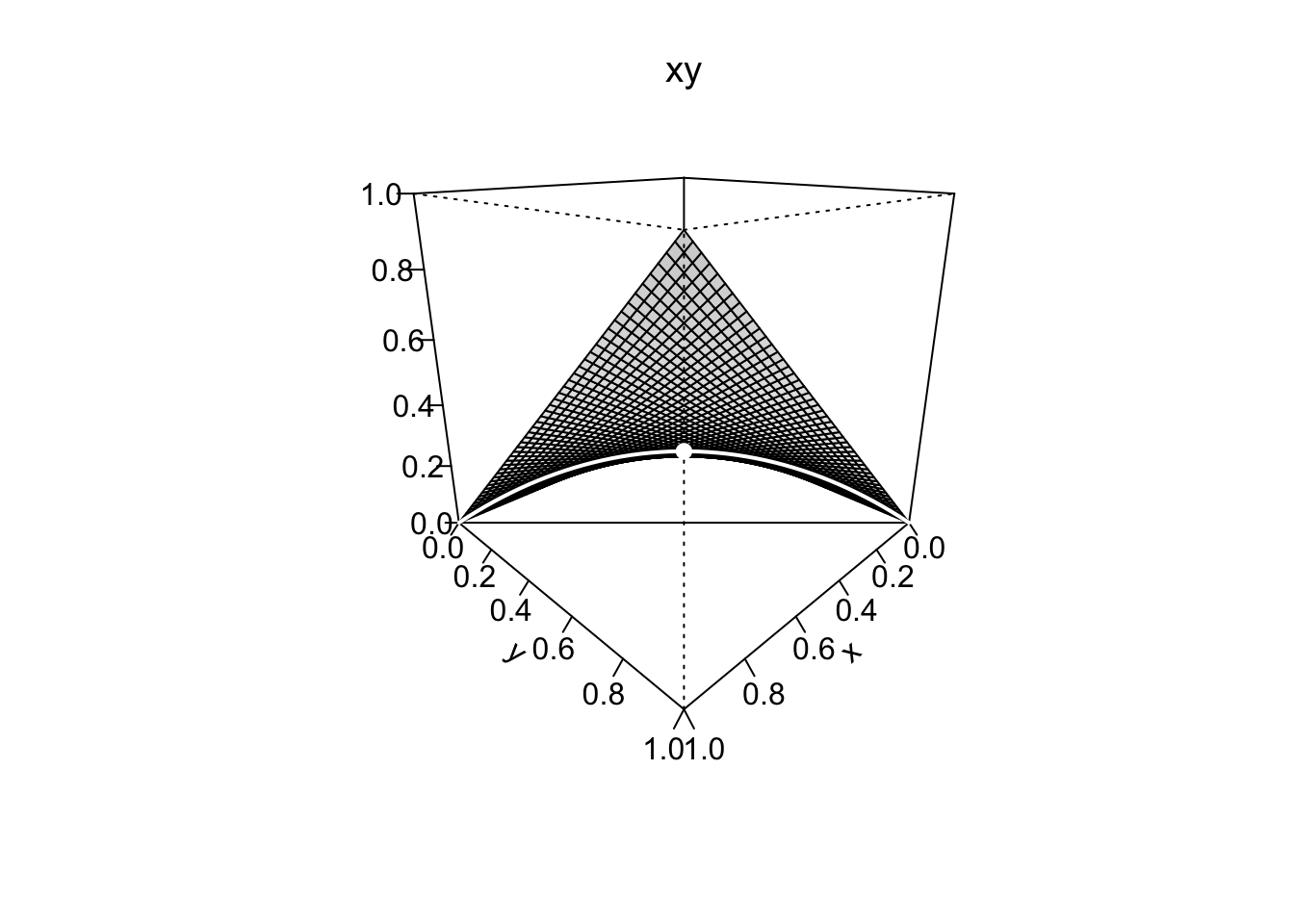
La soluzione nell’Esempio 9.16 corrisponde (con vincoli di non negatività delle variabili) a quella del problema economico di un consumatore con funzione di utilità \(u(x,y)=xy\) che deve scegliere quante unità \(x\geq 0\) di un primo bene avente prezzo unitario \(p_x\), e \(y \geq 0\) di un secondo bene avente prezzo unitario \(p_y\) acquistare sotto il vincolo di bilancio \[ \{p_x\,x+p_y\,y = k, x \geq 0, y \geq 0\}. \] Si veda a questo proposito l’Esempio 9.21.
Example 9.17 Tra tutti i rettangoli di area fissata, si determinino quelli aventi semi-perimetro massimo e minimo.
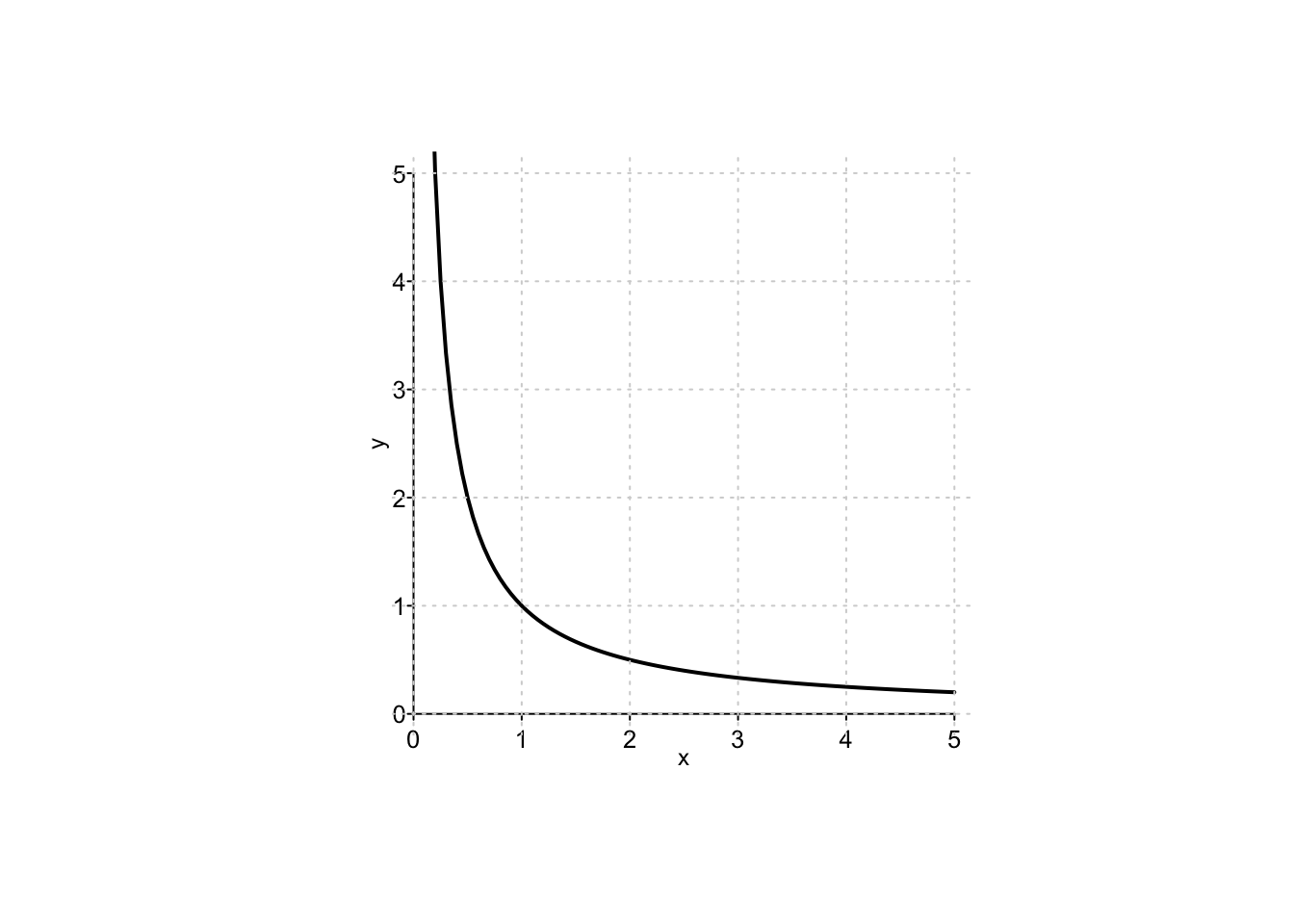
Detti \(x >0\) ed \(y>0\) i due lati di un arbitrario rettangolo, e fissando la sua area pari ad 1, si cerca dunque la soluzione del problema \[ \max,\min f(x,y)=x+y \quad \text{ sull'insieme } \quad A=\{xy=1, x>0,y>0\}. \] Il dominio di ottimizzazione della funzione è in questo caso l’iperbole \(y=\frac1x\) considerata nel primo quadrante del piano cartesiano:
 A questo punto basta sostituire una delle due variabili, ad esempio \(y=\frac1x\) all’interno della funzione
da ottimizzare, andando poi a cercare massimo e minimo di una funzione di una sola variabile.
La variabile rimanente \(x\) varia nell’intervallo \((0,+\infty)\). Si ha quindi il nuovo problema
\[
\max,\min f\left(x,\frac1x\right)=x+\frac1x, \quad \text{ sull'insieme } \quad A_x=(0,+\infty).
\]
Dato che il dominio di ottimizzazione \(A_x\) è un insieme aperto, eventuali punti di massimo/minimo
devono essere localizzati su punti stazionari. Prendendo in considerazione la funzione \(g(x)=x +\frac1x\),
e risolvendo
\[
g'(x)=1-\frac{1}{x^2}=0
\]
si trova l’unico punto stazionario \(x=1\). Calcolando la derivata seconda
\[
g''(x)=\frac{2}{x^3}>0, \quad x >0,
\]
che è sempre positiva nel dominio considerato, si può affermare che il punto stazionario trovato è di minimo assoluto.
A questo punto basta sostituire una delle due variabili, ad esempio \(y=\frac1x\) all’interno della funzione
da ottimizzare, andando poi a cercare massimo e minimo di una funzione di una sola variabile.
La variabile rimanente \(x\) varia nell’intervallo \((0,+\infty)\). Si ha quindi il nuovo problema
\[
\max,\min f\left(x,\frac1x\right)=x+\frac1x, \quad \text{ sull'insieme } \quad A_x=(0,+\infty).
\]
Dato che il dominio di ottimizzazione \(A_x\) è un insieme aperto, eventuali punti di massimo/minimo
devono essere localizzati su punti stazionari. Prendendo in considerazione la funzione \(g(x)=x +\frac1x\),
e risolvendo
\[
g'(x)=1-\frac{1}{x^2}=0
\]
si trova l’unico punto stazionario \(x=1\). Calcolando la derivata seconda
\[
g''(x)=\frac{2}{x^3}>0, \quad x >0,
\]
che è sempre positiva nel dominio considerato, si può affermare che il punto stazionario trovato è di minimo assoluto.
In conclusione, la funzione \(f(x,y)\) ha punto di minimo assoluto in \(x=1\) e \(y=\frac1x=1\), e non possiede massimo assoluto. Tra tutti i rettangoli di area fissata, quello avente (semi-) perimetro minimo è il quadrato (\(x=y=1\)), mentre non ha senso chiedersi quale sia quello con (semi-)perimetro massimo perché facendo tendere la lunghezza \(x\) di uno dei due lati a \(0\), l’altro, di lunghezza \(y=1/x\), diventerà arbitrariamente lungo (facendo tendere il semiperimetro a \(+\infty\)).
Schema di risoluzione completo di una ottimizzazione su un insieme vincolato con vincoli sostituibili (B):
si controlla che il vincolo o i vincoli possano essere sostituiti facilmente nella funzione obiettivo (caso B), in modo da ottenere una funzione di una variabile;
se possibile, si disegna il dominio di ottimizzazione come sottoinsieme del piano cartesiano;
si effettua la sostituzione più semplice, identificando il dominio di ottimizzazione dove varia la variabile rimanente;
si risolve il corrispondente problema ad una dimensione.
Example 9.18 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione \[ f(x,y)=2x^2+y^2+1, \quad \text{sull'insieme} \quad A=\{ x^2+y-3=0\}. \] Il vincolo è rappresentato dalla parabola \(y=3-x^2\).
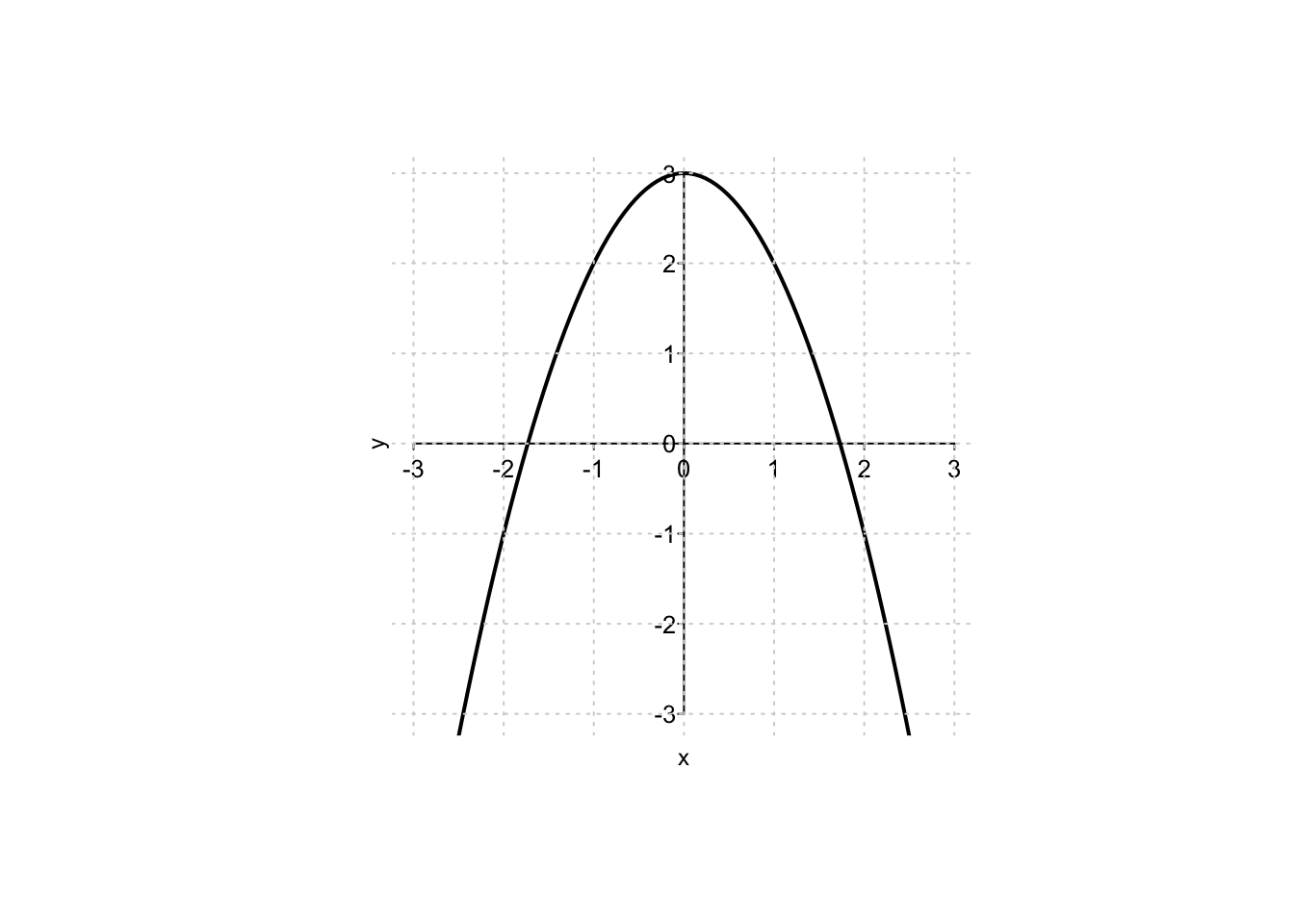
Si osservi che il vincolo può essere sostituito nella funzione. Nel farlo, si deve anche osservare che la sostituzione \(x^2=3-y\) risulta molto più semplice, e trasforma il problema in \[ \max,\,\min\, 2(3-y)+y^2+1=y^2-2y+7, \quad \text{sull'insieme} \quad A_y=(-\infty,3]. \] La funzione da ottimizzare è una parabola convessa. In quanto tale, sull’intervallo \((-\infty,3]\), non ha massimo assoluto (per \(x \to -\infty\) tende a diventare arbitrariamente grande) mentre ha minimo assoluto nel vertice (se appartenente ad \(A_y\)), oppure sul punto di frontiera \(x=3\). Il vertice è situato nel punto \(y=1\) che, essendo compreso nell’intervallo, rappresenta il punto di minimo assoluto della funzione. Ad \(y=1\) corrispondono i valori \(x^2=3-y=2\), ovvero \(x= \pm \sqrt{2}\).
In conclusione, la funzione \(f(x,y)\) non ha (punto di) massimo e possiede i punti di minimo assoluto \((-\sqrt{2},1)\) e \((\sqrt{2},1)\).
9.7 Il metodo dei moltiplicatori di Lagrange (C)
Nel caso in cui si ottimizzi una funzione su un dominio di ottimizzazione definito da un solo vincolo di uguaglianza, il seguente teorema dà le condizioni necessarie affinché un punto sia di massimo o minimo relativo.
Theorem 9.5 (Teorema dei moltiplicatori di Lagrange) Si assuma che la funzione obiettivo \(f:\mathbb{R}^2 \to \mathbb{R}\) ammetta derivate parziali del primo ordine continue e che debba essere ottimizzata sull’insieme \[ A=\{(x,y) \in \mathbb{R}^2: g(x,y)=0\}, \] con \(g:\mathbb{R}^2 \to \mathbb{R}\) che ammette anch’essa derivate parziali del primo ordine continue. Allora, i punti di massimo/minimo (relativi o assoluti) di \(f\) (nel caso esistano) sull’insieme \(A\), sono necessariamente punti stazionari della funzione lagrangiana \[ L:\mathbb{R}^3 \to \mathbb{R}, \quad L(x,y,\lambda)= f(x,y)- \lambda \,g(x,y). \]
Remark. Osserviamo i seguenti punti fondamentali sul Teorema dei moltiplicatori di Lagrange:
la incognita \(\lambda\) è detta moltiplicatore di Lagrange;
il metodo dei moltiplicatori di Lagrange funziona nei punti stazionari trovati se su di essi non si annullano entrambe le derivate parziali \(\frac{\partial g}{\partial x}\) e \(\frac{\partial g}{\partial y}\) (questa condizione tecnica sarà sempre verificata nel seguito);
nel caso in cui l’insieme \(A\) sia determinato da più vincoli di uguaglianza, le condizioni del teorema sono analoghe, con la presenza di un numero di moltiplicatori di Lagrange pari al numero dei vincoli (il metodo è in generale valido se il numero dei vincoli è inferiore a quello delle variabili);
come tutte le condizioni del primo ordine, ovvero basate esclusivamente sulle derivate prime, quelle enunciate nel teorema sono solo necessarie ma non sufficienti a garantire che i punti trovati siano effettivamente di massimo/minimo. È possibile enunciare anche delle condizioni sufficienti del secondo ordine ma esse si basano sulla convessità della funzione lagrangiana, ovvero di una funzione a tre variabili, e quindi vanno oltre gli scopi di questo corso (così come la dimostrazione della validità del metodo dei moltiplicatori);
come vedremo negli esempi seguenti, trovare i punti stazionari della funzione lagrangiana significa risolvere un sistema (non necessariamente lineare) a tre variabili e tre incognite, per cui non esiste un metodo generale di risoluzione;
per utilizzare il Teorema, si deve scrivere il vincolo della forma \(g(x,y)=0\); ad esempio, il vincolo \(x^2+3x=4\) dovrà essere scritto come \(x^2+3x-4=0\);
in alcuni libri di testo, la funzione lagrangiana è definita come \[ L(x,y,\lambda)= f(x,y)+ \lambda \,g(x,y), \] invertendo quindi il segno del moltiplicatore di Lagrange. Nulla cambia ai fini dell’ottimizzazione.
Come in generale accade per i teoremi basati esclusivamente su derivate del primo ordine, il Teorema dei moltiplicatori di Lagrange dà condizioni solo necessarie per un punto di massimo/minimo. È quindi richiesto uno sforzo aggiuntivo per determinare l’esatta natura dei punti trovati.
In tali casi è utile determinare l’esistenza del massimo/minimo della funzione obiettivo attraverso il Teorema di Weierstrass enunciato nel Capitolo 5, che è valido sotto le stesse ipotesi anche nel caso bivariato. Per enunciarlo in più dimensioni, è sufficiente definire il concetto di insieme limitato.
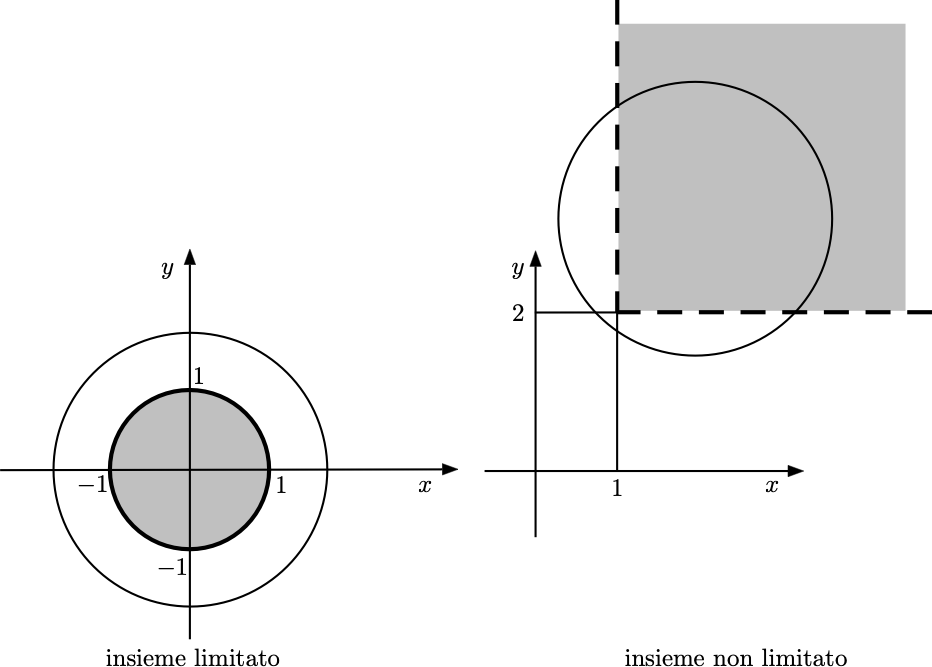
Definition 9.10 Un insieme \(A \subseteq \mathbb{R}^2\) è detto limitato se è possibile trovare un intorno \(I(x,y)\) di raggio \(r\) che lo contiene: \(A \subseteq I(x,y)\).
La definizione di insieme limitato è molto semplice ed intuitiva: un insieme è limitato se lo si può racchiudere dentro un cerchio; si veda la figura seguente.
Se riconoscere un insieme limitato è immediato, grazie al seguente teorema è molto semplice anche stabilire quando un insieme è chiuso.
Theorem 9.6 Data una funzione continua \(h:A \subseteq \mathbb{R}^2 \to \mathbb{R}\), e un numero \(k \in \mathbb{R}\), gli insiemi \[\begin{align*} A&=\{(x,y)\in \mathbb{R}^2 : h(x,y) = k\}, \\ \\ B&=\{(x,y)\in \mathbb{R}^2 : h(x,y) \geq (\leq) \,k\} \end{align*}\] sono chiusi.
Siamo quindi pronti per enunciare il teorema di Weierstrass.
Theorem 9.7 (Teorema di Weierstrass) Una funzione \(f:A \subseteq \mathbb{R}^2 \to \mathbb{R}\) continua su un insieme \(A\) non vuoto, chiuso e limitato, ammette sia massimo che minimo assoluti.
Si può quindi usare il Teorema dei moltiplicatori di Lagrange in abbinamento col Teorema di Weierstrass per risolvere alcuni problemi di ottimizzazione vincolata, come illustrato negli esempi seguenti.
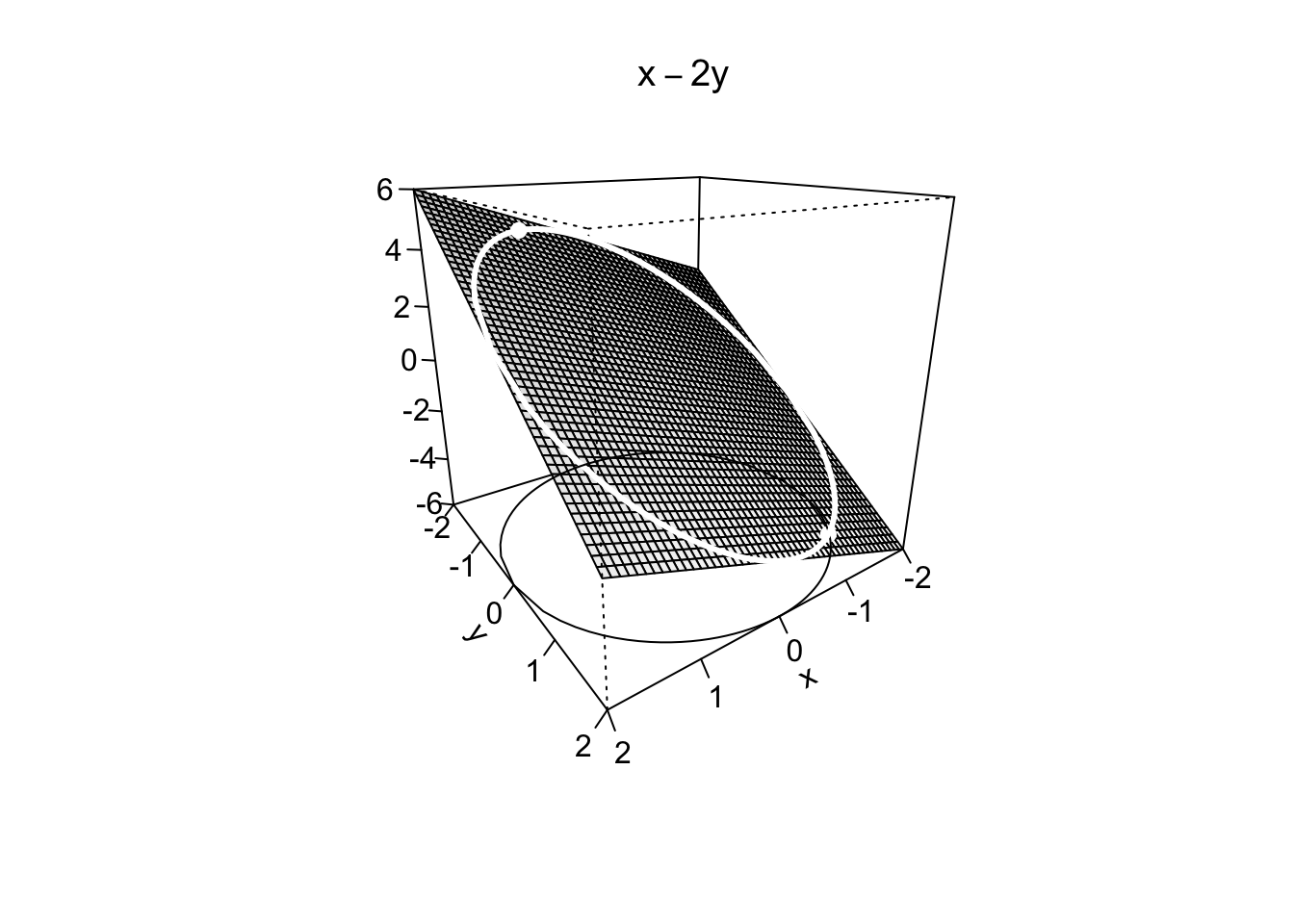
Example 9.19 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[ f(x,y)=x-2y, \quad \text{ sull'insieme } \quad A=\{x^2+y^2-4=0\}. \] L’insieme \(A\) è rappresentabile sul piano cartesiano come la circonferenza di centro l’origine e raggio pari a 2, ma l’equazione che lo definisce non è di facile sostituzione nella funzione obiettivo per ottenere una funzione univariata. Si può quindi cercare di operare tramite il Teorema dei moltiplicatori di Lagrange.
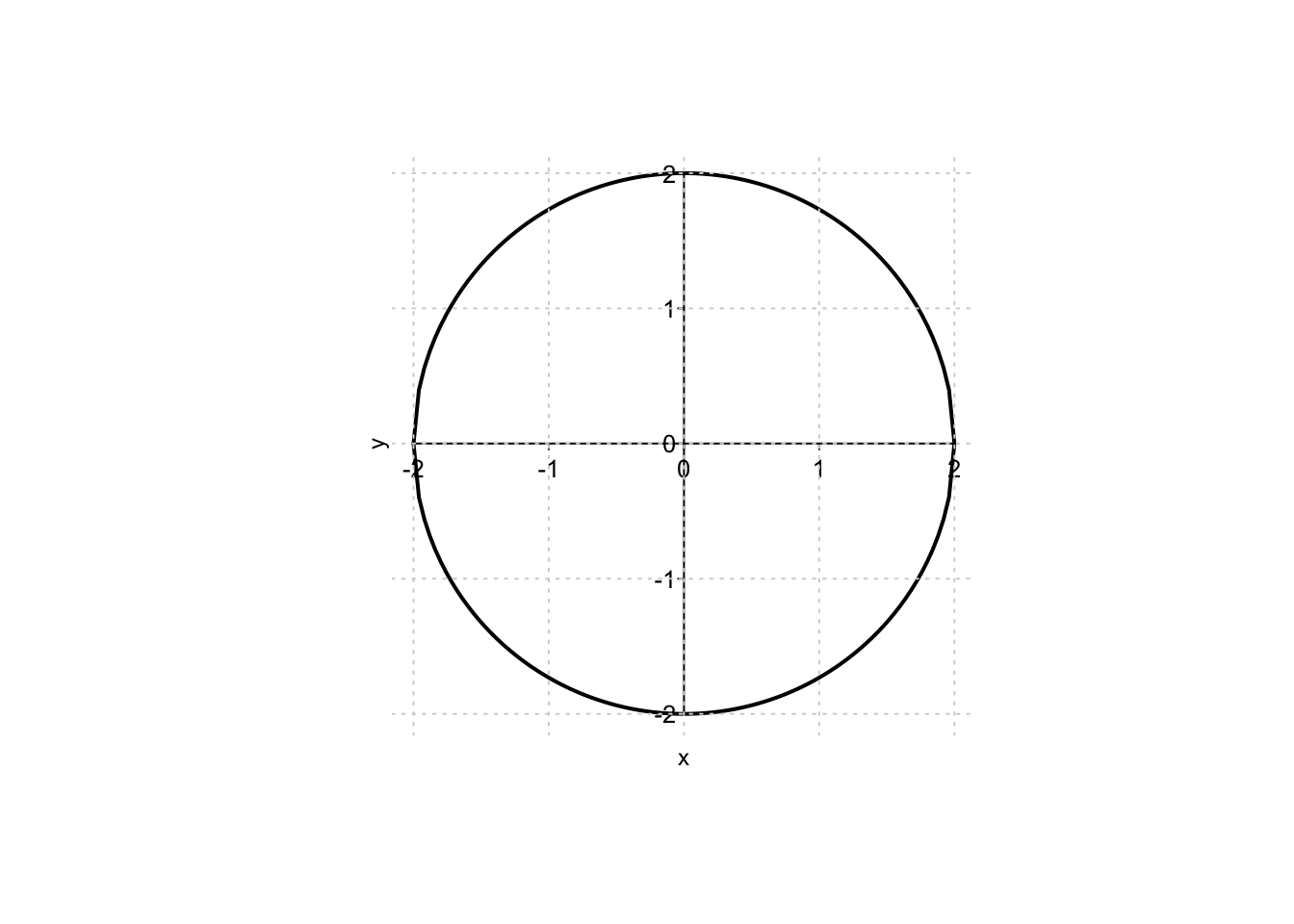
L’insieme \(A\) è limitato (perché contenuto ad esempio nel cerchio di raggio 3) e chiuso (essendo definito dall’equazione \(x^2+y^2=4\)). Essendo la funzione obiettivo continua, vale il Teorema di Weierstrass, e quindi esistono sia massimo che minimo assoluti. Questa è una informazione rilevante: tra i punti candidati soluzioni del sistema delle condizioni di Lagrange, dovranno necessariamente esserci i punti di massimo/minimo della funzione.
I punti stazionari della funzione lagrangiana \(L(x,y,\lambda)= f(x,y)- \lambda \,g(x,y)\), con \(g(x,y)=x^2+y^2-4\), sono dati dalle soluzioni del sistema
\[\begin{equation} \begin{cases} \frac{\partial L}{\partial x}=1-2\lambda\,x =0, \\ \frac{\partial L}{\partial y}=-2-2\lambda\,y=0, \\ \frac{\partial L}{\partial \lambda}=4-x^2-y^2=0. \end{cases} \tag{9.2} \end{equation}\]
Si osservi che l’ultima equazione del sistema dato dall’annullamento delle derivate parziali della funzione lagrangiana è il vincolo del problema di ottimizzazione.
Pur non esistendo un metodo generale di risoluzione del sistema (9.2), di solito si ricava il moltiplicatore di Lagrange dalle prime due equazioni, e quindi si sostituisce l’equazione trovata nella terza.
Dalle prime due equazioni si osserva che deve necessariamente essere \(x,y \neq 0\). Si può quindi ricavare \(\lambda\) da esse: \[ \lambda=\frac{1}{2x}=\frac{-2}{2y}, \] e sostituire \(y=-2x\) nel vincolo, ricavando \[ x^2+4x^2= 5x^2=4 \quad \Rightarrow \quad x=\pm \frac{2}{\sqrt{5}}, \] da cui si ottengono i due punti stazionari (per la lagrangiana) \[ \left(\frac{2}{\sqrt{5}},-\frac{4}{\sqrt{5}}\right)\overset{f}{\to}\frac{10}{\sqrt{5}}=2\sqrt{5},\quad \left(-\frac{2}{\sqrt{5}},\frac{4}{\sqrt{5}}\right)\overset{f}{\to}\frac{-10}{\sqrt{5}}=-2\sqrt{5}. \] Essendoci solo due punti candidati ad essere massimo e minimo, e sapendo che la funzione ammette massimo e minimo, dovrà necessariamente essere punto di massimo assoluto quello dove la funzione ammette valore più grande, e punto di minimo assoluto quello dove la funzione ammette valore più piccolo.
In conclusione \(\left(\frac{2}{\sqrt{5}},-\frac{4}{\sqrt{5}}\right)\) è punto di massimo assoluto, \(\left(-\frac{2}{\sqrt{5}},\frac{4}{\sqrt{5}}\right)\) è punto di minimo assoluto.
Schema di risoluzione completo di una ottimizzazione con un vincolo di \(=\) (C):
si controlla che il vincolo non sia facilmente sostituibile nella funzione obiettivo, in modo da ottenere una funzione di una variabile (e ricondursi al caso B);
si controlla la validità del Teorema di Weierstrass (altrimenti non sarà possibile determinare la natura delle soluzioni eventualmente trovate);
si trovano eventuali punti candidati a punti di massimo/minimo tra i punti stazionari della funzione lagrangiana;
se la funzione ammette massimo/minimo, si valuta la funzione su tutti i punti candidati: i punti di massimo (minimo) assoluto saranno i punti candidati dove la funzione assume valore più grande (piccolo).
Example 9.20 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[ f(x,y)=2x^2+2y^2, \quad \text{ sull'insieme } \quad A=\left\{x^2+xy+y^2=1\right\}. \] L’insieme \(A\) è rappresentabile sul piano cartesiano come l’ellisse seguente.
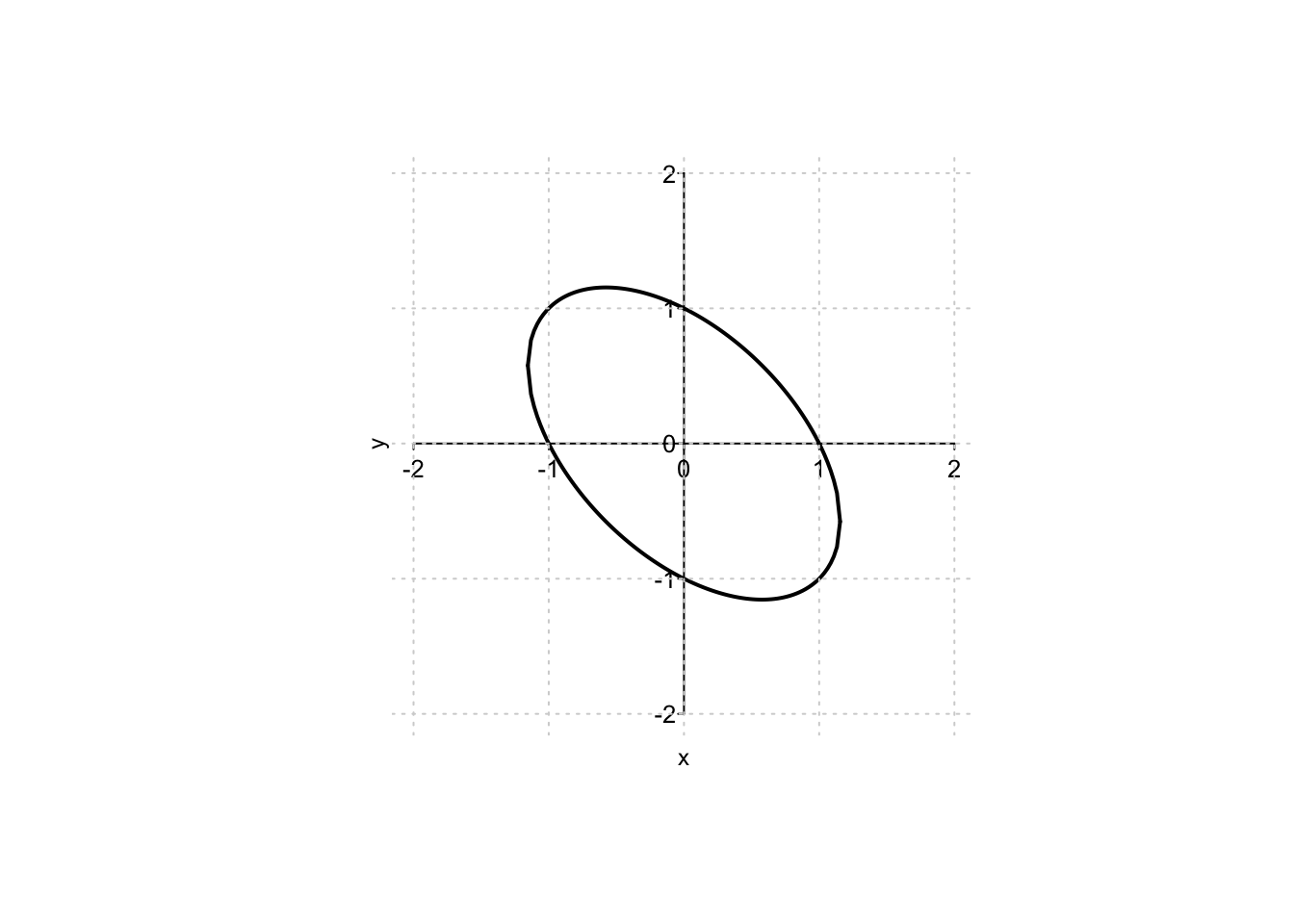 L’equazione che definisce l’ellisse non è di facile sostituzione nella funzione obiettivo per ottenere una funzione univariata, ma si osserva che l’insieme \(A\) è chiuso e limitato.
Essendo la funzione obiettivo continua, vale il Teorema di Weierstrass, quindi esistono sia massimo che minimo assoluti. Questa è una informazione rilevante: possiamo applicare il Teorema dei moltiplicatori di Lagrange e, tra i punti candidati trovati,
dovranno necessariamente esserci i punti di massimo/minimo della funzione.
L’equazione che definisce l’ellisse non è di facile sostituzione nella funzione obiettivo per ottenere una funzione univariata, ma si osserva che l’insieme \(A\) è chiuso e limitato.
Essendo la funzione obiettivo continua, vale il Teorema di Weierstrass, quindi esistono sia massimo che minimo assoluti. Questa è una informazione rilevante: possiamo applicare il Teorema dei moltiplicatori di Lagrange e, tra i punti candidati trovati,
dovranno necessariamente esserci i punti di massimo/minimo della funzione.
I punti stazionari della funzione lagrangiana \(L(x,y,\lambda)= f(x,y)- \lambda \,g(x,y)\), con \(g(x,y)=x^2+xy+y^2-1\), sono dati quindi dalle soluzioni del sistema
\[\begin{equation*} \begin{cases} \frac{\partial L}{\partial x}=4x-\lambda\,(2x+y) =0, \\ \frac{\partial L}{\partial y}=4y-\lambda\,(2y+x) =0, \\ \frac{\partial L}{\partial \lambda}= 1-x^2-xy-y^2 =0. \end{cases} \end{equation*}\]
Se fosse \((2x+y) = 0\), allora sarebbe anche \(x=0\), e di conseguenza \(y=-2x=0\). Il punto \((0,0)\) però non soddisfa il vincolo (terza equazione), ovvero non fa parte dell’insieme di ottimizzazione (l’ellisse). Analogamente, non può essere \((2y+x) = 0\).
Assumendo dunque \((2y+x) \neq 0\), e ricavando il moltiplicatore dalle prime due equazioni, si ottiene \[ \lambda=\frac{4x}{2x+y}=\frac{4y}{2y+x} \quad \Rightarrow \quad \frac{x}{2x+y}=\frac{y}{2y+x}, \] da cui si ricava \[ 2xy+x^2-2xy-y^2=x^2-y^2=0. \] Si ricava dunque \(x^2=y^2\), ovvero \(y = \pm x\). Si hanno allora i seguenti due casi:
- sostituendo nel vincolo \(y=x\), si ottiene \[ x^2+x\,x+x^2=3x^2=1 \quad \Rightarrow \quad x=\pm\frac{\sqrt{3}}{3}, \] e quindi si trovano i due punti stazionari \[ \left(\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}\right), \quad \left(-\frac{\sqrt{3}}{3},-\frac{\sqrt{3}}{3}\right); \]
- sostituendo nel vincolo \(y=-x\), si ottiene \[ x^2-x\,x+x^2=x^2=1 \quad \Rightarrow \quad x^2=\pm1, \] e quindi si trovano i due punti stazionari \[ \left(1,-1\right), \quad \left(-1,1\right). \]
Dato che massimo e minimo assoluti della funzione esistono per il Teorema di Weierstrass, ed essi devono forzatamente essere raggiunti sui punti candidati, basta valutare la funzione sui punti trovati \[ f\left(\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}\right)=\frac43, \quad f\left(-\frac{\sqrt{3}}{3},-\frac{\sqrt{3}}{3}\right)=\frac43, \quad f\left(1,-1\right)=4, \quad f\left(-1,1\right)=4. \] per determinare che i primi due punti sono punti di minimo assoluto, gli altri due punti di massimo assoluto.
Example 9.21 Si studi il classico problema economico del consumatore che ha a disposizione una somma \(k>0\) per acquistare le quantità \(x\) ed \(y\) di due beni dal prezzo unitario \(p_x>0\) e \(p_y>0\). Il consumatore basa la sua scelta sulla sua funzione di utilità \(u(x,y)\) che determina il livello di “soddisfazione” che riceve dal consumare le quantità \((x,y)\) dei due beni. Avendo a disposizione una somma limitata, il consumatore è sottoposto al vincolo di bilancio \[ \{p_x\,x+ p_y\, y \leq k\}. \] Assumendo \(u(x,y)\) strettamente crescente in entrambe le variabili \(x\) ed \(y\), il consumatore spenderà tutta la somma a disposizione, sottoponendosi al vincolo \[ \{p_x\,x+ p_y\, y = k\}. \] Ignorando al momento il vincolo di non negatività di \(x\) ed \(y\), quindi assumendo che il consumatore possa anche vendere sul mercato i due beni agli stessi prezzi, si deve studiare il problema \[ \max \, u(x,y), \quad \text{ sull'insieme } \quad \{p_x\,x+ p_y\, y-k=0\}. \] Assumendo che \(u(x,y)\) ammetta derivate parziali continue, la funzione lagrangiana ha espressione \[ L(x,y,\lambda)=u(x,y)-\lambda(p_x\,x+ p_y\, y-k), \] mentre i suoi punti stazionari sono le soluzioni del sistema \[\begin{equation} \begin{cases} \frac{\partial L}{\partial x}=\frac{\partial u}{\partial x}(x,y)-\lambda \,p_x=0, \\ \frac{\partial L}{\partial y}=\frac{\partial u}{\partial y}(x,y)-\lambda \,p_y=0, \\ \frac{\partial L}{\partial \lambda}=k-p_x\,x- p_y\, y=0. \end{cases} \tag{9.3} \end{equation}\]
Ricavando il moltiplicatore di Lagrange dalle prime due equazioni, e quindi sostituendo l’equazione così trovata nella terza, si ottiene la condizione necessaria: \[ \lambda=\frac{\frac{\partial u}{\partial x}(x,y)}{p_x}=\frac{\frac{\partial u}{\partial y}(x,y)}{p_y}, \] ovvero, se \(\frac{\partial u}{\partial x}(x,y),\frac{\partial u}{\partial y}(x,y) \neq 0\), si ha che \[ \frac{p_x}{p_y}=\frac{\frac{\partial u}{\partial x}(x,y)}{\frac{\partial u}{\partial y}(x,y)}. \] In Economia si dice che il tasso (saggio) marginale di sostituzione (il membro di destra dell’equazione precedente) deve essere uguale al rapporto dei prezzi dei due beni. Questa è una condizione necessaria alla massimizzazione dell’utilità del consumatore.
Riprendendo l’Esempio 9.16, se \(u(x,y)=xy\), si ha che (se \(x,y \neq 0\)) \[ \frac{p_x}{p_y}=\frac{y}{x}, \] che sostituita (\(y=x\,\frac{p_x}{p_y}\)) nel vincolo di bilancio dà l’equazione \[ p_x \, x +p_y\,x\,\frac{p_x}{p_y}= 2p_x\,x=k, \] ovvero \(x=\frac{k}{2 p_x}\), che implica \(y=x\,\frac{p_x}{p_y}=\frac{k}{2 p_x}\frac{p_x}{p_y}=\frac{k}{2 p_y}\). Per \(x,y \neq 0\), si ha dunque il punto stazionario \(\left(\frac{k}{2 p_x},\frac{k}{2 p_y}\right)\).
Se \(x=0\), allora dalla seconda equazione di (9.3) si ricava \(\lambda=0\) e quindi, dalla prima, \(y=0\). Il punto \((0,0)\) non è però ammissibile nel vincolo di bilancio.
L’unica possibile soluzione del problema vincolato è quindi \(\left(\frac{k}{2 p_x},\frac{k}{2 p_y}\right)\), che è stata dimostrata nell’Esempio 9.16 essere un punto di massimo assoluto (per \(p_x=p_y=k=1\)).
9.8 Massimo e minimo su dominio chiuso e limitato (D)
In generale, per quanto riguarda l’ottimizzazione di funzioni di due variabili, si può affermare quanto già detto per le funzioni di una variabile.
Una funzione \(f:A\subseteq \mathbb{R}^2 \to \mathbb{R}\) può avere massimo/minimo assoluto:
nei punti stazionari interni al suo dominio;
nei punti di frontiera inclusi nel suo dominio.
Questa affermazione vale in generale per l’ottimizzazione di funzioni di \(n\) variabili. Tutti gli schemi di risoluzione trattati in questo capitolo si estendono analogamente per funzioni di \(n\) variabili con domini di ottimizzazione definiti da un numero finito di vincoli.
Se \(A\) è un insieme chiuso e limitato ed \(f\) è continua, l’esistenza di massimo e minimo è garantita dal Teorema di Weierstrass.
L’unica differenza nell’ottimizzazione di funzioni di una variabile o di due variabili è la differente natura dei domini di ottimizzazione: è naturalmente più complesso ottimizzare su un dominio multidimensionale.
Schema di risoluzione completo di ottimizzazione in un dominio chiuso e limitato (definito da più vincoli) (D):
si controlla la validità del Teorema di Weierstrass per poter stilare una lista di punti candidati tra i quali poter certamente trovare i punti di massimo/minimo;
si cercano punti candidati a massimo/minimo tra eventuali punti stazionari interni del dominio di ottimizzazione, uguagliando a zero le due derivate parziali della funzione e calcolando la matrice Hessiana per determinare la natura dei punti;
si cercano altri punti candidati tra i punti di frontiera inclusi nel dominio, riducendo la funzione a univariata o utilizzando il Teorema dei moltiplicatori di Lagrange;
se la funzione ammette massimo/minimo, si valuta la funzione su tutti i punti candidati: i punti di massimo (minimo) assoluto saranno i punti candidati dove la funzione assume valore più grande (piccolo).
Example 9.22 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\)
\[
f(x,y)=-x^3+\frac52xy-y, \quad \text{ sull'insieme } \quad Q=\left\{0\leq x \leq 1, 0\leq y \leq 1\right\}.
\]
L’insieme \(Q\) è il quadrato unitario: è un insieme chiuso e limitato.
Essendo la funzione obiettivo continua, essa ammette massimo/minimo assoluto per il Teorema di Weierstrass.
 Si ricercano quindi punti candidati ad essere punti di massimo/minimo nei punti stazionari interni a \(Q\).
Calcolando le derivate parziali della funzione obiettivo e uguagliandole a zero, si ottiene il sistema
\[
\begin{cases}
\frac{\partial f}{\partial x}=-3x^2+\frac52y=0, \\
\frac{\partial f}{\partial y}=\frac52x-1=0,
\end{cases}
\]
da cui si trova l’unico punto stazionario \(\left(\frac25,\frac{24}{125}\right)\).
Essendo un punto interno al dominio (il punto appartiene all’interno del quadrato), è possibile calcolare
la matrice Hessiana:
\[
H_f(x,y)=\left(\begin{array}{cc}-6x & \frac52 \\ \frac52 & 0\end{array}\right).
\]
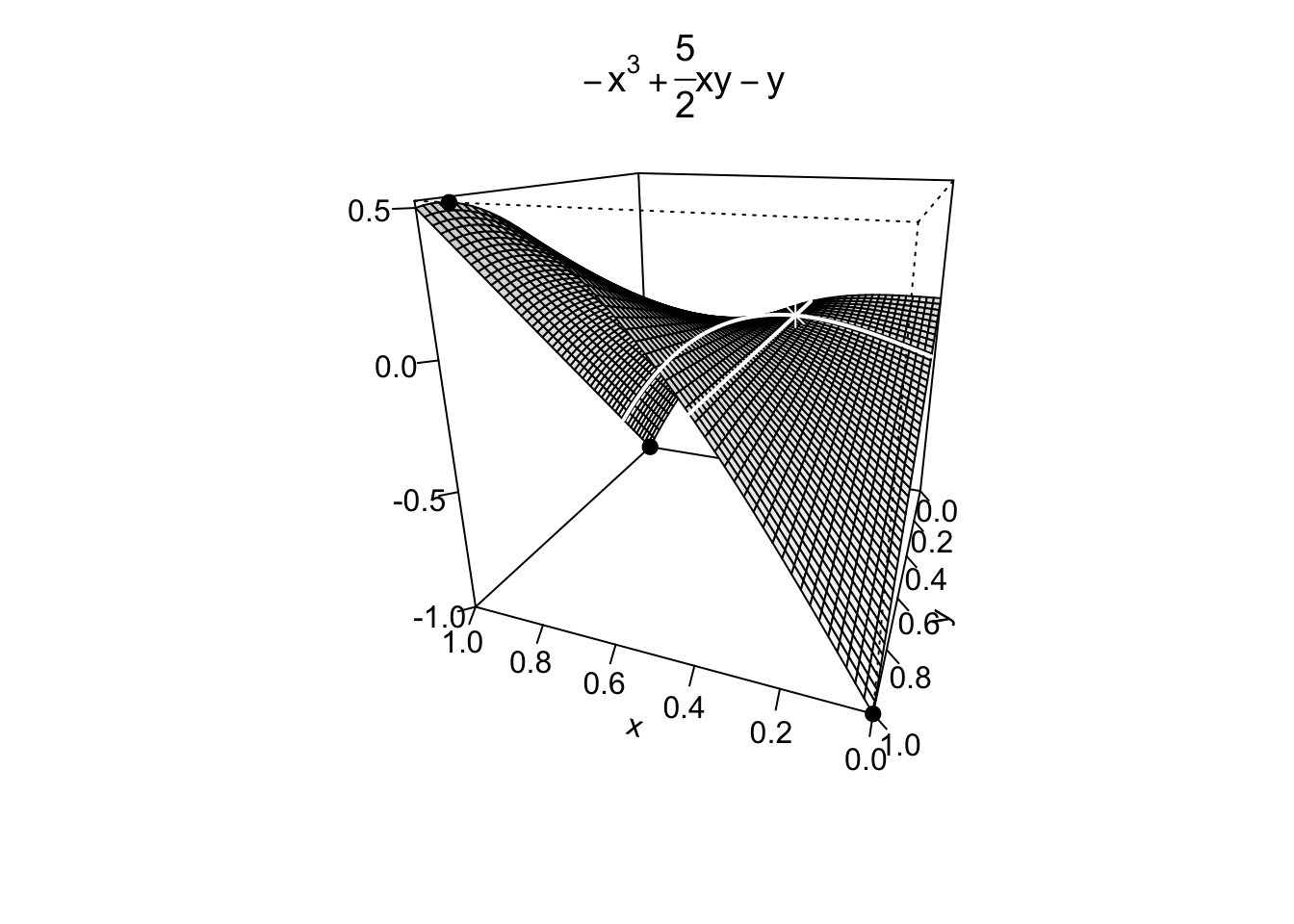
Si verifica che \(\text{det}( H_f(x,y)) <0\), quindi il punto trovato è un punto di sella.
Si ricercano quindi punti candidati ad essere punti di massimo/minimo nei punti stazionari interni a \(Q\).
Calcolando le derivate parziali della funzione obiettivo e uguagliandole a zero, si ottiene il sistema
\[
\begin{cases}
\frac{\partial f}{\partial x}=-3x^2+\frac52y=0, \\
\frac{\partial f}{\partial y}=\frac52x-1=0,
\end{cases}
\]
da cui si trova l’unico punto stazionario \(\left(\frac25,\frac{24}{125}\right)\).
Essendo un punto interno al dominio (il punto appartiene all’interno del quadrato), è possibile calcolare
la matrice Hessiana:
\[
H_f(x,y)=\left(\begin{array}{cc}-6x & \frac52 \\ \frac52 & 0\end{array}\right).
\]
Si verifica che \(\text{det}( H_f(x,y)) <0\), quindi il punto trovato è un punto di sella.
Requisito necessario per calcolare derivate del primo e secondo ordine in un punto è che il punto in questione sia interno al dominio nel quale lo si sta considerando. È quindi un errore grave procedere al calcolo della matrice Hessiana nei punti di frontiera del dominio di ottimizzazione.
I punti di massimo/minimo della funzione sono quindi localizzati sui quattro lati del quadrato \(A\), che costituiscono la frontiera del dominio di ottimizzazione. Su di essi, il comportamento della funzione va analizzato lato per lato:
LATO A) \(y=0, 0\leq x \leq 1\); La funzione diviene unidimensionale se considerata sull’intervallo \(x \in [0,1]\), ovvero \(f(x,0)=-x^3\). Questa è una funzione decrescente, che ha quindi massimo in \(x=0\) e minimo in \(x=1\). Nel lato A si avrà quindi il punto \((0,0) \overset{f}{\to} 0\) come candidato massimo, il punto \((1,0) \overset{f}{\to} -1\) come candidato minimo.
LATO B) \(x=0, 0\leq y \leq 1\); si ottimizza \(f(0,y)=-y,\, y \in [0,1]\). Anche in questo caso la funzione è decrescente, quindi ha massimo in \(y=0\) e minimo in \(y=1\). Nel lato B si avrà quindi il punto \((0,0)\) come candidato massimo (già considerato in A), il punto \((0,1) \overset{f}{\to} -1\) come candidato minimo.
LATO D) \(x=1, 0\leq y \leq 1\); si ottimizza \(f(1,y)=-1+\frac52 y - y=\frac32y-1,\, y \in [0,1]\). In questo caso, la funzione è crescente e ha massimo in \(y=1\) e minimo in \(y=0\). Nel lato D si avrà quindi il punto \((1,1) \overset{f}{\to} \frac12\) come candidato massimo, il punto \((1,0)\) come candidato minimo (già considerato in A).
LATO C) \(y=1, 0\leq x \leq 1\); si ottimizza \(f(x,1)=h(x)=-x^3+\frac52x-1,\, x \in [0,1]\). Questa funzione può avere punti di massimo/minimo agli estremi dell’intervallo \([0,1]\) (che corrispondono però a due vertici del quadrato che sono già stati considerati in precedenza), oppure in eventuali punti stazionari al suo interno. Si calcola dunque \(h'(x)=-3x^2+\frac52=0\), da cui si ricava la soluzione positiva \(x=\sqrt{\frac56}\). Per capire la natura di questo punto, si può studiare il segno della derivata prima o più velocemente calcolare \(h''(x)=-6x<0,\, x \in (0,1)\). Il punto in questione è quindi un candidato massimo. Inoltre, questo massimo, dovrà forzatamente superare il valore raggiunto agli estremi \((0,1) \overset{f}{\to} -1\) e \((1,1) \overset{f}{\to} \frac12\), e quindi sarà il punto di massimo assoluto della funzione.
Dato che la funzione ammette massimo e minimo, dalla analisi dei punti candidati risulta in conclusione che la funzione ha punto di massimo assoluto in \(\left(\sqrt{\frac56},1\right)\); punti di minimo assoluto in \((1,0)\) e \((0,1)\).
A meno che il testo dell’esercizio non lo richieda espressamente, non è necessario calcolare il valore raggiunto dalla funzione nei punti di massimo/minimo.
9.9 Esercizi riassuntivi
In alcuni casi particolari, l’ottimizzazione di una funzione di due variabili può essere semplificata. È quindi sempre raccomandabile studiare il problema in oggetto per trovare la strategia di risoluzione più veloce, e non svolgere meccanicamente i passi descritti in generale.
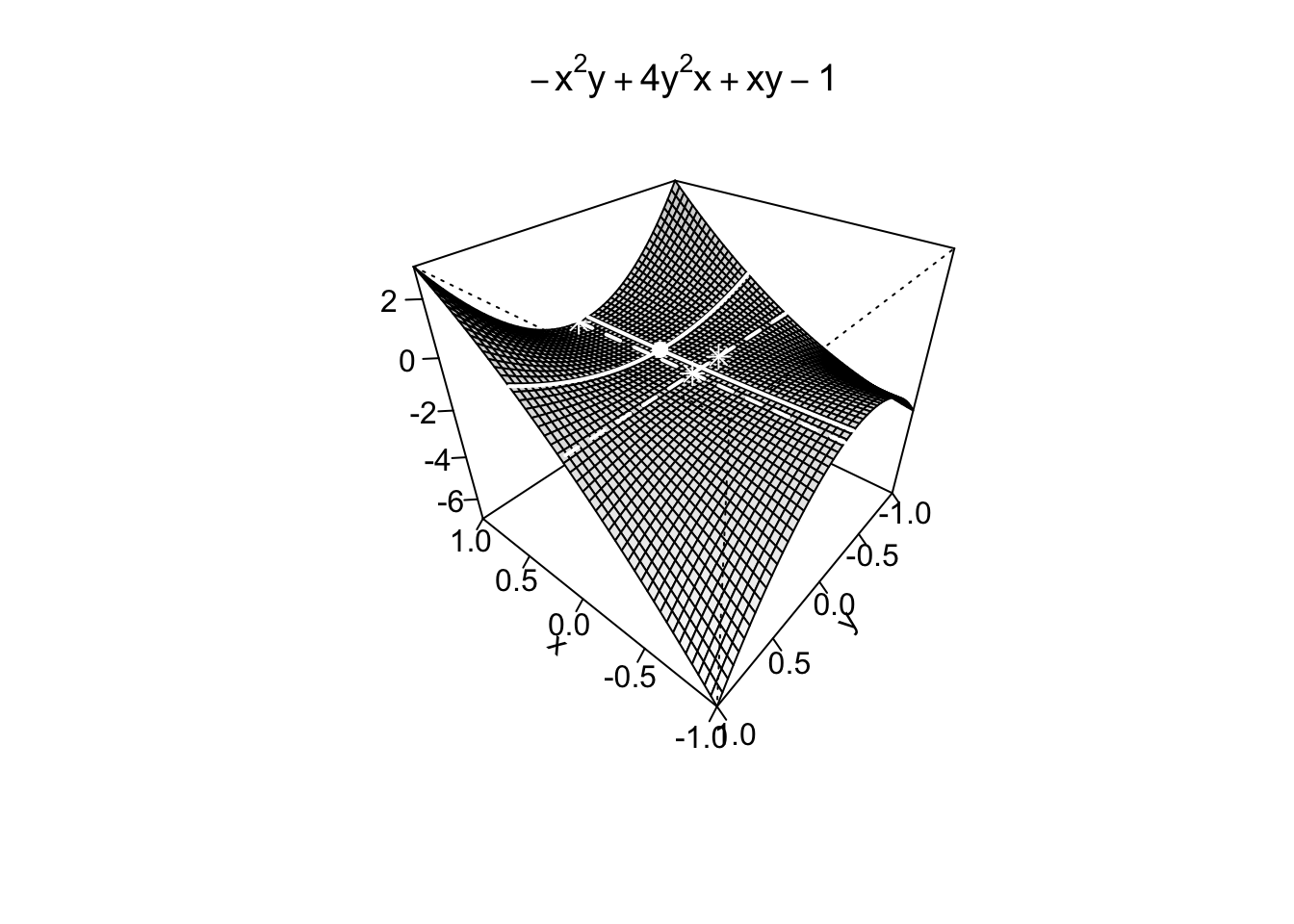
Example 9.23 Si trovino e si classifichino tutti i punti stazionari della funzione \(g:\mathbb{R}^2 \to \mathbb{R},\) definita da \[ g(x,y)=e^{-x^2y+4y^2x+xy-1}, \] indicando se essi sono punti di massimo/minimo assoluto o relativo oppure punti di sella.
È immediato osservare che la presenza dell’esponenziale, funzione strettamente crescente, naturalmente influenza il massimo/minimo della funzione ma non altera la localizzazione dei punti di massimo/minimo.
Si può quindi considerare la funzione \[ f(x,y)=-x^2y+4y^2x+xy-1. \] Si cercano i punti stazionari della funzione calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema: \[ \begin{cases} \frac{\partial f}{\partial x}=-2xy+4y^2+y=0, \\ \frac{\partial f}{\partial y}=-x^2+8xy+x=0. \end{cases} \quad \Rightarrow \quad \begin{cases} y\,(-2x+4y+1)&=0, \\ x\,(-x+8y+1)&=0. \end{cases} \] Per trovare tutti i punti stazionari, si discutono i seguenti casi sfruttando la legge di annullamento del prodotto:
se \(x=0\), dalla prima equazione si ricava: \[ y\,(4y+1)=0 \quad \Rightarrow \quad y=0,-\frac14. \] Si trovano quindi i due punti stazionari \((0,0)\) e \((0,-\frac14)\);
se \(y=0\), dalla seconda equazione si ricava: \[ x\,(-x+1) \quad \Rightarrow \quad x=0,1. \] Si trovano quindi i due punti stazionari \((0,0)\) (già considerato) e \((1,0)\);
nel caso rimanente, ovvero se \(x\neq 0\) e \(y \neq 0\), dalla legge di annullamento del prodotto applicata alle prime due equazioni si ricava il sistema lineare \[ \begin{cases} -2x+4y+1&=0, \\ -x+8y+1&=0, \end{cases} \] che ha come unica soluzione (si veda il Capitolo 7) il punto \(\left(\frac13, -\frac{1}{12}\right)\).
Per capire la natura dei quattro punti stazionari trovati, si calcola la matrice Hessiana \[ H_f(x,y)=\left(\begin{array}{cc}-2y & -2x+8y+1 \\ -2x+8y+1 & 8x\end{array}\right), \] e si procede applicando il Teorema 9.4.
In conclusione, \(f(x,y)\) non ammette massimo assoluto (altrimenti lo avremmo trovato tra i punti stazionari), e nemmeno minimo assoluto poiché \[ \lim_{x \to +\infty} f(x,1)=\lim_{x \to +\infty} -x^2+5x-1=-\infty. \]
Le stesse conclusioni valgono per \(g(x,y)=e^{f(x,y)}\).
Un altro caso facilmente risolvibile è quello in cui la funzione obiettivo sia a variabili separabili ovvero si possa esprimere come \[ f(x,y)=g(x)+h(y). \] In questo caso, è sufficiente ottimizzare separatamente le due funzioni \(g\) e \(h\) di una variabile, come nell’esempio seguente.
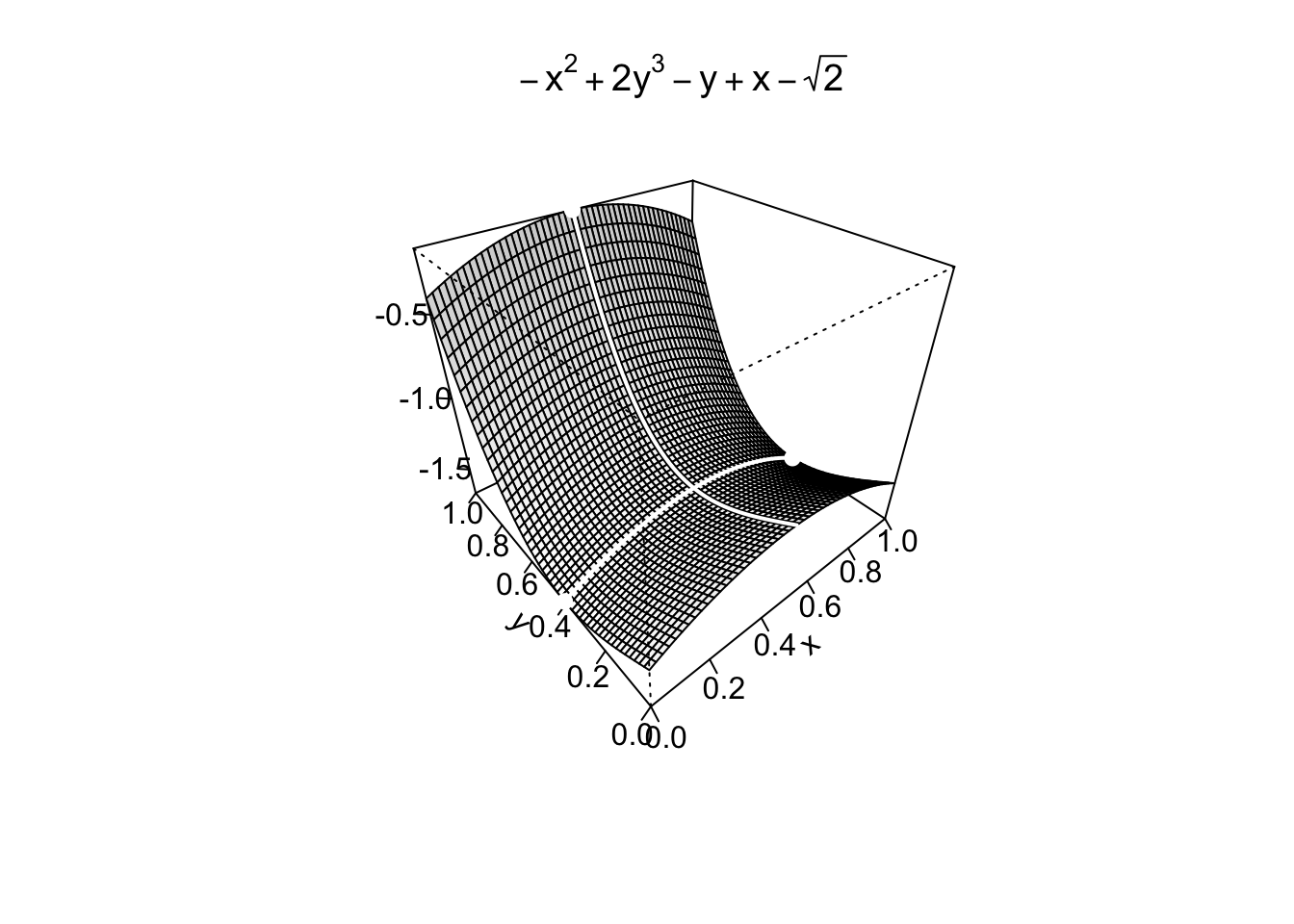
Example 9.24 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[ f(x,y)=-x^2+2y^3-y+x-\sqrt{2}, \quad \text{ sull'insieme } \quad Q=\left\{0\leq x \leq 1, 0\leq y \leq 1\right\}. \] L’insieme \(Q\) è il quadrato unitario: è un insieme chiuso e limitato. Essendo la funzione obiettivo continua, per il Teorema di Weierstrass essa ammette massimo e minimo assoluti.
È fondamentale osservare che la funzione \(f(x,y)\) può essere scritta come \[ f(x,y)= g(x)+h(y), \quad \text{ con } \quad g(x)=-x^2+x, \quad h(y)=2y^3-y-\sqrt2. \] Il massimo (minimo) di \(f\) è raggiunto in corrispondenza del massimo (minimo) di \(g\) e \(h\).
Per quanto riguarda \(g(x)=-x^2+x=x(-x+1), \, x \in [0,1]\), questa funzione è una parabola concava che ha punto di massimo in \(x=\frac12\) e punti di minimo in \(x=0,1\).
Per quanto riguarda \(h(y)=2y^3-y-\sqrt2, \, y \in [0,1]\), si ha \(h'(y)=6y^2-1=0\), per \(y=\frac{\sqrt6}{6}\), con \(h''(y)=12y>0\). \(h\) ha quindi punto di minimo in \(y=\frac{\sqrt6}{6}\) e punto di massimo in \(y=1\) (si osservi che \(h(1)>h(0)\)).
In conclusione, si ha che \(f(x,y)\) ha punti di minimo assoluto in \((0,\frac{\sqrt6}{6})\) e \((1,\frac{\sqrt6}{6})\); punto di massimo assoluto in \((\frac12, 1)\).
Concludiamo questa sezione con altri due esempi di ottimizzazione.
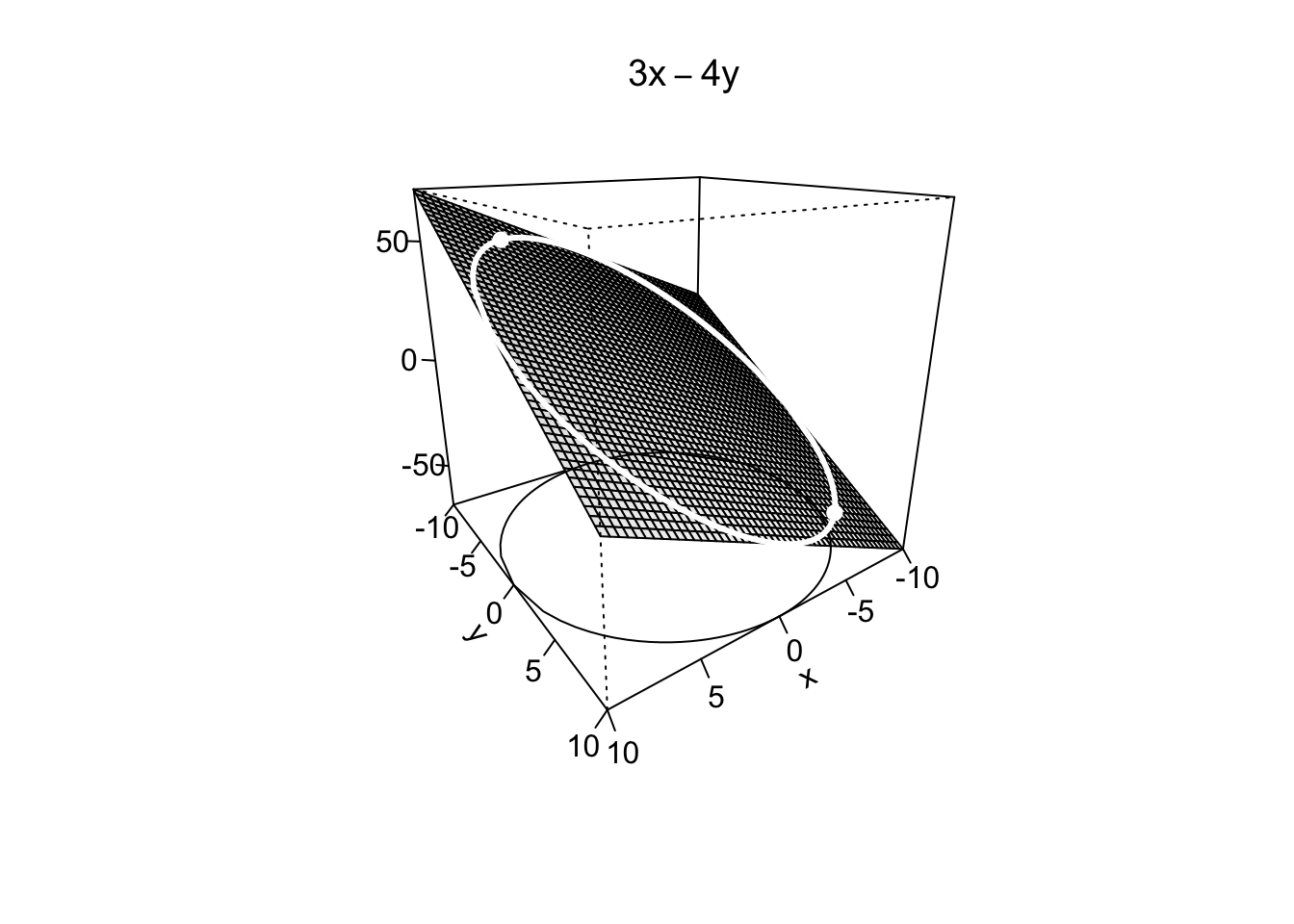
Example 9.25 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[ f(x,y)=3x-4y, \quad \text{ sull'insieme } \quad C=\{x^2+y^2=100\}. \] L’insieme \(C\) è rappresentabile sul piano cartesiano come la circonferenza di centro l’origine e raggio pari a 10, ma l’equazione che lo definisce non è di facile sostituzione nella funzione obiettivo per ottenere una funzione univariata. Si può cercare di operare tramite il Teorema dei moltiplicatori di Lagrange (C).
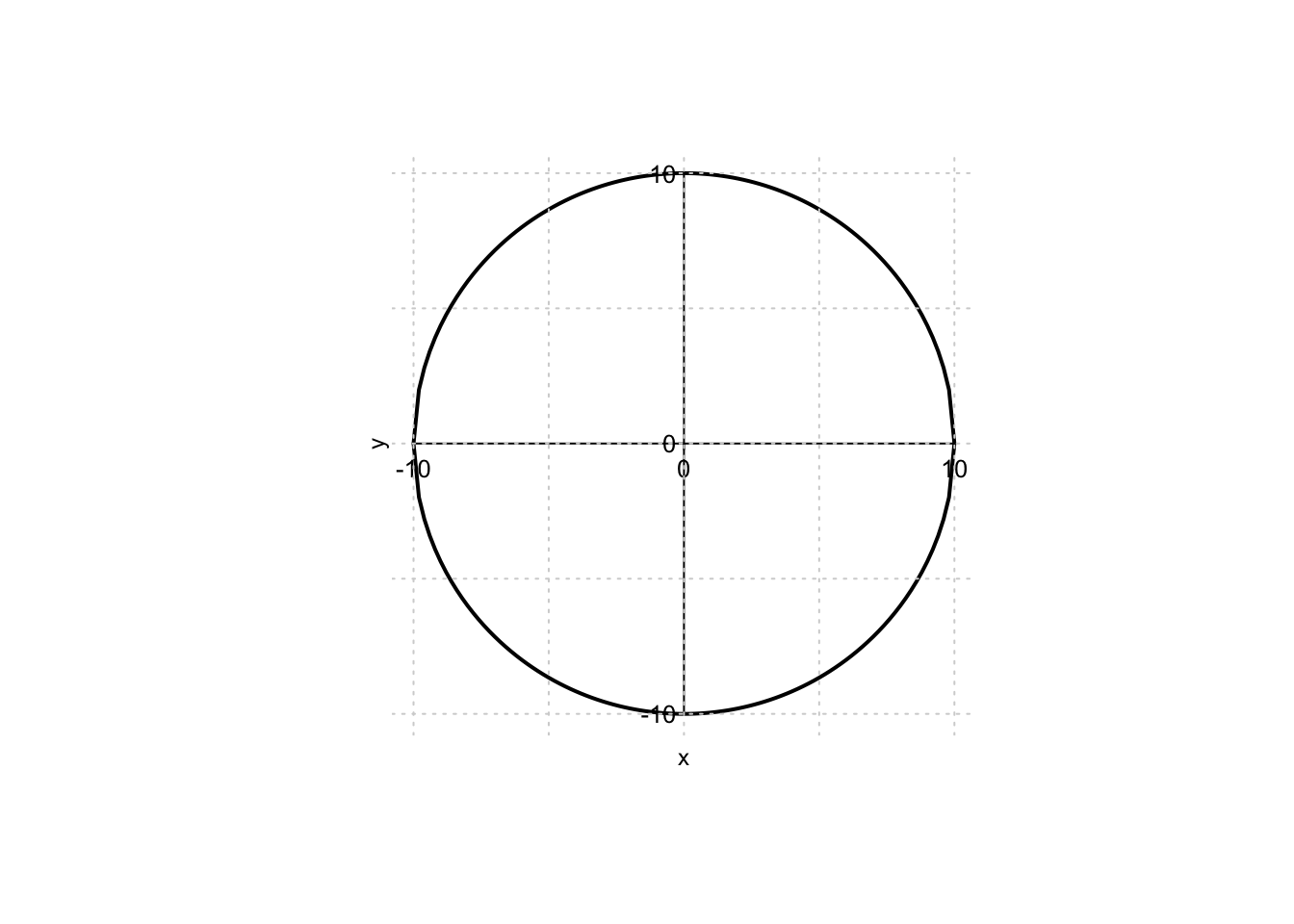
Essendo l’insieme \(C\) chiuso e limitato e la funzione obiettivo continua, vale il Teorema di Weierstrass, quindi esistono sia massimo che minimo assoluti. Questa è una informazione rilevante: tra i punti candidati soluzioni del sistema delle condizioni di Lagrange, dovranno necessariamente esserci i punti di massimo/minimo della funzione.
I punti stazionari della funzione lagrangiana \(L(x,y,\lambda)= f(x,y)- \lambda \,g(x,y)\) sono dati dalle soluzioni del sistema
\[\begin{equation*} \begin{cases} \frac{\partial L}{\partial x}=3-2\lambda\,x =0, \\ \frac{\partial L}{\partial y}=-4-2\lambda\,y=0, \\ \frac{\partial L}{\partial \lambda}=100-x^2-y^2=0. \end{cases} \end{equation*}\]
Dalle prime due equazioni si osserva che deve necessariamente essere \(x,y \neq 0\). Si può quindi ricavare \(\lambda\) da esse: \[ \lambda=\frac{3}{2x}=\frac{-2}{y}, \] e sostituire \(y=-\frac43 x\) nel vincolo, ricavando \[ x^2+\frac{16}{9}x^2= \frac{25}{9}x^2=100 \quad \Rightarrow \quad x=\pm \sqrt{36}=\pm 6, \] da cui, dalla relazione precedentemente trovata \(y=-\frac43 x\), si ottengono i due punti stazionari (per la lagrangiana) \[ \left(6,-8\right)\overset{f}{\to} 50 ,\quad \left(-6,8\right)\overset{f}{\to} -50. \] Essendoci solo due punti candidati ad essere massimo e minimo, e conoscendo che la funzione ammette massimo e minimo, dovrà necessariamente essere punto di massimo assoluto quello dove la funzione ammette valore più grande, punto di minimo assoluto quello dove la funzione ammette valore più piccolo.
In conclusione \(\left(6,-8\right)\) è punto di massimo assoluto, mentre \(\left(-6,8\right)\) è punto di minimo assoluto.
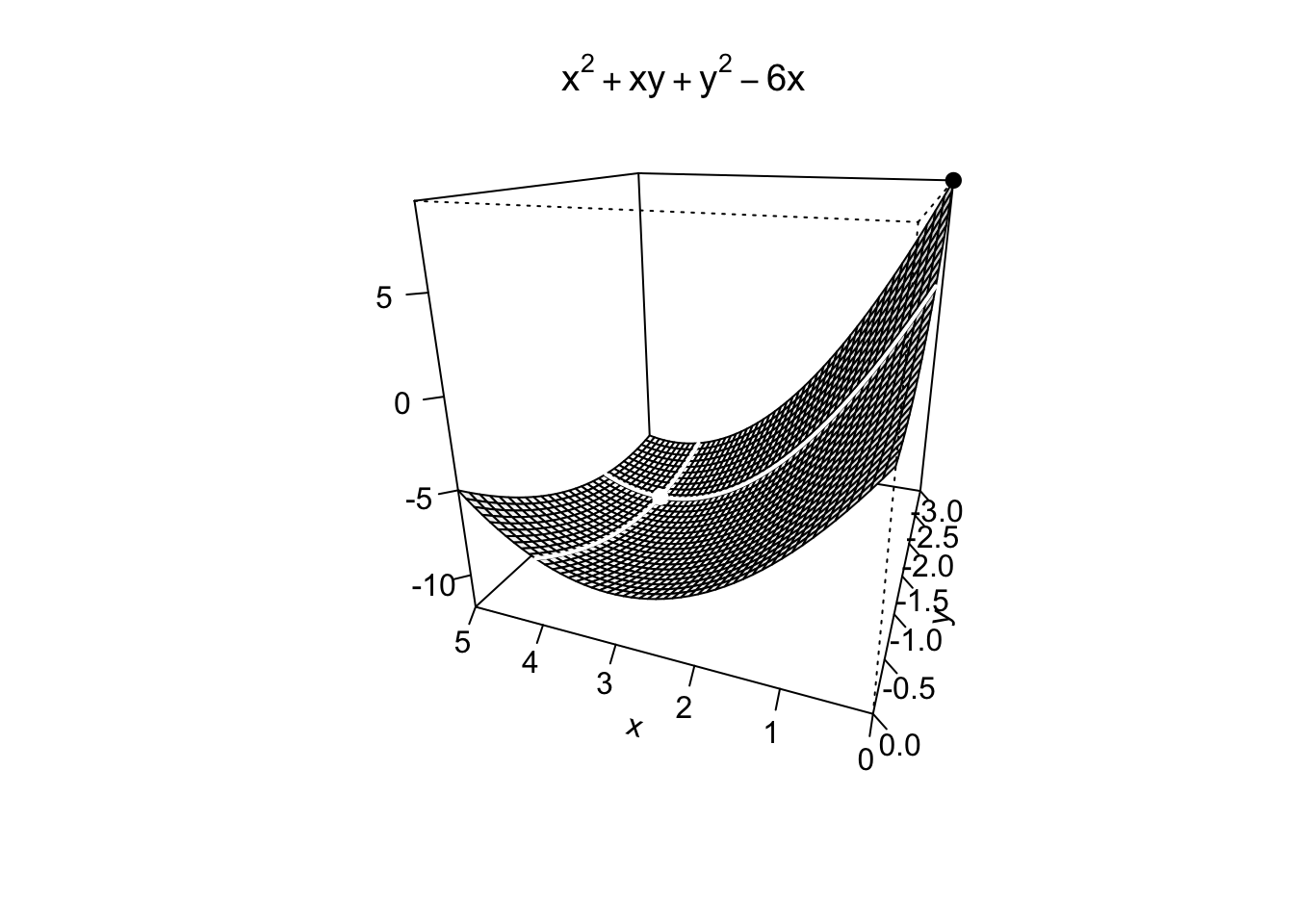
Example 9.26 Nel caso esistano, si trovino i punti di massimo/minimo assoluto della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\)
\[
f(x,y)=x^2+xy+y^2-6x, \quad \text{ sull'insieme } \quad R=\left\{0\leq x \leq 5, -3\leq y \leq 0\right\}.
\]
L’insieme \(R\) è un rettangolo, quindi è un insieme chiuso e limitato.
Essendo la funzione obiettivo continua, essa ammette massimo/minimo assoluti per il Teorema di Weierstrass.
 Si procede quindi come per la tipologia D
ricercando punti candidati ad essere punti di massimo/minimo nei punti stazionari interni a \(R\).
Calcolando le derivate parziali della funzione obiettivo e uguagliandole a zero, si ottiene il sistema
\[
\begin{cases}
\frac{\partial f}{\partial x}=2x+y-6=0, \\
\frac{\partial f}{\partial y}=x+2y=0,
\end{cases}
\]
risolvendo il quale si trova l’unico punto stazionario \(\left(4,-2\right)\).
Essendo un punto interno al dominio (il punto appartiene all’interno del rettangolo), è possibile calcolare
la matrice Hessiana:
\[
H_f(x,y)=\left(\begin{array}{cc}2 & 1 \\ 1 & 2\end{array}\right).
\]
Si verifica che \(\text{det} (H_f(x,y))=4-1=3 >0\), e \(\frac{\partial^2 f}{\partial x^2}=2>0\) per ogni \((x,y) \in \mathbb{R}^2\) quindi il punto trovato è un punto di minimo assoluto per la funzione \(f(x,y)\) considerata su tutto \(\mathbb{R}^2\).
A maggior ragione esso è punto di minimo assoluto su \(R \subseteq \mathbb{R}^2\).
Si procede quindi come per la tipologia D
ricercando punti candidati ad essere punti di massimo/minimo nei punti stazionari interni a \(R\).
Calcolando le derivate parziali della funzione obiettivo e uguagliandole a zero, si ottiene il sistema
\[
\begin{cases}
\frac{\partial f}{\partial x}=2x+y-6=0, \\
\frac{\partial f}{\partial y}=x+2y=0,
\end{cases}
\]
risolvendo il quale si trova l’unico punto stazionario \(\left(4,-2\right)\).
Essendo un punto interno al dominio (il punto appartiene all’interno del rettangolo), è possibile calcolare
la matrice Hessiana:
\[
H_f(x,y)=\left(\begin{array}{cc}2 & 1 \\ 1 & 2\end{array}\right).
\]
Si verifica che \(\text{det} (H_f(x,y))=4-1=3 >0\), e \(\frac{\partial^2 f}{\partial x^2}=2>0\) per ogni \((x,y) \in \mathbb{R}^2\) quindi il punto trovato è un punto di minimo assoluto per la funzione \(f(x,y)\) considerata su tutto \(\mathbb{R}^2\).
A maggior ragione esso è punto di minimo assoluto su \(R \subseteq \mathbb{R}^2\).
I punti di massimo della funzione sono invece localizzati sui quattro lati di \(R\), i punti di frontiera del dominio di ottimizzazione.
La funzione obiettivo è un polinomio di secondo grado in cui i coefficienti delle variabili di secondo grado sono positivi. Non è necessario quindi svolgere in dettaglio uno studio lato per lato come fatto nell’Esempio 9.22, perché sostituendo un valore qualsiasi ad una delle due variabili \(x\) o \(y\), si trova in ogni caso una parabola convessa (si può svolgere ad esempio il primo lato sostituendo \(y=0, \, 0\leq x \leq 5\)). Di conseguenza, il punto o i punti di massimo assoluto sono localizzati sui vertici del rettangolo. Per trovare esattamente dove, basta sostituire ad ognuno di essi il valore della funzione: \[ f(0,0)=0, \quad f(5,0)=-5, \quad f(0, -3)=9, \quad f(5,-3)=-11. \]
Dato che la funzione ammette massimo e minimo, dalla analisi dei punti candidati risulta in conclusione che la funzione ha punto di massimo assoluto in \((0,-3)\); punto di minimo assoluto in \((4,-2)\).
9.10 Il modello di regressione lineare
Il modello (di regressione) lineare è uno dei modelli matematici maggiormente utilizzati in Statistica. Il modello si utilizza nell’ipotesi di una relazione di dipendenza funzionale (lineare) tra due variabili, che permetta di prevedere il valore di una in funzione del valore assunto dall’altra.
Si assuma di avere un numero \(n\in \mathbb{N}, \, n>1,\) di osservazioni \(x_i,y_i,\, 1 \leq i \leq n,\) relative a due variabili \(X\) (variabile indipendente) ed \(Y\) (variabile dipendente).
Ad esempio, si supponga di voler ricavare una relazione lineare tra il peso (\(Y\), in kg) e l’altezza (\(X\), in cm) di \(n\) persone. I dati sono rappresentati nel grafico seguente.
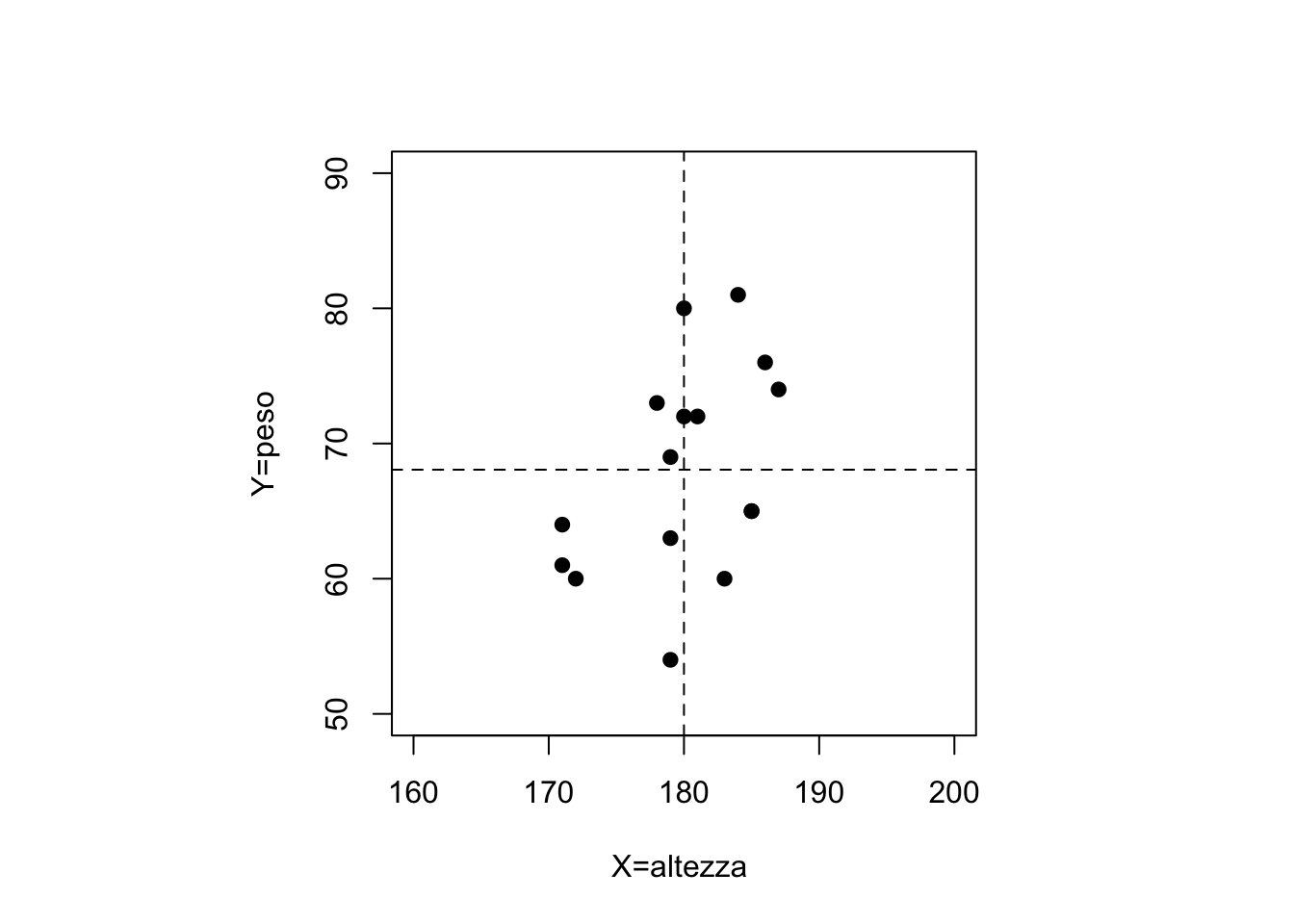
Nel grafico, sono rappresentate anche le medie campionarie delle due variabili, ovvero i valori \[ \bar{x}=\frac{\sum_{i=1}^nx_i}{n}=\frac{x_1+x_2+\ldots+x_n}{n}, \quad \bar{y}=\frac{\sum_{i=1}^n y_i}{n}=\frac{y_1+y_2+\ldots+y_n}{n}. \] Lo scopo del modello lineare è ipotizzare un relazione lineare del tipo \[ Y=mX+q, \] per opportuni valori reali del coefficiente angolare \(m\) e dell’intercetta \(q\). Lo scopo di questa relazione è predire, in corrispondenza dell’osservazione \(x_i\), il valore della variabile \(y_i\).
Sui dati osservati, il valore predetto dal modello di lineare in corrispondenza della osservazione \(x_i\) è dato da \[ \hat{y}_i=mx_i+q. \] In generale, esso si discosterà dall’effettivo valore osservato di \(y_i\), producendo quindi un errore. Lo scopo del modello lineare è trovare la relazione lineare (quindi i valori di \(q,m \in \mathbb{R}\)) che produca il minimo errore possibile.
Nella pratica, l’errore globalmente commesso dalla retta di regressione viene misurato sommando gli scarti quadratici tra i valori osservati \(y_i\) della variabile dipendente e i valori predetti \(\hat{y}_i\) prodotti dalla retta di regressione. Il modello di regressione cerca quindi di trovare \[\begin{equation} \min \sum_{i=1}^n\left(y_i-\hat{y}_i\right)^2 =\min_{(q,m) \in \mathbb{R}^2} \sum_{i=1}^n\, (y_i-mx_i-q)^2. \tag{9.4} \end{equation}\] Dato che si cerca di minimizzare una somma di quadrati, il modello di regressione lineare è anche detto metodo dei minimi quadrati. Si osservi che la funzione obiettivo del modello di regressione \(f(q,m)=\sum_{i=1}^n\, (y_i-mx_i-q)^2\) è una funzione delle due variabili \(q,m\) libere di variare su tutto \(\mathbb{R}^2\), mentre i valori \(x_i,y_i, 1 \leq i \leq n,\) sono delle costanti.
Il problema di regressione è dunque un problema di ottimizzazione non vincolata di tipo A, per cui un eventuale punto di minimo è da ricercarsi tra i punti stazionari della funzione obiettivo.
Si cercano quindi eventuali punti stazionari della funzione obiettivo calcolando le sue derivate parziali e uguagliandole a zero, quindi risolvendo il sistema: \[ \begin{cases} \frac{\partial f}{\partial q}=-2\sum_{i=1}^n(y_i-mx_i-q)=0, \\ \frac{\partial f}{\partial m}=-2\sum_{i=1}^n(y_i-mx_i-q)x_i=0. \end{cases} \] Dividendo per \(-2\) la prima equazione del sistema, e sostituendo le medie campionarie prima definite, si ricava che \[ \sum_{i=1}^n y_i-m\sum_{i=1}^nx_i-nq=n\bar{y}-mn\bar{x}-nq=0 \quad \Rightarrow \quad \bar{y}-m\bar{x}-q=0, \] ovvero \[\begin{equation} \boldsymbol{\bar{y}=m\bar{x}+q}. \tag{9.5} \end{equation}\] Questa equazione esprime il fatto che la retta di regressione lineare dovrà passare per il punto \((\bar{x},\bar{y})\) determinato dalle medie campionarie delle due variabili.
Analogamente, dividendo per \(-2\) la seconda equazione del sistema, si ricava \[ \sum_{i=1}^n x_iy_i-m\sum_{i=1}^nx_i^2-q\sum_{i=1}^nx_i=\sum_{i=1}^n x_iy_i-m\sum_{i=1}^nx_i^2-qn\bar{x}=0. \] Sostituendo nell’ultima equazione la relazione \(q=\bar{y}-m\bar{x}\) precedentemente trovata, si ottiene \[ \sum_{i=1}^n x_iy_i-m\sum_{i=1}^nx_i^2-(\bar{y}-m\bar{x})n\bar{x}=\sum_{i=1}^n x_iy_i-m\sum_{i=1}^nx_i^2-n\bar{x}\bar{y}+mn\bar{x}^2=0, \] da cui si arriva a \[ \left(\sum_{i=1}^n x_iy_i-n\bar{x}\bar{y}\right)=m\left(\sum_{i=1}^nx_i^2-n\bar{x}^2\right). \] Se \(\sum_{i=1}^nx_i^2-n\bar{x}^2 \neq 0\) (questo succede se le \(n>1\) osservazioni \((x_i,y_i)\) non sono già tutte allineate su una retta), si ottiene \[\begin{equation} \boldsymbol{m=\frac{\left(\sum_{i=1}^n x_iy_i-n\bar{x}\bar{y}\right)}{\left(\sum_{i=1}^nx_i^2-n\bar{x}^2\right)}}. \tag{9.6} \end{equation}\] Le due equazioni (9.6) e (9.5) determinano l’unico punto stazionario della funzione \(f(q,m)\).
Per capirne la natura, si calcola la matrice Hessiana \[ H_f(q,m)=\left(\begin{array}{cc} 2n & 2n \bar{x} \\ 2n \bar{x} & 2\sum_{i=1}^n x_i^2\end{array}\right)=2n\left(\begin{array}{cc} 1 & \bar{x} \\ \bar{x} & \left(\sum_{i=1}^n x_i^2\right)/n\end{array}\right). \] Controllando quindi le condizioni del Teorema 9.3, si ha che \(\frac{\partial^2 f}{\partial x^2}=1>0\) e \[ \text{det}\, (H_f(q,m)) =\frac{\sum_{i=1}^n x_i^2}{n}-\bar{x}^2>0. \] L’ultima diseguaglianza segue da un noto risultato statistico, nell’ipotesi che le \(x_i\) non siano tutte identiche.
Risulta quindi che il punto stazionario trovato, e determinato dalle equazioni (9.6) e (9.5), è un punto di minimo assoluto per \(f(q,m)\) e rappresenta i parametri della retta di regressione ottimale.
#Dati riguardanti peso e altezza di n persone
h=c(186,181,171,178,172,179,179,180,187,179,185,171,184,180,185,183)
w=c(76,72,64,73,60,54,69,80,74,63,65,61,81,72,65,60)
#Grafico delle osservazioni
mh=min(h,160)
Mh=max(h,200)
mw=min(w,50)
Mw=max(w,90)
par(mfrow=c(1,1), pty="s")
plot(h,w,xlab="altezza",ylab="peso",pch=19,xlim=c(mh,Mh),ylim=c(mw,Mw))
#Nel grafico vengono riportati i valori medi delle osservazioni
abline(v=mean(h),lty =2,lwd = 1)
abline(h=mean(w),lty =2,lwd = 1)
#calcolo modello di regressione lineare
reg=lm(w~h)
#retta di regressione
abline(reg)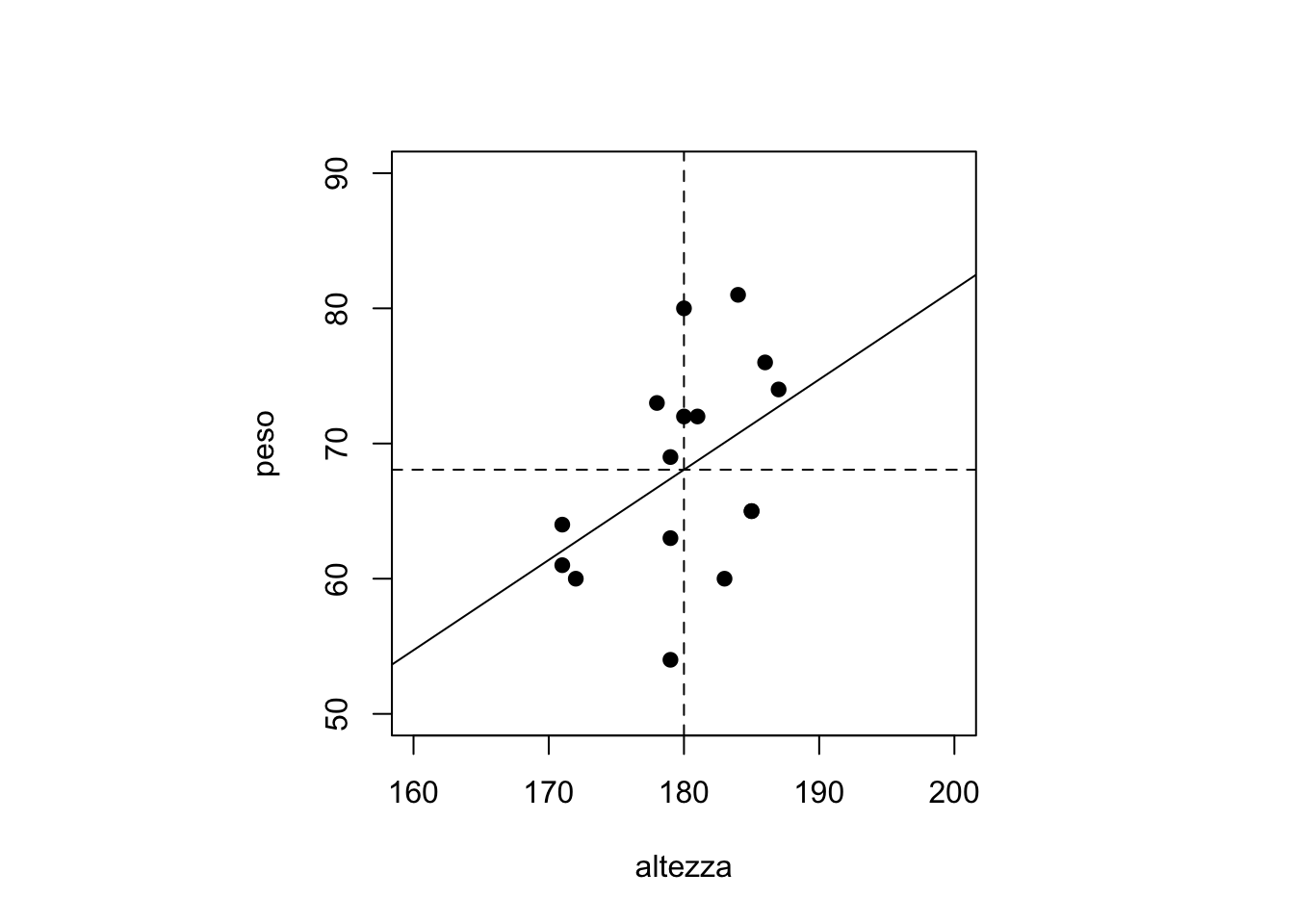
## (Intercept) h
## -52.0897843 0.6675127È possibile sfruttare il calcolo matriciale introdotto nel Capitolo 8 per scrivere in modo molto più elegante e conciso il modello di regressione.
Si definiscano le matrici \[ \mathbf{X}=\left(\begin{array}{cc}1 & x_1 \\1 & x_2 \\ \vdots & 0 \\1 & x_n\end{array}\right), \quad \mathbf{Y}=\left(\begin{array}{c}y_1 \\y_2 \\ \vdots \\ y_n\end{array}\right), \quad \mathbf{b}=\left(\begin{array}{c}q \\m\end{array}\right). \] Si osservi che \(\mathbf{X}\) è una matrice \(n \times 2\), mentre \(\mathbf{Y}\) e \(\mathbf{b}\) sono vettori colonna di dimensioni \(n \times 1\) e, rispettivamente, \(2 \times 1\).
Osservando che \[ \mathbf{Y}^t\mathbf{Y}=\left(\begin{array}{cccc}y_1 & y_2 & \cdots & y_n \end{array}\right)\left(\begin{array}{c}y_1 \\y_2 \\ \vdots \\ y_n\end{array}\right)=y_1^2+y_2^2+\ldots+y_n^2, \] e \[ \mathbf{X}\mathbf{b}= \left(\begin{array}{c}q+mx_1 \\q+mx_2 \\ \vdots \\ q +mx_n\end{array}\right), \] la funzione obiettivo in (9.4) può essere scritta come \[ (\mathbf{Y}-\mathbf{X}\mathbf{b})^t (\mathbf{Y}-\mathbf{X}\mathbf{b}). \] Svolgendo la funzione obiettivo, si trova \[\begin{align*} (\mathbf{Y}-\mathbf{X}\mathbf{b})^t (\mathbf{Y}-\mathbf{X}\mathbf{b})&=\mathbf{Y}^t\mathbf{Y}-(\mathbf{X}\mathbf{b})^t\mathbf{Y}-\mathbf{Y}^t(\mathbf{X}\mathbf{b})+(\mathbf{X}\mathbf{b})^t(\mathbf{X}\mathbf{b})\\&=\mathbf{Y}^t\mathbf{Y}-2(\mathbf{X}\mathbf{b})^t\mathbf{Y}+(\mathbf{X}\mathbf{b})^t(\mathbf{X}\mathbf{b}). \end{align*}\] Il problema (9.4) può essere quindi scritto come
\[ \min_{\mathbf{b} \in \mathbb{R}^2} \quad \mathbf{Y}^t\mathbf{Y}-2(\mathbf{X}\mathbf{b})^t\mathbf{Y}+(\mathbf{X}\mathbf{b})^t(\mathbf{X}\mathbf{b}). \] Il sistema dal quale ricavare i punti stazionari può essere scritto in forma matriciale come \[ \frac{\partial}{\partial \mathbf{b}}\left(\mathbf{Y}^t\mathbf{Y}-2(\mathbf{X}\mathbf{b})^t\mathbf{Y}+(\mathbf{X}\mathbf{b})^t(\mathbf{X}\mathbf{b})\right) =-2\mathbf{X}^t\mathbf{Y}+2\mathbf{X}^t\mathbf{X}\mathbf{b}=0, \] ovvero \[ (\mathbf{X}^t\mathbf{X})\mathbf{b}=\mathbf{X}^t\mathbf{Y}. \] Questo è un sistema lineare che, nel caso \(\mathbf{X}^t\mathbf{X}\) sia invertibile, ha come unica soluzione \[ \mathbf{b}=(\mathbf{X}^t\mathbf{X})^{-1}\mathbf{X}^t\mathbf{Y}. \] Si può verificare che questa scrittura è equivalente alle equazioni (9.6) e (9.5) precedentemente trovate.
9.11 Esercizi
Exercise 9.1 Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione \[f(x,y)=2x^3-4xy+2y, \quad \text{sull'insieme} \quad \{0\leq x \leq 1, 0\leq y \leq 1\}.\]
Exercise 9.2
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione \[f(x,y)=-x^2+2y^3-xy+x-1, \quad \text{sull'insieme} \quad \{0\leq x \leq 1, 0\leq y \leq 1\}.\]Exercise 9.3
Si determinino e classifichino i punti stazionari della funzione \[ f(x,y)=x^3-y^2+6y-12x+5, \] dimostrando per ognuno di essi se si tratta di punti di sella, o punti di massimo/minimo relativi/assoluti.Exercise 9.4
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione \[f(x,y)=-x^2+y^3-y+x-1, \quad \text{sull'insieme} \quad \{0\leq x \leq 1, 0\leq y \leq 1\}.\]Exercise 9.5
Si dica se esistono e nel caso si trovino massimo/minimo assoluti della funzione \[f(x,y)=4x^2+y^2-3x+1, \quad \text{sull'insieme}\quad \{x^2+y^2=1\},\] nel caso indicando dove essi sono eventualmente raggiunti.Exercise 9.6
Classificare la natura di tutti i punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[ f(x,y)=x^2y-2y^2x-3xy+4,\] indicando se essi sono punti di massimo/minimo relativi/assoluti oppure punti di sella.Exercise 9.7
Si dica se esistono e nel caso si determinino massimo/minimo assoluti della funzione \[f(x,y)=2x^2+y^2-1, \quad \text{ sull'insieme }\quad \{x-y^2=3 \},\] nel caso indicando dove essi sono eventualmente raggiunti.Exercise 9.8
Indicare la natura degli eventuali punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R}\), \[f(x,y)=e^{x^2-4xy+y^3},\] indicando se essi sono punti di massimo/minimo relativi/assoluti oppure punti di sella.Exercise 9.9
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione \[f(x,y)=3x^2-y^2+2\quad \text{ sull'insieme }\quad x-y^2=0.\]Exercise 9.10
Si determinino e classifichino i punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[ f(x,y)=x^3-2xy+y^2, \] dimostrando per ognuno di essi se si tratta di punti di sella, o punti di massimo/minimo relativi/assoluti.Exercise 9.11
Trovare e classificare i punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[f(x,y)=2x^4+3x^2+4y^2-y,\] dimostrando per ognuno di essi se si tratta di punti di sella, o punti di massimo/minimo relativi/assoluti.Exercise 9.12
Classificare la natura di tutti i punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[ f(x,y)= -y^2x+2x^2y-xy,\] dimostrando per ognuno di essi se si tratta di punti di sella, o punti di massimo/minimo relativi/assoluti.Exercise 9.13
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione \[f(x,y)=-x^2+2y^3-y+x-1, \quad \text{sull'insieme} \quad \{0\leq x \leq 1, 0\leq y \leq 1\}.\]Exercise 9.14
Si dica se esistono e nel caso si determinino massimo/minimo assoluti della funzione \[f(x,y)=3x+4y, \quad \text{ sull'insieme }\quad \{x^2+y^2=225 \},\] nel caso indicando dove essi sono eventualmente raggiunti.Exercise 9.15
Classificare la natura di tutti i punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[f(x,y)=x^2-2y^2-xy-x^3,\] dimostrando per ognuno di essi se si tratta di punti di sella, o punti di massimo/minimo relativi/assoluti.Exercise 9.16
Classificare la natura di tutti i punti stazionari della funzione \(f:\mathbb{R}^2 \to \mathbb{R},\) \[f(x,y)=(x^2-3xy)e^y,\] dimostrando per ognuno di essi se si tratta di punti di sella, o punti di massimo/minimo relativi/assoluti.Exercise 9.17
Si dica se esistono, e nel caso si trovino i punti di massimo/minimo assoluti della funzione \(f:\mathbb{R}^2 \to \mathbb{R}\), \[ f(x,y)=x^2+y^2+y-1,\quad \text{ sull'insieme }\quad A=\{x^2+y^2 \leq 1\}. \]