1 Preliminari

In questo capitolo introdurremo tutti gli strumenti matematici necessari per affrontare quanto seguirà. In particolare, il programma di questo corso di Matematica si basa su due concetti chiave: la definizione di insieme e quella di funzione. Iniziamo dunque con l’introdurre alcuni elementi di Teoria degli insiemi.

1.1 Teoria degli insiemi

Per gli scopi di questo corso ci è sufficiente dare la seguente definizione triviale di insieme.

Definition 1.1 Un insieme è una collezione di elementi distinti per cui è possibile stabilire univocamente se un dato elemento vi appartiene o meno.

Remark. La definizione di insieme data non è formalmente corretta, in quanto usa il concetto di “collezione” che è di fatto un sinonimo di “insieme”. Gli elementi che vengono dati di seguito fanno parte quindi della cosiddetta teoria “ingenua” o “intuitiva” degli insiemi. È possibile trattare la teoria degli insiemi con un approccio assiomatico, che però oltrepassa gli obiettivi di questo testo. Chi fosse interessato può partire dal cosiddetto Paradosso di Russell.

Indicheremo un insieme con una lettera maiuscola, utilizzando invece lettere minuscole per i suoi elementi. Un insieme può essere definito:

elencando esplicitamente tutti i suoi elementi tra parentesi graffe: \[ A=\{1,2,3\}; \] quando è possibile fare questo, diremo che l’insieme è finito;
indicando la proprietà che devono soddisfare gli elementi che appartengono all’insieme: \[ A=\{n: n \text{ è un numero naturale minore o uguale a 3} \}. \]

Si scrive \(a \in A\) per indicare che l’elemento \(a\) appartiene all’insieme \(A\); ad esempio: \(3 \in A\). In alternativa, scriveremo che \(b \notin A\) per indicare che l’elemento \(b\) non appartiene all’insieme \(A\); ad esempio: \(4 \notin A\).

Siano date le seguenti definizioni:

Si dice insieme vuoto l’insieme \(\emptyset=\{\; \}\) che non contiene alcun elemento.
Si dice che \(B\) è un sottoinsieme di \(A\), e si scrive \(B \subseteq A\), se ogni elemento di \(B\) è anche elemento di \(A\). Formalmente, \(B \subseteq A\) se, per ogni \(b \in B\), si ha \(b \in A\).
Si dice che due insiemi \(A\) e \(B\) sono uguali, e si scrive \(A=B\), se gli elementi di \(A\) sono tutti e soli quelli di \(B\), ovvero se vale sia \(B \subseteq A\) che \(A \subseteq B\).

Alcuni avranno usato in passato i simboli \(\subset\) e \(\subsetneq\) per indicare sottoinsiemi cosiddetti impropri o propri. In quanto segue, e in generale, non ci si avvale di queste notazioni ma si utilizza solamente il simbolo \(\subseteq\) per indicare che un insieme è contenuto in un altro (in un contesto insiemistico si può anche dire che un insieme è più piccolo di un altro).

Dato un insieme \(A\) si dice insieme delle parti di \(A\) l’insieme \(2^A\) che ha come elementi tutti e soli i possibili sottoinsiemi di \(A\).

Remark. Se un insieme \(A\) ha \(n\) elementi, il suo insieme delle parti \(2^A\) possiede \(2^n\) elementi (e questo ne giustifica la notazione). Infatti, per creare un sottoinsieme di \(A\), per ognuno dei suoi \(n\) elementi si hanno due possibilità: includerlo o non includerlo nel sottoinsieme. In totale, si hanno quindi \(2^n\) possibili sottoinsiemi. Ad esempio, se \(A=\{a,b,c\}\), si avranno gli \(2^3=8\) sottoinsiemi \[ 2^A=\left\{\emptyset,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\} \right\}. \] Si osserva dalla notazione usata come l’insieme delle parti sia un insieme di insiemi.

Le principali operazioni insiemistiche che useremo nel seguito sono:

L’unione di due insiemi \(A\) e \(B\), che si indica con \(A \cup B\), è l’insieme formato da tutti gli elementi che appartengono all’insieme \(A\) o all’insieme \(B\) o ad entrambi. Formalmente, \[ A \cup B = \{x: x \in A \text{ o } x \in B\}. \] 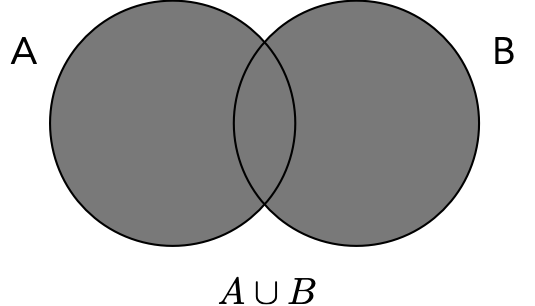Si osservi che ognuno dei due insiemi è più piccolo della loro unione: \[A \subseteq A \cup B,\quad B \subseteq A \cup B.\] Le possibili relazioni tra insiemi possono essere rappresentate tramite i diagrammi di Eulero-Venn, dove le aree in grigio rappresentano l’insieme risultante dalle operazioni insiemistiche indicate.
L’intersezione di due insiemi \(A\) e \(B\), che si indica con \(A \cap B\), è l’insieme formato da tutti gli elementi che appartengono sia all’insieme \(A\) che all’insieme \(B\). Formalmente, \[ A \cap B = \{x: x \in A \text{ e } x \in B\}. \] Se due insiemi \(A\) e \(B\) non hanno elementi in comune, ovvero se la loro intersezione è uguale all’insieme vuoto, \(A \cap B=\emptyset\), si dice che essi sono disgiunti. Si osservi che l’intersezione di due insiemi è più piccola di entrambi: \[A \cap B \subseteq A,\quad A \cap B \subseteq B.\]
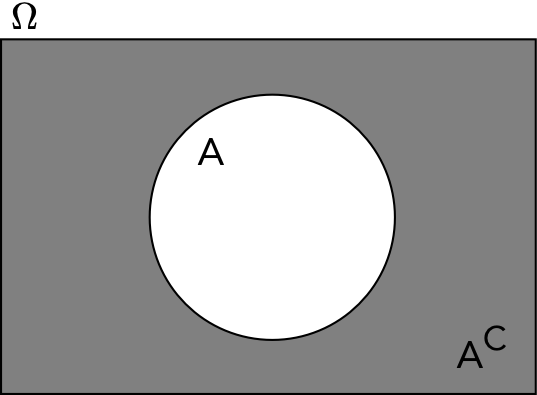
La differenza tra l’insieme \(A\) e l’insieme \(B\), che si indica con \(A \setminus B\), è l’insieme formato da tutti gli elementi che appartengono all’insieme \(A\) ma non all’insieme \(B\). Formalmente, \[ A \setminus B = \{x: x \in A \text{ e } x \notin B\}. \] La differenza tra un insieme di riferimento, detto insieme universo \(\Omega\), e un insieme \(A\) è detta insieme complementare di \(A\) e si indica con \(A^C=\Omega \setminus A\), ovvero \[ A^C = \{x \in \Omega : x \notin A\}. \]

Si osservi il differente uso delle preposizioni “e” ed “o” nel linguaggio comune e nel linguaggio matematico. La risposta alla domanda “Quale è l’insieme dei numeri pari e dispari?” è l’insieme vuoto. La preposizione “e” corrisponde all’intersezione insiemistica, la “o” all’unione. Quale è l’insieme dei numeri pari o dispari?

Utilizzando i diagrammi di Eulero-Venn, si possono facilmente ricavare le seguenti relazioni insiemistiche per insiemi \(A,B,C\) qualunque:

\(A \cup B = B \cup A\) (Commutatività di \(\cup\));
\((A \cup B) \cup C = A \cup (B \cup C)\) (Associatività di \(\cup\));
\(A \cap B = B \cap A\) (Commutatività di \(\cap\));
\((A \cap B) \cap C = A \cap (B \cap C)\) (Associatività di \(\cap\));
\(A \cup (B\cap C) = (A \cup B) \cap (A \cup C)\) (Distributività di \(\cup\) rispetto a \(\cap\));
\(A \cap (B\cup C) = (A \cap B) \cup (A \cap C)\) (Distributività di \(\cap\) rispetto a \(\cup\));
\(A \setminus B = A \cap B^C\);
\((A \cup B)^C= A^C \cap B^C\) (De Morgan, I);
\((A \cap B)^C= A^C \cup B^C\) (De Morgan, II).

1.2 Il concetto di funzione

Una funzione è una relazione tra due insiemi che associa ad ogni elemento di un primo insieme (detto dominio) uno ed un solo elemento di un secondo insieme (detto codominio).

Questa definizione, analogamente a quella di insieme, non è ben posta in quanto usa il concetto di relazione (o corrispondenza, o legge), che altro non è che un sinonimo di quello di funzione.

Se una definizione assiomatica di insieme va oltre gli obiettivi di questo corso, è invece possibile definire rigorosamente il concetto di funzione introducendo il prodotto cartesiano di due insiemi.

Definition 1.2 Il prodotto cartesiano di due insiemi non vuoti \(A\) e \(B\) è l’insieme \(A \times B\) di tutte le possibili coppie ordinate formate da un elemento di \(A\) e uno di \(B\), ovvero: \[ A \times B=\left\{(a,b): a \in A, b \in B\right\}. \]

Dati due insiemi \(A\) e \(B\), possiamo rappresentare un elemento \((a,b)\) del prodotto cartesiano come una freccia che associa l’elemento \(a\) a \(b\). Se invece di considerare tutti gli elementi del prodotto cartesiano (figura seguente in alto), se ne considera solo un sottoinsieme che soddisfa determinate proprietà (figura seguente in basso), si crea una particolare corrispondenza tra gli elementi dei due insiemi che prende il nome di funzione. ::: {.definition} Dati due insiemi non vuoti \(A\) e \(B\), si dice funzione di dominio \(A\) e codominio \(B\), e si indica con \(f:A \to B\), un qualsiasi sottoinsieme \(F \subseteq A \times B\) che contenga per ogni \(a \in A\) una ed una sola coppia \((a,b) \in F\). Se \((a,b) \in F\), si dice che \(f(a)=b\) è l’immagine di \(a\) tramite \(f\). Si dice (insieme) immagine di \(f\) l’insieme \[ \text{Im}(f)=f(A)=\{b \in B : \text{ esiste un elemento } a \in A \text{ tale che } f(a)=b\}. \] :::

La definizione appena data formalizza in modo rigoroso l’idea di funzione come una legge che associa ad ogni elemento del dominio uno ed un solo elemento del codominio. Se usiamo la rappresentazione di una funzione tramite frecce, questo significa che da tutti gli elementi del dominio \(A\) deve partire una ed una sola freccia. Possiamo pensare come esempio alla funzione altezza \(h:A\to \mathbb{N}\) che associa ad ogni studente \(x\) della classe di Matematica \(A\) la sua altezza in centimetri \(h(x) \in \mathbb{N}\). Ogni studente ha una ed una sola altezza: quindi \(h\) è una funzione ben definita.

È semplice individuare perché le seguenti corrispondenze non sono funzioni:

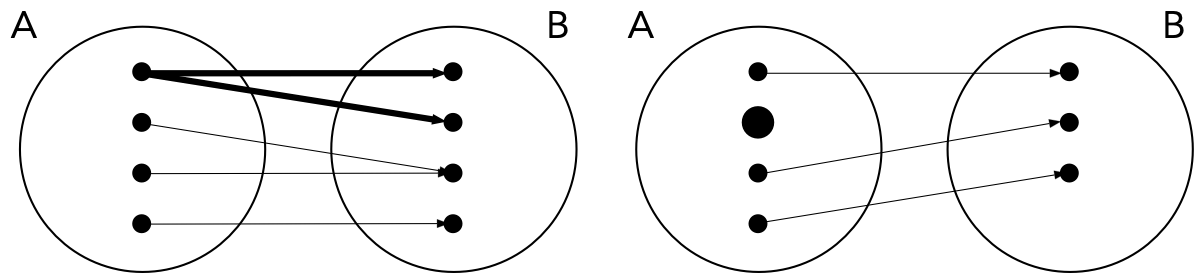
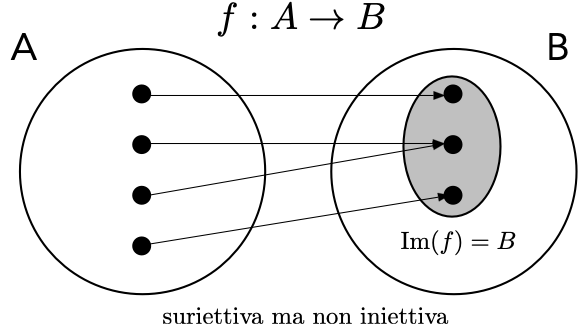
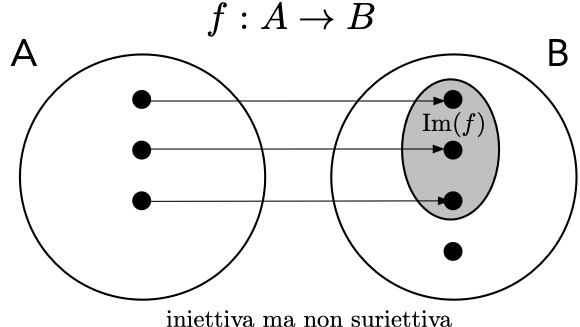
Se ogni elemento del dominio deve avere una immagine tramite una funzione data, non è necessario che tutti gli elementi del codominio siano immagini di un elemento del dominio (nel caso di \(h\) potrebbe non esserci nessuno studente alto 210 cm). Quando il codominio è invece tutto coperto si parla di funzione suriettiva.

Se un elemento del dominio non può avere due immagini differenti, è però possibile che due elementi possano avere la stessa immagine (studenti differenti \(x_1\neq x_2\) potrebbero avere la stessa altezza \(h(x_1)=h(x_2)\)). Quando ciò non accade, si parla di funzione iniettiva.

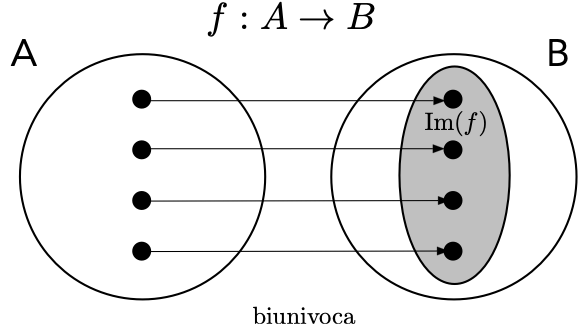
Definition 1.3 Una funzione \(f:A \to B\) si dice:

suriettiva se \(\text{Im}(f)=B\);

iniettiva se \(f(a_1)=f(a_2) \Rightarrow a_1=a_2,\) per ogni \(a_1,a_2 \in A\);
biunivoca (o biettiva) se è sia suriettiva che iniettiva.

Si osservi che si può equivalentemente definire una funzione iniettiva richiedendo che \(a_1 \neq a_2 \Rightarrow f(a_1)\neq f(a_2),\) per ogni \(a_1,a_2 \in A\).

1.3 Gli insiemi numerici

“1, 2, 3, 4, 5, 6, 7,… Cosa potrebbe essere più semplice di così? Eppure sono stati i numeri, forse più di ogni altra cosa, a permettere all’umanità di trascinarsi fuori dal fango e di puntare alle stelle.”

(Cit. dal primo capitolo di Numeri incredibili di Ian Stewart, Ed. Bollati Boringhieri)

Tutti sappiamo contare, tutti usiamo dei numeri e tutti sappiamo indicare un numero preciso di oggetti. Ma che cos’è un numero? In particolare, che cosa è un numero naturale?

Si consideri l’insieme \(\mathcal{H}\) avente come elementi tutti i possibili insiemi finiti, ovvero tutti quelli per cui è possibile elencare esplicitamente tutti gli elementi. \(\mathcal{H}\) è un insieme difficile da immaginare: appartengono ad esso l’insieme degli studenti che sta seguendo questo corso, l’insieme dei caratteri usati in questo libro, etc… Se volessimo fare ordine in questa immensa collezione di insiemi, potremmo ad esempio classificare ogni insieme appartenente ad \(\mathcal{H}\) sulla base del numero di elementi posseduti. In una immaginaria e infinita cassettiera, potremmo mettere in ogni cassetto tutti gli insiemi aventi lo stesso numero di elementi. Ma come facciamo a contare gli elementi degli insiemi se non abbiamo a disposizione i numeri?

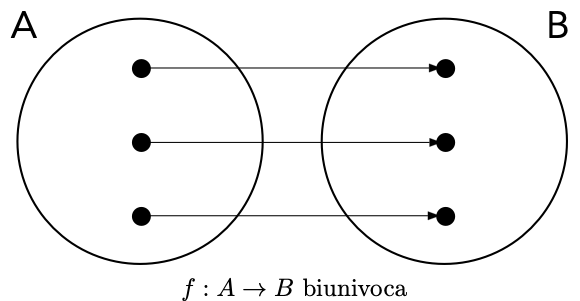
La necessità di usare i numeri è nata probabilmente proprio dall’esigenza di contare, ovvero di stabilire se due insiemi dati hanno lo stesso numero di elementi. A pensarci bene, però, per contare non servono necessariamente i numeri: quello che facciamo quando stabiliamo che due insiemi hanno lo stesso numero di elementi è usare il concetto di funzione biunivoca.

È evidente come una funzione biunivoca corrisponda alla nostra intuitiva nozione di insiemi aventi lo stesso numero di elementi.

Definition 1.4 Si dice che due insiemi \(A\) e \(B\) hanno la stessa cardinalità, e si scrive che \(\#A=\#B\) se esiste una qualsiasi funzione \(f:A \to B\) che sia biunivoca.

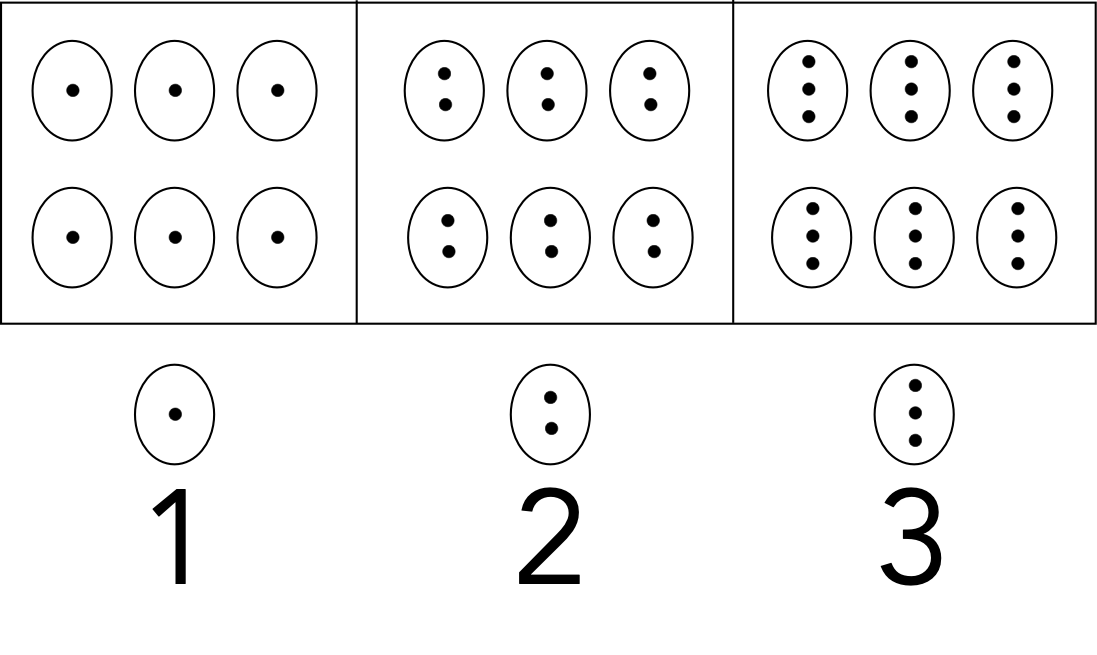
Sulla base di questo principio, possiamo quindi creare dei sottoinsiemi di \(\mathcal{H}\), che chiamiamo classi (i nostri cassetti nell’esempio immaginario), ognuna contenente insiemi aventi la stessa cardinalità. Dal punto di vista insiemistico, tutti gli elementi di ognuna di queste classi sono indistinguibili, ovvero hanno la stessa proprietà. Basterebbe uno di loro, il cosiddetto rappresentante della classe, per descriverli tutti. Potremmo quindi scegliere un insieme qualsiasi da ogni cassetto e metterlo come etichetta del cassetto stesso. Questa etichetta è quello che noi chiamiamo numero, e a cui ogni cultura ha associato un simbolo e un nome.

Definition 1.5 Un numero è l’insieme rappresentante di tutti gli insiemi che sono in corrispondenza biunivoca tra loro e con esso, e che solitamente indichiamo con un simbolo: \(1,2,3,\ldots.\) All’insieme vuoto viene associato il numero \(0\).

L’insieme dei numeri naturali è indicato (comprendendo o meno lo \(0\)) come \[ \mathbb{N}=\{1,2,3, \ldots\}, \quad \mathbb{N}_0=\{0,1,2,3, \ldots\}. \]

Dall’insieme dei numeri naturali discendono tutti gli altri insiemi numerici:

l’insieme dei numeri interi \(\mathbb{Z}\) che corrispondono all’insieme ottenuto unendo i numeri naturali, lo 0, e i numeri interi negativi, cioè quelli ottenuti ponendo un segno \(-\) davanti ai naturali: \[ \mathbb{Z}=\{\ldots,-3,-2,-1,0,1,2,3,\ldots\}; \]
l’insieme dei numeri razionali \(\mathbb{Q}\) che corrispondono alle frazioni \(m/n\) aventi un numero intero al numeratore e un numero intero non nullo al denominatore: \[ \mathbb{Q}=\left\{x=\frac{m}{n}: m,n \in \mathbb{Z}, n \neq 0 \right\}. \]

Un numero (razionale) può essere scritto in notazione decimale (ovvero espresso come somma di potenze di \(10\)), come ad esempio \[ 320,13=\frac{32013}{100}= 3 \times 10^2 + 2 \times 10^1 + 0\times 10^0 +1\times 10^{-1}+3\times 10^{-2}. \] I numeri decimali che possono essere scritti utilizzando solo un numero finito di posizioni decimali si dicono numeri decimali limitati, come ad esempio \[ \frac{1}{2}=0,5; \] altrimenti, numeri decimali illimitati, come ad esempio \[ \frac{1}{3}=0,33333\ldots=0,\overline{3}. \] I numeri razionali hanno la particolarità di possedere una rappresentazione decimale periodica, ovvero dopo una certa posizione decimale continuano a ripetere la stessa sequenza finita di cifre (eventualmente tutti 0), come ad esempio

\[\begin{align*} \frac{1}{2}=0,5=0,50000\ldots&=0,5\overline{0},\\ \frac{1}{7}=0,142857142857142857\ldots&=0,\overline{142857}. \end{align*}\]

Si possono scrivere però numeri decimali illimitati che non ripetono mai la stessa sequenza di cifre, ad esempio quello che comunemente viene indicato come “pi greco”: \[ \pi=3,14159265358979323846264338327950288419716939937510\ldots \simeq 3,14. \]

La ricerca del più grande numero possibile di cifre decimali di \(\pi\) ha caratterizzato la storia della Matematica. Se oggi è possibile calcolare \(\pi\) con migliaia di miliardi di cifre decimali, è da considerarsi notevole l’impresa del matematico cinese Zu Chongzhi, vissuto nel V secolo, che calcolò sei cifre decimali di \(\pi\) tramite l’elegante approssimazione con \(\frac{355}{113}\). Passò quasi un millennio prima che si riuscisse ad ottenere una approssimazione migliore.

I numeri decimali illimitati e non periodici, come \(\pi, \sqrt{2}, \log{3}\), sono detti numeri irrazionali.

L’insieme dei numeri reali \(\mathbb{R}\) è l’unione dell’insieme dei numeri razionali (numeri decimali con rappresentazione periodica) e dell’insieme dei numeri irrazionali (numeri decimali con rappresentazione non periodica). \(\mathbb{R}\) comprende quindi qualsiasi numero decimale illimitato.

Si osservi che \[ \mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R}, \] e che lo stesso numero può avere rappresentazioni differenti: \[ 1= \frac{2}{2}=1,\overline{0}=0,\overline{9}. \] Fissata una unità di misura, è possibile rappresentare un numero reale \(x \in \mathbb{R}\) su una linea, detta la retta (reale). Ogni punto sulla retta rappresenta quindi un numero.

1.4 Intervalli e sistema ampliato dei numeri reali

Nel seguito diremo che un numero reale \(x \in \mathbb{R}\) è:

positivo se \(x>0\);
negativo se \(x<0\);
non negativo se \(x \geq 0\);
non positivo se \(x \leq 0\).

Se alla retta reale aggiungiamo i due punti \(+\infty\) e \(-\infty\) otteniamo l’insieme \(\mathbb{R}^*\) che viene chiamato il sistema ampliato dei numeri reali, ovvero \[ \mathbb{R}^*=\mathbb{R} \cup \{+\infty,-\infty\}. \] L’elemento \(+\infty\) ha la proprietà di essere più grande di qualsiasi numero reale, \(+\infty > x, \; x \in \mathbb{R}\), mentre \(-\infty\) di essere più piccolo di qualsiasi numero reale, \(-\infty < x, \; x \in \mathbb{R}\).

Anche su \(\mathbb{R}^*\) possiamo definire le comuni operazioni di somma, differenza, prodotto e quoziente, tenendo conto delle seguenti regole, per \(x \in \mathbb{R}\):

\(+\infty+x =+\infty, \; -\infty+x =-\infty\);
\(+\infty+(+\infty) =+\infty, \; -\infty+(-\infty) =-\infty\);
\(+\infty-(-\infty) =+\infty, \; -\infty-(+\infty) =-\infty\);
\(x(+\infty) =+\infty,\quad x(-\infty) =-\infty,\quad \text{se } x>0\);
\(x(+\infty) =-\infty,\quad x(-\infty) =+\infty,\quad \text{se } x<0\);
\(+\infty(+\infty)=+\infty;\;-\infty(-\infty)=+\infty;\;+\infty(-\infty)=-\infty;\;-\infty(+\infty)=-\infty\);
\(\frac{x}{\pm \infty}=0\);
\(\frac{+\infty}{x}=+\infty,\; \frac{-\infty}{x}=-\infty\quad \text{se } x>0\);
\(\frac{+\infty}{x}=-\infty,\; \frac{-\infty}{x}=+\infty\quad \text{se } x<0\).

Non tutte le operazioni sono possibili sul sistema ampliato dei numeri reali. Rimangono indeterminate le forme \(+\infty+(-\infty), -\infty+(+\infty)\), \(0\,(\pm\infty), (\pm \infty)\,0\), \(\frac{\pm \infty}{\pm \infty}\), \(\frac{0}{0}\).

Dati due numeri reali \(a,b \in \mathbb{R}\), con \(a<b\), sono definiti i seguenti insiemi, detti intervalli:

\([a,b]=\{ x \in \mathbb{R}: a \leq x \leq b \}\);
\((a,b)=\{ x \in \mathbb{R}: a < x < b \}\);
\([a,b)=\{ x \in \mathbb{R}: a \leq x < b \}\);
\((a,b]=\{ x \in \mathbb{R}: a < x \leq b \}\);
\([a,+\infty)=\{ x \in \mathbb{R}: x \geq a \}\);
\((a,+\infty)=\{ x \in \mathbb{R}: x > a \}\);
\((-\infty,b]=\{ x \in \mathbb{R}: x \leq b \}\);
\((-\infty,b)=\{ x \in \mathbb{R}: x < b \}\);
\((-\infty,+\infty)=\mathbb{R}\).

Alcune particolari tipologie di intervalli, dette intorni, assumeranno un particolare rilievo in quanto segue.

Definition 1.6 Si dice intorno del punto \(x\) (di raggio \(r>0\)) l’insieme di tutti i punti che distano da \(x\) meno di \(r\), ovvero l’intervallo \[ I_r(x)=(x-r,x+r). \] In particolare si dicono intorno sinistro e intorno destro di \(x\) (di raggio \(r>0\)) gli intervalli \[ I_r^-(x)=(x-r,x) \quad \text{ e } \quad I_r^+(x)=(x, x+r). \] Per \(M \in \mathbb{R}\), si dice intorno di \(+\infty\), risp. \(-\infty\), qualsiasi intervallo del tipo \[ (M,+\infty), \text{ risp. } (-\infty,M). \]

Si osservi che l’unione dell’intorno sinistro di un numero con quello destro non risulta essere pari all’intorno completo (manca proprio \(x\)): \[ I_r^-(x) \cup I_r^+(x) =I_r(x) \setminus \{x\}. \]

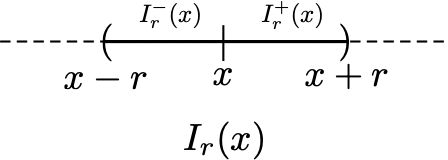
Nel seguito, si potrà indicare un intorno del punto \(x\) anche semplicemente con \(I(x)\), omettendo l’indicazione del raggio quando questa non sia rilevante.

Sulla definizione di intorno si basano le seguenti semplici nozioni topologiche, che introduciamo sulla retta reale e studieremo, in particolare, sui suoi intervalli.

Definition 1.7 Un punto \(x \in A \subseteq \mathbb{R}\) si dice interno all’insieme \(A\) se esiste un suo intorno \(I_r(x)\) contenuto in \(A\), \(I_r(x) \subseteq A\). Un insieme \(A\subseteq \mathbb{R}\) si dice aperto se tutti i suoi punti sono interni ad esso.

È immediato verificare che un intervallo del tipo \((a,b)\) è aperto: è sempre possibile racchiudere ogni suo punto in un intorno sufficientemente piccolo da essere contenuto nell’intervallo.

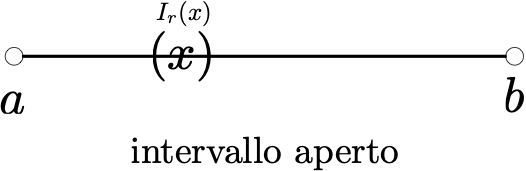
Definition 1.8 Un insieme \(A \subseteq \mathbb{R}\) si dice chiuso se il suo complementare \(A^C\) è aperto.

È immediato verificare che un intervallo del tipo \([a,b]\) è chiuso: risulta infatti che il suo complementare \((-\infty,a) \cup (b,+\infty)\) è aperto.

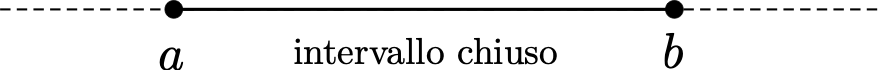
Attenzione al fatto che un insieme che non è aperto non è necessariamente chiuso, ovvero esistono insiemi che non sono né aperti né chiusi. Si prenda ad esempio l’intervallo \((a,b]\): esso non è aperto in quanto non è possibile trovare un intorno di \(x=b\) in esso totalmente contenuto (qualsiasi punto a destra di \(b\) non appartiene all’intervallo). Analogamente, non è nemmeno chiuso perché lo stesso ragionamento rimane valido per il punto \(x=a\) del suo complementare \((-\infty,a] \cup (b,+\infty)\). Analogamente, l’intervallo \([a,b)\) non è né aperto né chiuso.

È possibile quindi stabilire che:

\((a,b)\) è aperto (tutti i suoi punti sono interni);
\([a,b]\) è chiuso (il suo complementare è aperto);
\([a,b)\) e \((a,b]\) non sono né aperti né chiusi;
\((-\infty,b)\) e \((a,+\infty)\) sono aperti (tutti i loro punti sono interni);
\((-\infty,b]\) e \([a,+\infty)\) sono chiusi (i loro complementari sono del tipo precedente quindi aperti);
\((-\infty,+\infty)=\mathbb{R}\) è aperto (tutti i suoi punti sono interni).

Negli intervalli, quindi, sono gli estremi a fare la differenza tra l’essere un insieme aperto o chiuso o né aperto né chiuso. Gli estremi di fatto delimitano il confine dell’intervallo.

Definition 1.9 Un punto \(x \in \mathbb{R}\) (non necessariamente in \(A\)) si dice di frontiera per l’insieme \(A \subseteq \mathbb{R}\) se tutti i suoi intorni \(I_r(x)\), \(r>0\), contengono un punto di \(A\) e uno di \(A^C\).

Una ultima definizione sarà fondamentale per la definizione di limite nel Capitolo 3.

Definition 1.10 Un punto \(x \in \mathbb{R}^*\) si dice di accumulazione per l’insieme \(A \subseteq \mathbb{R}\) se tutti i suoi intorni \(I_r(x)\), \(r>0\), contengono un punto di \(A\) diverso da \(x\).

È possibile dimostrare che un insieme è chiuso se e solo se contiene tutti i suoi punti di accumulazione, come infatti avviene per gli intervalli del tipo \([a,b]\).

1.5 Estremi di un insieme

Se si considera l’intervallo \([a,b]\) è intuitivamente immediato riferirsi al punto \(a\) come al suo minimo (l’elemento più piccolo), al punto \(b\) come al suo massimo (l’elemento più grande).

Definition 1.11 Dato un insieme \(A \subseteq \mathbb{R}\), \(M\) si dice massimo di \(A\) se

\(M \geq a, \text{ per ogni } a \in A\);
\(M \in A\).

\(m\) si dice minimo di \(A\) se

\(m \leq a, \text{ per ogni } a \in A\);
\(m \in A\).

Il massimo (minimo) è il più grande (piccolo) elemento di un insieme. Si osservi come la definizione data imponga non solo che l’elemento massimo (minimo) sia più grande (piccolo) di tutti gli elementi dell’insieme ma anche che esso stesso appartenga all’insieme.

Un insieme costituito da un numero finito di elementi possiede sempre massimo e minimo.

Se un insieme è invece costituito da un numero infinito di elementi, minimo e massimo potrebbero non esistere. Si prenda ad esempio in considerazione l’insieme \((a,b)\). Considerando i suoi elementi ci accorgiamo immediatamente che nessuno di essi è più grande di tutti gli altri, né nessuno è più piccolo. Nell’intervallo \((0,1)\), ad esempio, per quanto si scelga un numero grande a piacimento (ad es. \(0,999\)) se ne può sempre trovare uno più grande (ad es. \(0,9999\)); per quanto se ne scelga uno positivo prossimo a 0 (ad es. \(0,001\)), se ne può sempre trovare uno positivo più piccolo (ad es. \(0,0001\)). In casi come questi il massimo (minimo) non esiste. Per ovviare a questo problema, si introducono due concetti che invece esistono sempre, finiti o infiniti: l’estremo inferiore e l’estremo superiore.

Anche se l’intervallo \((a,b)\) non ha né massimo né minimo, è tuttavia vero che i suoi due punti di frontiera \(a\) e \(b\) svolgono un ruolo particolare. Di tutti i numeri che sono più grandi degli elementi dell’insieme (detti maggioranti), \(b\) è infatti il più piccolo. Di tutti i numeri che sono più piccoli degli elementi dell’insieme (detti minoranti), \(a\) è infatti il più grande. In generale, si dà la seguente definizione.

Definition 1.12 Un insieme \(A \subseteq \mathbb{R}\) si dice limitato superiormente se esiste una costante \(K\) tale che \(K \geq a\), per ogni \(a \in A\).

Dato \(A \subseteq \mathbb{R}\) limitato superiormente, si dice estremo superiore di \(A\) il numero \(M=\sup A\) tale che:

\(M \geq a, \text{ per ogni } a \in A\);
fissato a piacimento \(\epsilon >0\), esiste \(a \in A\) tale che \(a>M-\epsilon\).

Se un insieme non è limitato superiormente, allora si pone \(\sup A =+\infty\).

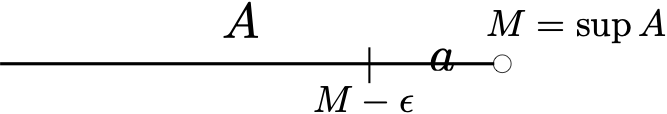
Si osservi che il primo requisito per essere considerato l’estremo superiore di un insieme è identico al primo requisito per essere il massimo: il numero deve essere un maggiorante dell’insieme, ovvero deve essere più grande di tutti gli elementi dell’insieme. La differenza la fa appartenere o meno all’insieme stesso. Di tutti i possibili maggioranti, l’estremo superiore è il più piccolo. Se l’estremo superiore appartiene all’insieme, allora è anche il massimo. Analogamente, si definisce l’estremo inferiore.

Definition 1.13 Un insieme \(A \subseteq \mathbb{R}\) si dice limitato inferiormente se esiste una costante \(k\) tale che \(k \leq a\), per ogni \(a \in A\).

Dato \(A \subseteq \mathbb{R}\) limitato inferiormente, si dice estremo inferiore di \(A\) il numero \(m=\inf A\) tale che:

\(m \leq a, \text{ per ogni } a \in A\);
fissato a piacimento \(\epsilon >0\), esiste \(a \in A\) tale che \(a<m+\epsilon\).

Se un insieme non è limitato inferiormente, allora si pone \(\inf A =-\infty\).

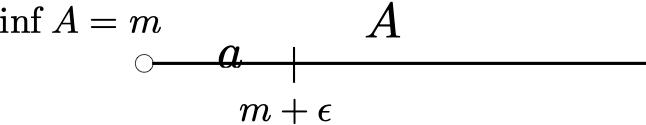
Per gli scopi di questo testo, è sufficiente considerare che in un intervallo di tipo \((a,b)\), i due estremi sono rispettivamente l’estremo inferiore e l’estremo superiore dell’intervallo. Nel caso appartenessero all’intervallo (come in \([a,b]\)), allora assumeranno anche il ruolo di minimo e massimo.

Nel caso di intervalli \((a,+\infty)\) illimitati superiormente, l’estremo inferiore \(a\) è anche il minimo solo se appartiene all’insieme (come nel caso \([a,+\infty)\)); nel caso di intervalli \((-\infty,b)\) illimi-tati inferiormente, l’estremo superiore \(b\) è anche il massimo solo se appartiene all’insieme (come nel caso \((-\infty,b]\)).

1.6 Proprietà delle funzioni reali

L’oggetto di studio dei prossimi capitoli saranno le funzioni del tipo \(f:A \subseteq \mathbb{R} \to \mathbb{R}\), ovvero le funzioni aventi come codominio l’insieme dei numeri reali \(\mathbb{R}\). Parleremo, più brevemente, di funzioni reali.

Una funzione reale \(f:A\subseteq \mathbb{R} \to \mathbb{R}\) viene usualmente visualizzata attraverso il suo grafico, ovvero attraverso l’insieme \[ \mathcal{G}_f=\{(x,f(x)) \in \mathbb{R}\times\mathbb{R}: x \in A\}. \] Così come è possibile rappresentare un numero reale \(x \in \mathbb{R}\) sulla retta reale, è possibile rappresentare coppie ordinate di numeri \((x,y) \in \mathbb{R}\times\mathbb{R}\) su un piano, detto piano cartesiano. Il piano cartesiano viene rappresentato mediante due assi perpendicolari, detti asse delle ascisse (dove viene individuata la \(x\)) e asse delle ordinate (dove viene individuata la \(y\)), che si incontrano in un punto \(\mathcal{O}\) detto origine (degli assi). Il grafico di una funzione può essere quindi disegnato sul piano cartesiano individuando tutte le coppie \((x,f(x))\) per cui la ascissa \(x\) è qualsiasi valore del dominio di \(f\), e la ordinata \(y\) è il corrispondente valore \(y=f(x)\).

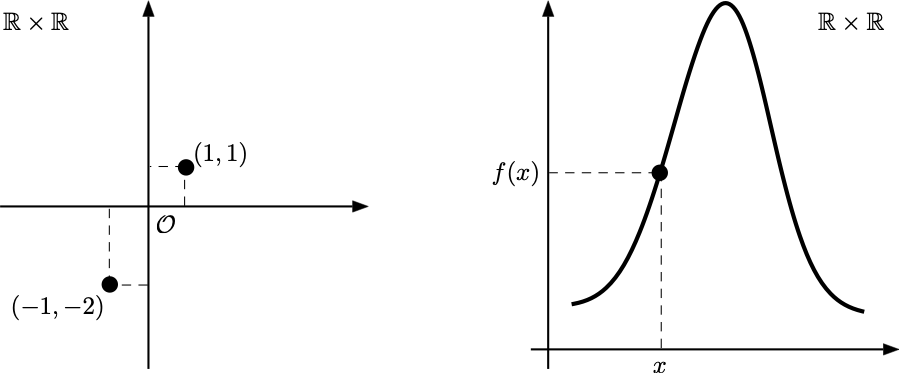
Il grafico di una funzione reale di una variabile reale è un sottoinsieme del prodotto cartesiano \(\mathbb{R} \times \mathbb{R}\) ed è quindi un oggetto bidimensionale.

Seppur oggi il suo utilizzo possa apparire scontato, il Piano Cartesiano fu introdotto (solo) nel 1637 da René Descartes (Cartesio). Nella sua semplicità l’idea di Cartesio fu molto influente in quanto permise la rappresentazione grafica delle espressioni algebriche.

Le principali due proprietà delle funzioni reali che studieremo nel dettaglio sono immediatamente riconoscibili dal loro grafico. Esse sono la monotonia e la convessità.

Il concetto di monotonia racchiude quelli di funzione crescente o funzione decrescente. Questi due concetti sono molto intuitivi e già conosciuti. Le seguenti definizioni li forma-lizzano usando il linguaggio matematico.

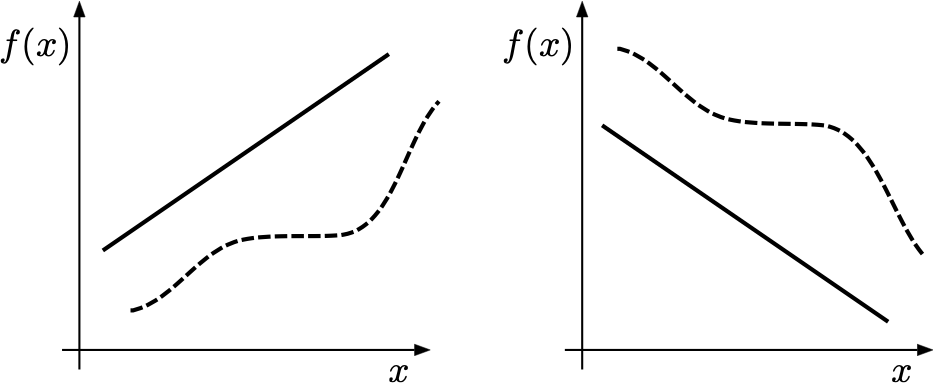
Definition 1.14 Una funzione \(f:A\subseteq \mathbb{R} \to \mathbb{R}\) si dice crescente se, per ogni \(x_1,x_2 \in A\), si ha che \[ x_1 < x_2 \Rightarrow f(x_1) \leq f(x_2). \] Una funzione \(f:A\subseteq \mathbb{R} \to \mathbb{R}\) si dice strettamente crescente se, per ogni \(x_1,x_2 \in A\) si ha che \[ x_1 < x_2 \Rightarrow f(x_1) < f(x_2). \]

Richiedere la stretta monotonia di una funzione significa eliminare la possibilità di avere tratti costanti, come illustrato dalla funzione con il grafico tratteggiato nella figura seguente.

Per definire la decrescenza di una funzione si potrebbero riportare le definizioni date in precedenza con il verso delle corrispondenti diseguaglianze invertito. Più elegantemente, si può dare la seguente definizione.

Definition 1.15 Una funzione \(f:A \subseteq \mathbb{R} \to \mathbb{R}\) si dice (strettamente) decrescente se \(-f\) è (strettamente) crescente, dove \(-f:A \to \mathbb{R}\) è definita come \((-f)(x)=-f(x)\).

Una funzione costante \(f:\mathbb{R} \to \mathbb{R}, f(x)= k\), è sia crescente che decrescente. Non esistono funzioni che siano sia strettamente crescenti che strettamente decrescenti.

La seconda proprietà fondamentale delle funzioni reali è la loro convessità. Una funzione è convessa se il segmento che unisce due punti qualsiasi del suo grafico giace al di sopra del grafico stesso. Questo concetto informale corrisponde alla seguente definizione formale.

Definition 1.16 Una funzione \(f:\mathbb{R} \to \mathbb{R}\) si dice convessa se, per ogni \(x_1,x_2 \in \mathbb{R}\), si ha che \[ \lambda f(x_1) + (1-\lambda) f(x_2) \geq f(\lambda x_1+(1-\lambda)x_2), \; \text{ per ogni } \lambda \in [0,1]. \] 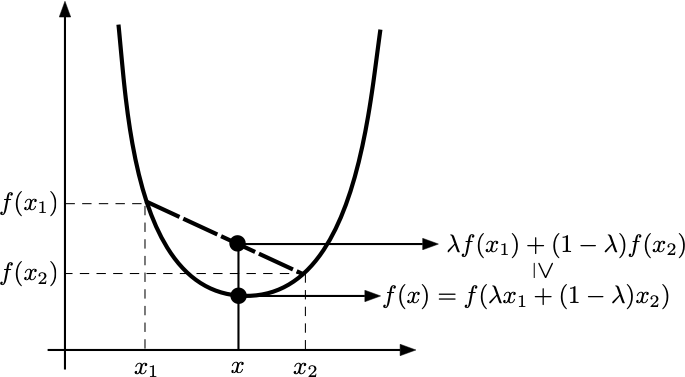La precedente disuguaglianza è sempre soddisfatta con il segno di \(=\) per \(\lambda={0,1},\) o nel caso in cui \(x_1=x_2\). Se questi sono gli unici casi per cui essa vale con il segno di \(=\), si dice che la funzione è strettamente convessa.

Una funzione \(f:\mathbb{R} \to \mathbb{R}\) si dice (strettamente) concava se \(-f\) è (strettamente) convessa.

Richiedere la stretta convessità (concavità) di una funzione significa eliminare la possibilità di avere segmenti nel suo grafico, come illustrato dalla funzione con il grafico tratteggiato nella figura seguente.

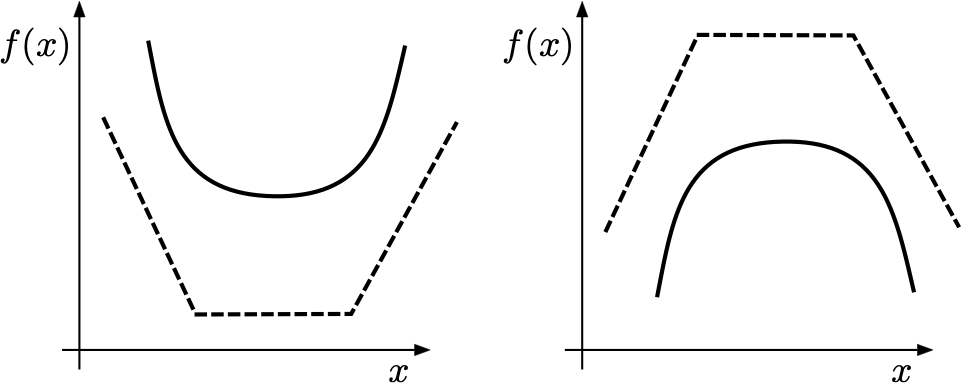
La definizione di convessità può essere data analogamente anche per funzioni aventi come dominio un intervallo \(I \subseteq \mathbb{R}\).

1.7 Esercizi propedeutici al corso

Per affrontare il proseguimento del corso, è necessario saper calcolare le soluzioni delle seguenti disequazioni. Il procedimento per la loro risoluzione verrà illustrato in alcuni esempi nel Capitolo 2.

Exercise 1.1

\(2-\frac{5}{2}x \leq 0\)

Exercise 1.2

\(2x+4 < \frac{2}{3}x+5\)

Exercise 1.3

\(2x^2-3x+4 \leq 0\)

Exercise 1.4

\(-x^2+4x-4 \geq 0\)

Exercise 1.5

\(-2x^2+3x+5 \geq 0\)

Exercise 1.6

\(x- \sqrt{x-2} \leq 0\)

Exercise 1.7

\(2x+\sqrt{x-1} \geq 0\)

Exercise 1.8

\(2 + \sqrt[3]{x-1} \geq 0\)

Exercise 1.9

\(-x + 1 +\sqrt[3]{x^3-3x^2} \leq 0\)

Exercise 1.10

\(x+ \vert x-1\vert \geq 0\)

Exercise 1.11

\(\frac{x}{(x-2)^2}\geq 0\)

Exercise 1.12

\(\frac{1}{x-1}-\frac{1}{x-2}\leq 0\)

Exercise 1.13

\(e^{2x^2-1}<e^{2x-1}\)

Exercise 1.14

\(\frac{x^2-2x}{1-x}\geq 0\)

Exercise 1.15

\(3x-\vert 1-x \vert \leq 0\)

Exercise 1.16

\(e^{x^2-2x-3}\geq 1\)

Exercise 1.17

\(\log(x-1)\leq 2\)

Exercise 1.18

\(\log(x^3)\geq 0\)

Exercise 1.19

\(\log(-x^2+1)\leq \log(x^2+3)\)

Exercise 1.20

\(\log (x^2-1) \leq 2\)