5 Ottimizzazione univariata

In questo capitolo si utilizzeranno tutti i concetti studiati fino a questo punto per calcolare i massimi e i minimi di una qualsiasi funzione di una variabile e per disegnarne il grafico.

5.1 Massimi e minimi di una funzione

Calcolare il massimo e/o il minimo di una funzione è un processo che prende il nome di ottimizzazione. L’attributo univariata del titolo di questo capitolo si riferisce al fatto che verrà ottimizzata una funzione $f(x)$ di una variabile reale.

Ricordiamo la definizione di massimo/minimo di un insieme data nel Capitolo 1.

Definition 5.1 Dato un insieme $A \subseteq \mathbb{R}$, $M$ si dice massimo di $A$ se

$M \geq a, \text{ per ogni } a \in A$;
$M \in A$.

$m$ si dice minimo di $A$ se

$m \leq a, \text{ per ogni } a \in A$;
$m \in A$.

Il massimo/minimo (assoluto) di una funzione sarà dunque definito come il massimo/minimo dei valori assunti dalla funzione, ovvero il massimo/minimo della sua immagine.

Definition 5.2 Data una funzione $f: A \subseteq \mathbb{R} \to \mathbb{R}$:

si dice massimo (assoluto) di $f$ e si indica con $\max f$ il massimo (se esiste) dell’insieme $\text{Im}(f)$;
si dice minimo (assoluto) di $f$ e si indica con $\min f$ il minimo (se esiste) dell’insieme $\text{Im}(f)$.

Equivalentemente, $M=\max f$ se \[\begin{equation} M=f(x_M) \geq f(x) \text{ per ogni } x \in A, \tag{5.1} \end{equation}\] e il punto $x_M$ è detto punto di massimo (assoluto) per $f$.

Equivalentemente, $m=\min f$ se \[\begin{equation} m=f(x_m) \leq f(x) \text{ per ogni } x \in A, \tag{5.2} \end{equation}\] e il punto $x_m$ è detto punto di minimo (assoluto) per $f$.

Remark. Osserviamo i seguenti punti fondamentali sulla definizione di massimo/minimo:

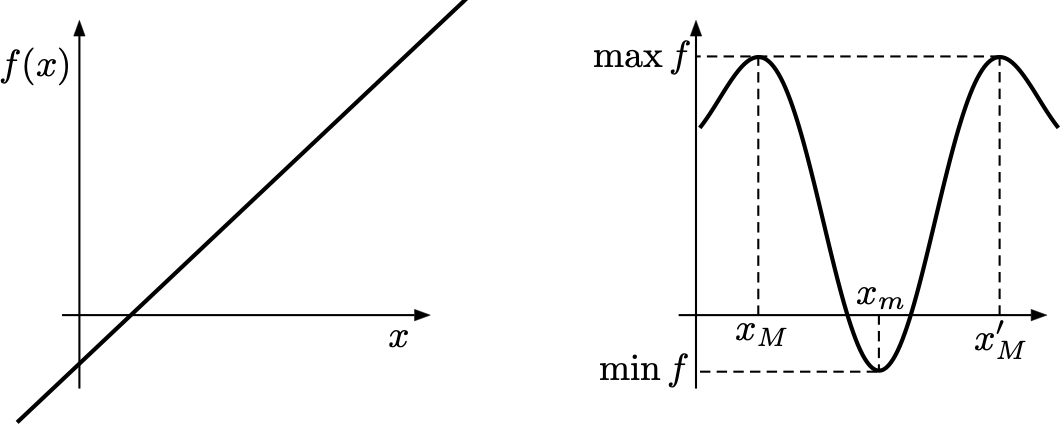
una funzione può non avere minimo o massimo (si veda la figura seguente, a sinistra);
una funzione può avere al più un massimo ed al più un minimo, ma essi possono essere assunti in più punti di massimo/minimo (si veda la figura seguente, a destra);

un punto di massimo/minimo fa parte del dominio di una funzione ed è quindi situato sull’asse delle ascisse in un piano cartesiano;
un massimo/minimo fa parte dell’immagine di una funzione ed è quindi situato sull’asse delle ordinate in un piano cartesiano;
nel caso una funzione non ammetta massimo/minimo, si possono comunque definire i suoi estremi superiore e inferiore come gli estremi superiore e inferiore della sua immagine;
se l’immagine di una funzione non è limitata superiormente, ovvero il suo estremo superiore è $+\infty$, la funzione non ammette massimo; se l’immagine di una funzione non è limitata inferiormente, ovvero il suo estremo inferiore è $-\infty$, la funzione non ammette minimo;
se si parla di (punto di) massimo/minimo di una funzione, senza l’indicazione di un attributo, si intende un (punto di) massimo/minimo assoluto.

Nei grafici delle funzioni di seguito, identificheremo i massimi/minimi assoluti con un circoletto pieno.

5.2 Esistenza di massimo e minimo

Ci sono due domande principali alle quali vogliamo dare risposta in questo capitolo:

Sotto quali condizioni esistono il minimo e il massimo di una funzione?
Dove possono collocarsi i punti di massimo/minimo di una funzione?

Per rispondere al primo quesito, enunciamo il più famoso teorema di esistenza del massimo/minimo di una funzione.

Theorem 5.1 (Teorema di Weierstrass) Una funzione $f:[a,b] \to \mathbb{R}$ continua su un intervallo chiuso e limitato ammette sia massimo che minimo.

La dimostrazione del Teorema di Weierstrass esula dagli scopi di questo testo, ma il suo enunciato è intuitivamente immediato: se si prova a tracciare il grafico di una funzione continua (ovvero senza mai staccare la penna dal foglio) su un intervallo chiuso (che include quindi gli estremi) e limitato, la funzione, a meno di non essere costante (in quel caso avrebbe minimo uguale al massimo), deve forzatamente avere un massimo e un minimo nella sua immagine.

Chiarisce ulteriormente il Teorema di Weierstrass dare alcuni esempi in cui le sue conclusioni non sono raggiunte per mancanza di validità di una delle sue ipotesi.

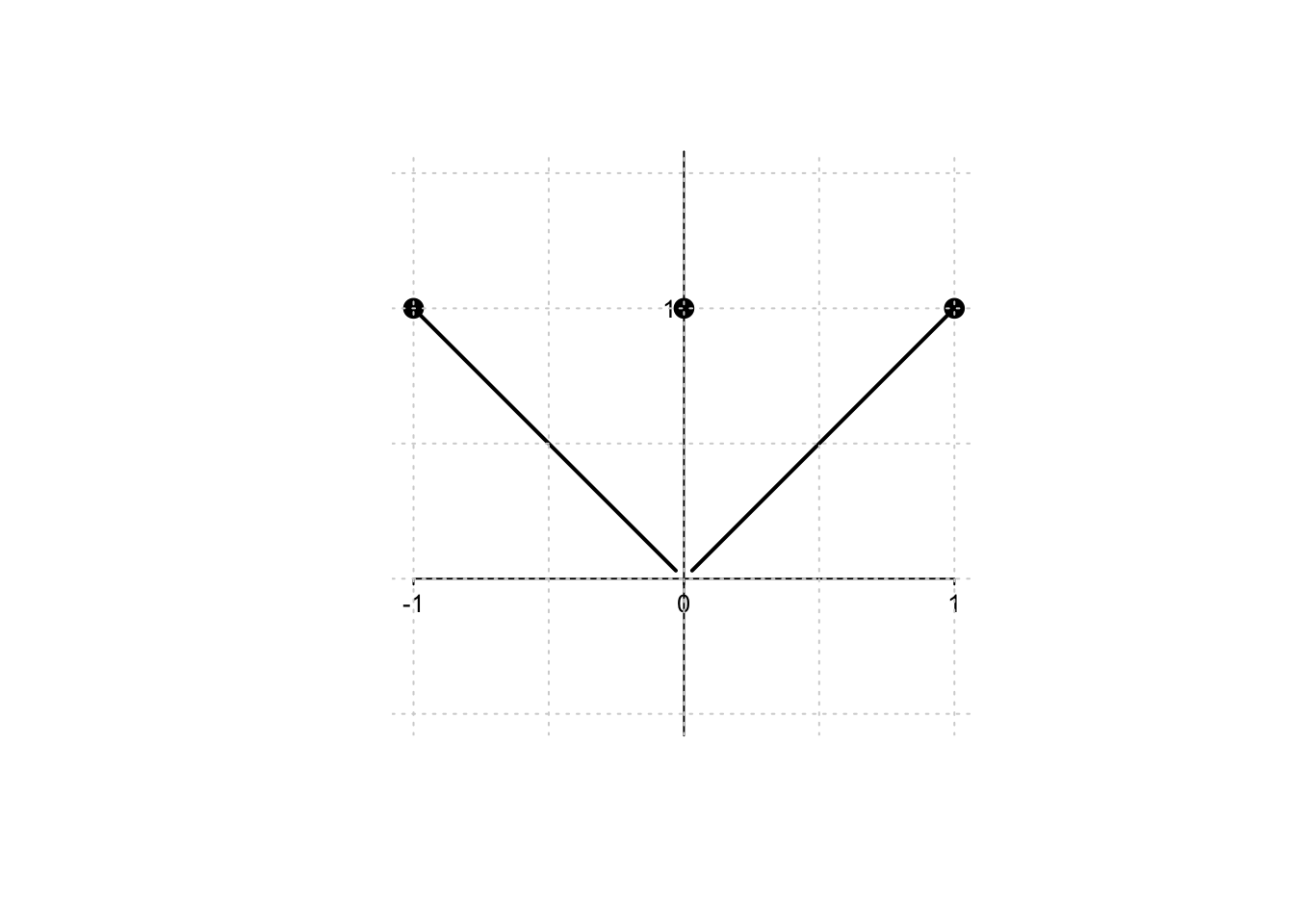
Example 5.1 Si consideri la funzione $f:[-1,1] \to \mathbb{R},$ definita da \[ f(x)=\begin{cases} |x|, &\text{ se } x \neq 0; \\ 1, &\text{ se } x = 0. \end{cases} \] Si può verificare immediatamente dal grafico che la funzione ammette massimo ma non ammette minimo. Infatti, le condizioni del Teorema di Weierstrass non sono rispettate poiché la funzione non è continua nel punto $x=0$. Si osservi che la funzione ha tre punti di massimo.

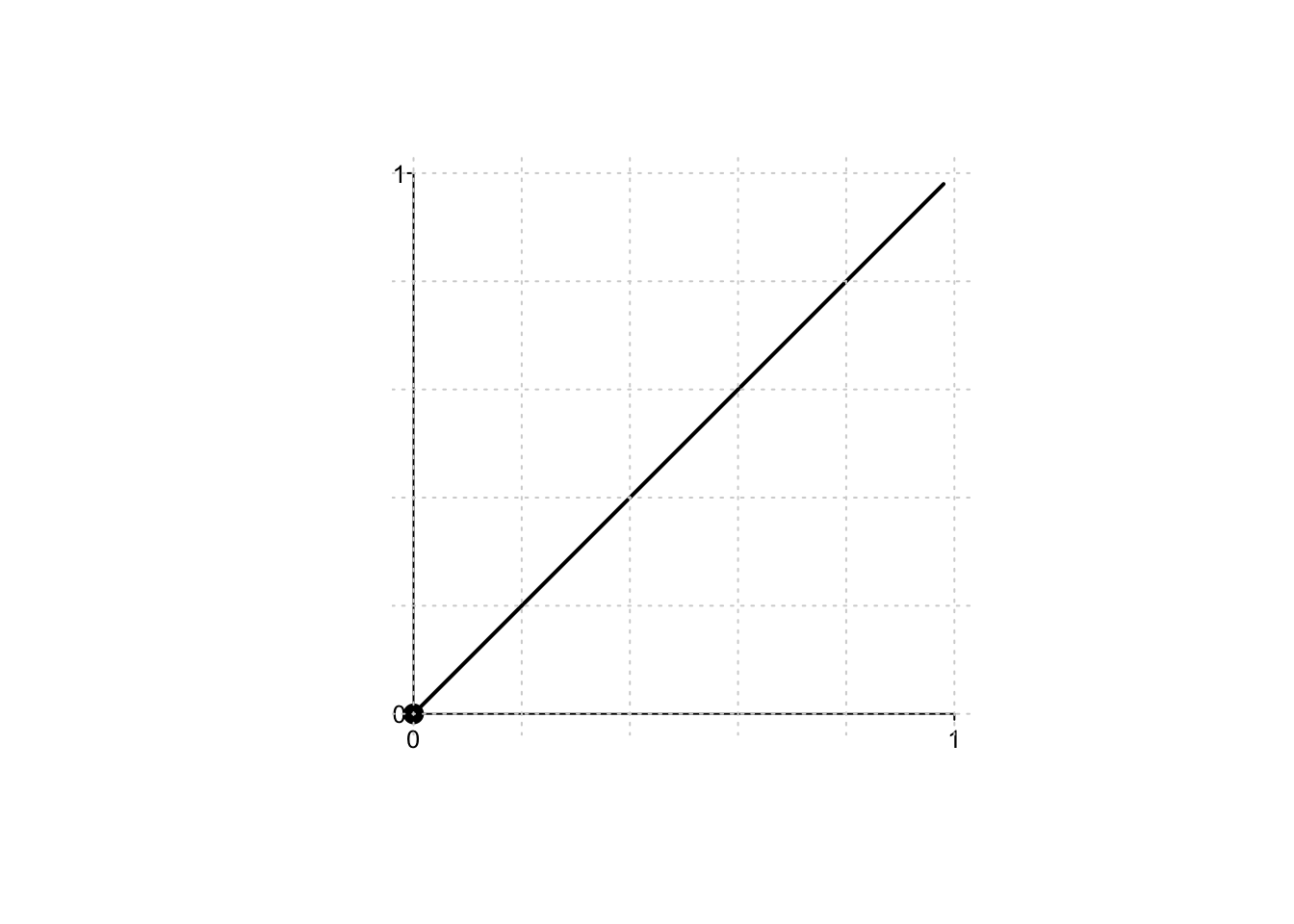
Example 5.2 Si consideri la funzione $f:[0,1) \to \mathbb{R},$ definita da \[ f(x)=x. \] Si può verificare immediatamente dal grafico che la funzione ammette minimo ma non ammette massimo. Infatti, le condizioni del Teorema di Weierstrass non sono rispettate poiché la funzione, pur continua, non è definita su un intervallo chiuso.

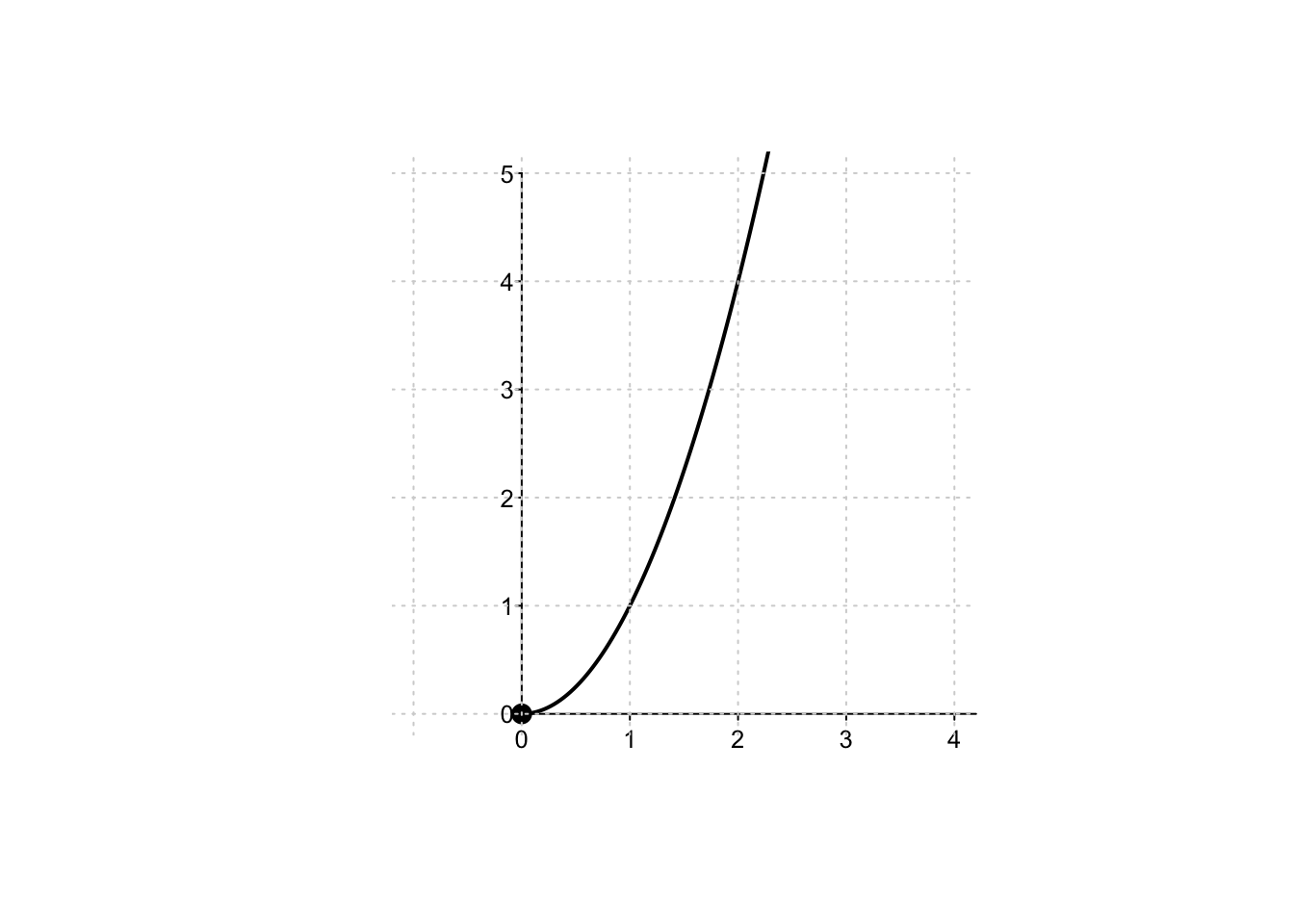
Example 5.3 Si consideri la funzione $f:[0,+\infty) \to \mathbb{R},$ definita da \[ f(x)=x^2. \] Si può verificare immediatamente dal grafico che la funzione ammette minimo ma non ammette massimo. Infatti, le condizioni del Teorema di Weierstrass non sono rispettate poiché la funzione, pur continua, non è definita su un intervallo limitato.

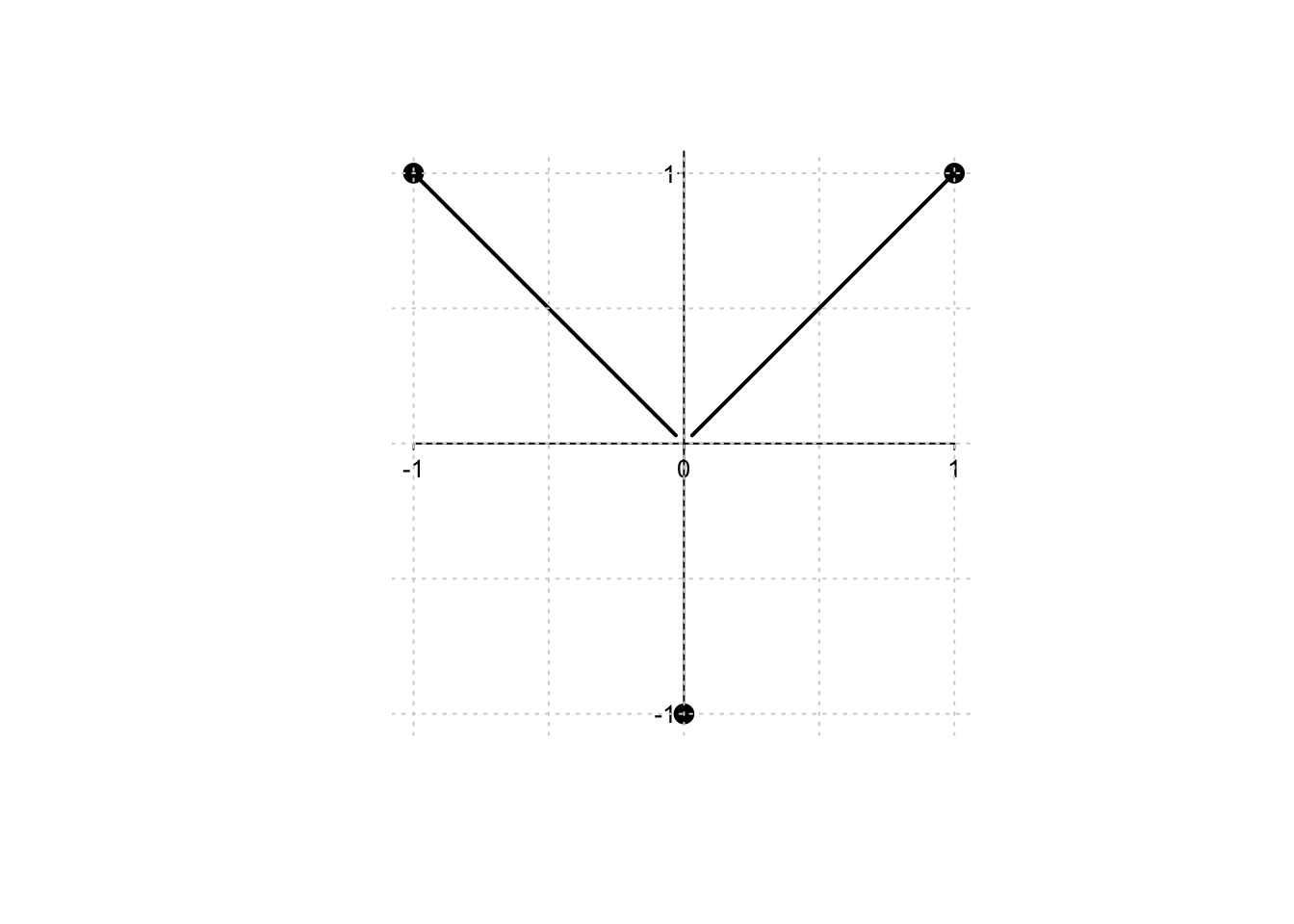
Il Teorema di Weierstrass garantisce l’esistenza di massimo e minimo di una funzione sotto determinate condizioni. Ciò non vuole dire che una funzione non possa avere massimo e minimo anche se non rispetta le ipotesi del teorema. Ad esempio la funzione $f:[-1,1] \to \mathbb{R},$ definita da \[ f(x)=\begin{cases} |x|, &\text{ se } x \neq 0; \\ -1, &\text{ se } x = 0, \end{cases} \] non è continua ma possiede sia massimo che minimo (si veda la figura di seguito).

5.3 Condizione del primo ordine e max/min locali

Una volta stabilito quando una funzione ammette massimo/minimo, è necessario studiare dove possono collocarsi i punti di massimo/minimo all’interno del dominio di una funzione.

In generale, possiamo operare la seguente distinzione. Una funzione può avere punti di massimo/minimo:

nei punti interni al suo dominio;
nei punti di frontiera inclusi nel suo dominio.

I punti di minimo o massimo interni al dominio di una funzione hanno un comportamento distinto e prevedibile. Basti pensare infatti a cosa accade nell’intorno di un punto di massimo di una funzione derivabile con derivata continua. Prima del massimo la funzione è crescente e ha dunque derivata positiva, dopo il massimo è decrescente e ha derivata negativa. Se la derivata varia con continuità, nel punto di massimo essa si annullerà.

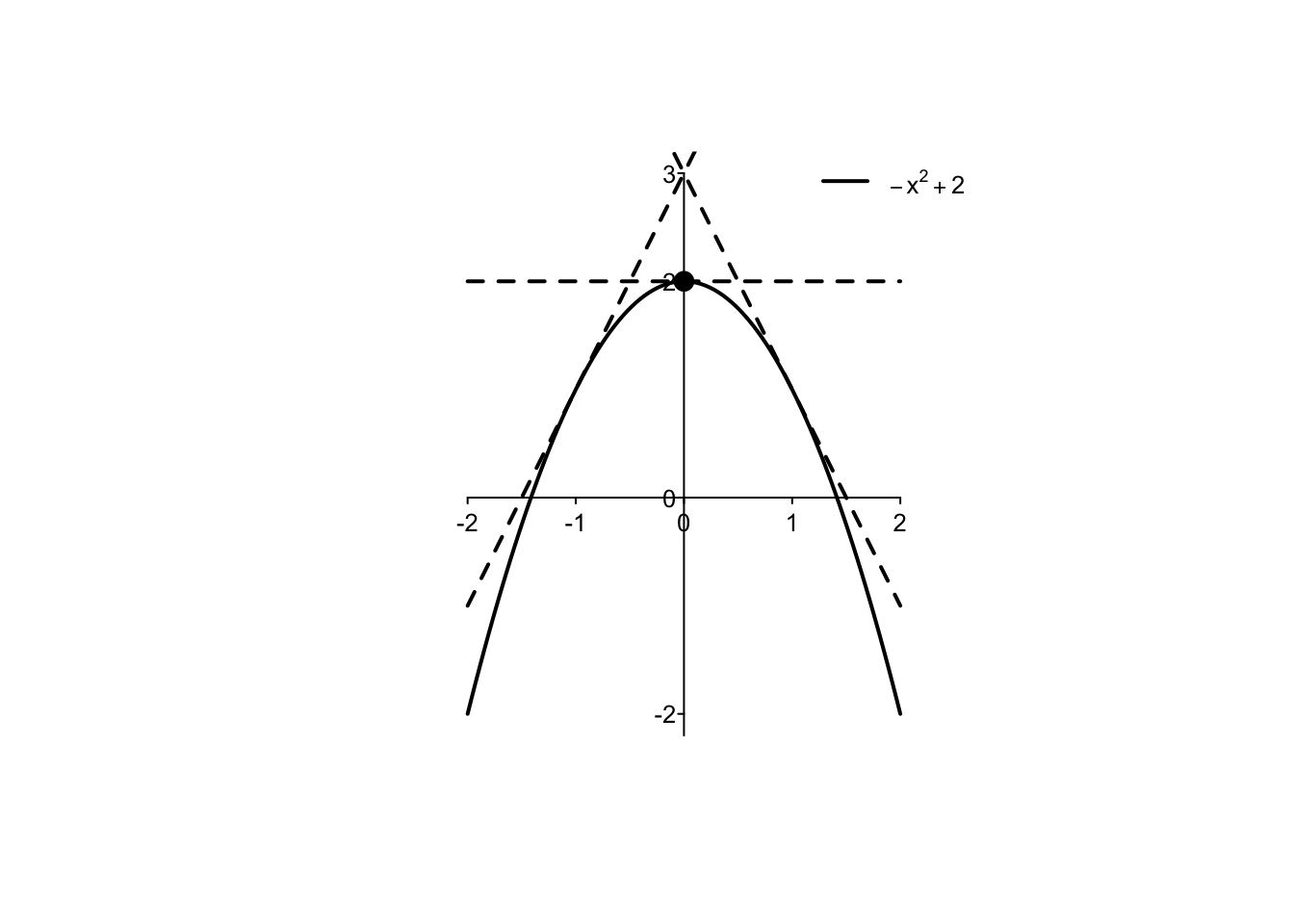
Come esempio, si osservi nel grafico seguente cosa accade nell’intorno del punto di massimo assoluto $x_M=0$ per la funzione $f:\mathbb{R} \to \mathbb{R}, f(x)=-x^2+2$.

Theorem 5.2 (Condizione del primo ordine per punti di massimo/minimo) Data la funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$, sia $x_M \in A$ un suo punto di massimo (o di minimo) assoluto interno al suo dominio. Se $f$ è derivabile in $x_M$, allora \[ f'(x_M)=0. \]

Proof. Supponiamo che $x_M \in A$ sia un punto di massimo assoluto interno al dominio della funzione, e $I(x_M)\subseteq A$ un suo intorno contenuto in $A$. Allora $f(x) \leq f(x_M)$ per ogni $x \in A$ e quindi in particolare per ogni $x \in I(x_M)$. Per $h >0$ con $x_M+h\in I(x_M)$, si ha quindi che $f(x_M+h)-f(x_M) \leq 0$ e quindi \[ \frac{f(x_M+h)-f(x_M)\,(\mathbf{-})}{h \,(\mathbf{+})}\leq 0. \] Essendo $f$ derivabile in $x=x_M$ deve esistere la derivata destra ed essere \[ f'_{+}(x_M)=\lim_{h \to 0^+} \frac{f(x_M+h)-f(x_M)\,(\mathbf{-})}{h \,(\mathbf{+})}\leq 0. \] Per $h <0$ con $x_M-h\in I(x_M)$, si ha invece che \[ \frac{f(x_M+h)-f(x_M)\,(\mathbf{-})}{h \,(\mathbf{-})}\geq 0. \] Essendo $f$ derivabile in $x=x_M$ deve esistere la derivata sinistra ed essere \[ f'_{-}(x_M)=\lim_{h \to 0^-} \frac{f(x_M+h)-f(x_M)\,(\mathbf{-})}{h \,(\mathbf{-})}\geq 0. \] Dato che $f$ è derivabile in $x=x_M$, derivata sinistra e destra devono coincidere con la derivata della funzione, ovvero si deve avere \[ f'(x_M)=f'_{-}(x_M)\geq 0,\quad f'(x_M)=f'_{+}(x_M)\leq 0, \] da cui l’unica possibilità è che \[ f'(x_M)= 0. \] La dimostrazione nel caso di punto di minimo è analoga e lasciata per esercizio.

Un punto $x$ per cui $f'(x)=0$ è detto punto stazionario per la funzione derivabile $f$. La condizione del primo ordine afferma quindi che un punto di massimo/minimo interno al dominio di una funzione derivabile deve essere forzatamente un punto stazionario. L’essere un punto stazionario è una condizione necessaria per essere un punto di massimo/minimo, ma non è sufficiente a garantire che ciò avvenga.

La condizione del primo ordine è in generale soddisfatta anche da altri punti, come:

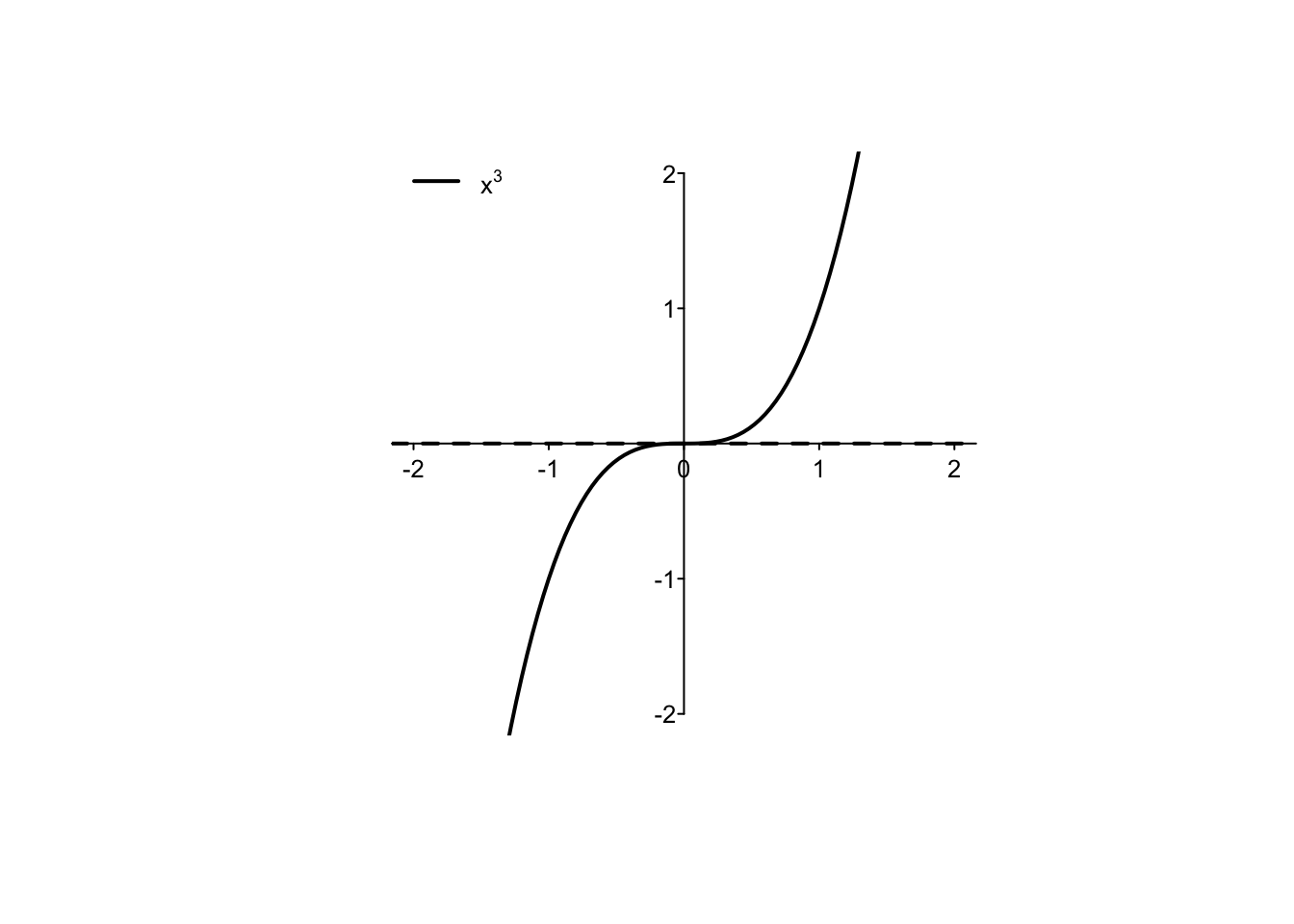
punti in cui la derivata si annulla, ma non cambia di segno. Ad esempio, questo è il caso della funzione cubo $f(x)=x^3$, che possiede derivata $f'(x)=3x^2$ e quindi ha come unico punto stazionario $x=0$. Essendo la funzione strettamente crescente, esso non è né un punto di minimo né un punto di massimo;

punti che sono di massimo/minimo solo localmente, ovvero rispetto ad un intorno sufficientemente piccolo del punto, ma la cui immagine è poi superata (verso l’alto, o verso il basso) in altre regioni del dominio della funzione (si veda il grafico di seguito).

Relativamente a questo ultimo caso, è importante osservare come nella dimostrazione del Teorema 5.2 si utilizzi la proprietà di essere il punto di massimo/minimo di una funzione solo in un intorno sufficientemente piccolo di un punto. Quindi il teorema vale identicamente per quelli che vengono detti punti di massimo/minimo locali (o relativi).

Definition 5.3 Data una funzione $f: A \subseteq \mathbb{R} \to \mathbb{R}$, il punto $x_M$ si dice punto di massimo locale (o relativo) se esiste un suo intorno $I(x_M)$ tale che \[\begin{equation} f(x_M) \geq f(x) \text{ per ogni } x \in I(x_M) \cap A; \tag{5.3} \end{equation}\]

il punto $x_m$ si dice punto di minimo locale (o relativo) se esiste un suo intorno $I(x_m)$ tale che \[\begin{equation} f(x_m) \leq f(x) \text{ per ogni } x \in I(x_m) \cap A. \tag{5.4} \end{equation}\]

È immediato stabilire che un punto di massimo/minimo assoluto ((5.1)-(5.2)) è anche locale ((5.3)-(5.4)), ma non vale il viceversa, come si può vedere dal grafico precedente.

Nei grafici delle funzioni di seguito, identificheremo i punti di massimo/minimo locali ma non assoluti con un circoletto vuoto.

Il Teorema 5.2 vale quindi (con la stessa dimostrazione) per i punti di massimo/minimo locali.

Theorem 5.3 (Condizione del primo ordine per punti di massimo/minimo locali) Data la funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$, sia $x_M \in A$ un suo punto di massimo (o di minimo) locale interno al suo dominio. Se $f$ è derivabile in $x_M$, allora $x_M$ è un punto stazionario, cioè \[ f'(x_M)=0. \]

Come già evidenziato, la condizione del primo ordine non è sufficiente a garantire che un punto stazionario sia in effetti un massimo/minimo, locale o assoluto. Per poter avere questa garanzia, si deve ricavare una informazione supplementare. Un primo modo per farlo è quello di non limitarsi a controllare dove la derivata si annulla, ma studiarne il segno: i punti stazionari in cui la derivata cambia di segno con continuità sono punti di massimo o minimo locali. Per capire se essi sono anche punti di massimo/minimo assoluto, si deve sempre considerare il comportamento della funzione su tutto il suo dominio (trovando tutti i possibili punti di massimo/minimo locali), includendo i punti di frontiera del suo dominio, eventualmente (se possibile) calcolando i limiti per $x \to \pm \infty$.

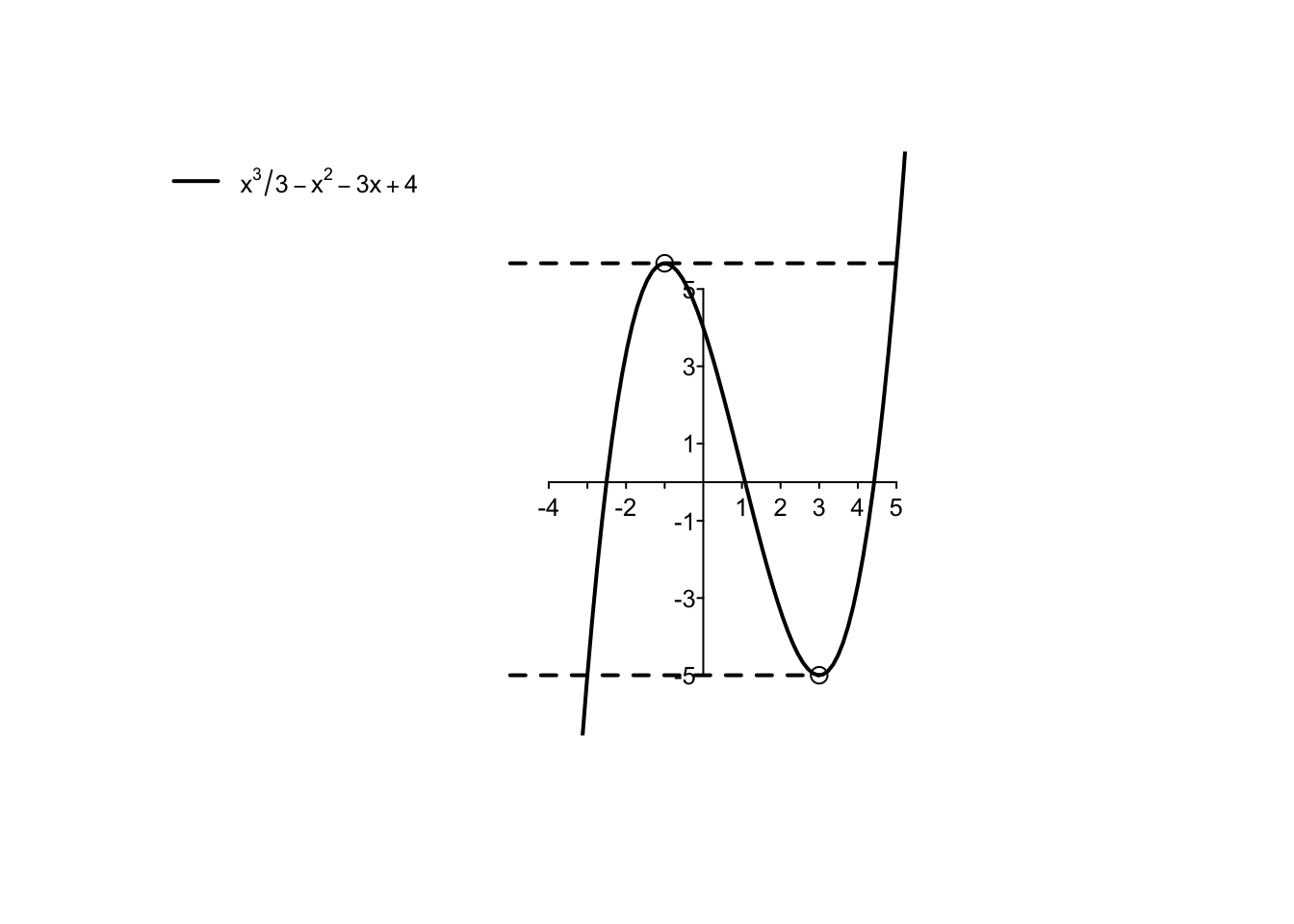
Example 5.4 Si dica se esistono e nel caso si calcolino massimi e minimi assoluti della funzione $f:[-3,6] \to \mathbb{R}$, definita da \[ f(x)=\frac{x^{3}}{3}-x^{2}-3x+4. \] Rispetto all’Esempio 4.16 del Capitolo 4, si osservi che si è ristretto il dominio della funzione all’intervallo $[-3,6]$. Essendo la funzione continua su un intervallo chiuso e limitato, per il Teorema di Weierstrass essa ammette minimo e massimo assoluto. Nel Capitolo 4 avevamo già calcolato, considerando la funzione su tutta la retta reale, che \[ f'(x)=x^2-2x-3 \geq 0 \,\,\, \text{ per } \,\,\, x \in (-\infty,-1]\cup \left[3,+\infty\right). \] Ci sono due punti stazionari nell’intervallo $[-3,6]$:

nel punto $x=-1$ la funzione passa da crescente (derivata positiva) a decrescente (derivata negativa); esso è un punto di massimo relativo dove la funzione assume valore $f(-1)=\frac{17}{3}$;
nel punto $x=3$ la funzione passa da decrescente (derivata negativa) a crescente (derivata positiva); esso è un punto di minimo relativo dove la funzione assume valore $f(3)=-5$.

Per stabilire se i punti stazionari trovati sono anche punti di massimo/minimo assoluto, si deve studiare il comportamento della funzione nei punti non interni compresi nel suo dominio, ovvero agli estremi dell’intervallo $[-3,6]$. Si calcola che $f(-3)=-5$ e $f(6)=22$.

Non possono esserci altri punti in cui la funzione ammette massimo/minimo: all’interno del suo dominio devono essere punti stazionari (e li abbiamo considerati tutti), altrimenti devono essere i punti di frontiera (che abbiamo incluso nella nostra analisi). Confrontando i valori della funzione nei punti trovati, si conclude che:

$\max f=22=f(6)$ raggiunto nel punto di massimo $x_M=6$;
$\min f=-5=f(-3)=f(3)$ raggiunto nei punti di minimo $x_{m_1}=-3$ e $x_{m_2}=3$.

Il punto $x=-1$ è un punto di massimo relativo ma non assoluto.

Il valore della derivata in un punto è il limite del rapporto incrementale della funzione nell’intorno del punto, ed è quindi una informazione locale. Non può essere sufficiente per capire se il punto in questione è un massimo/minimo a livello assoluto.

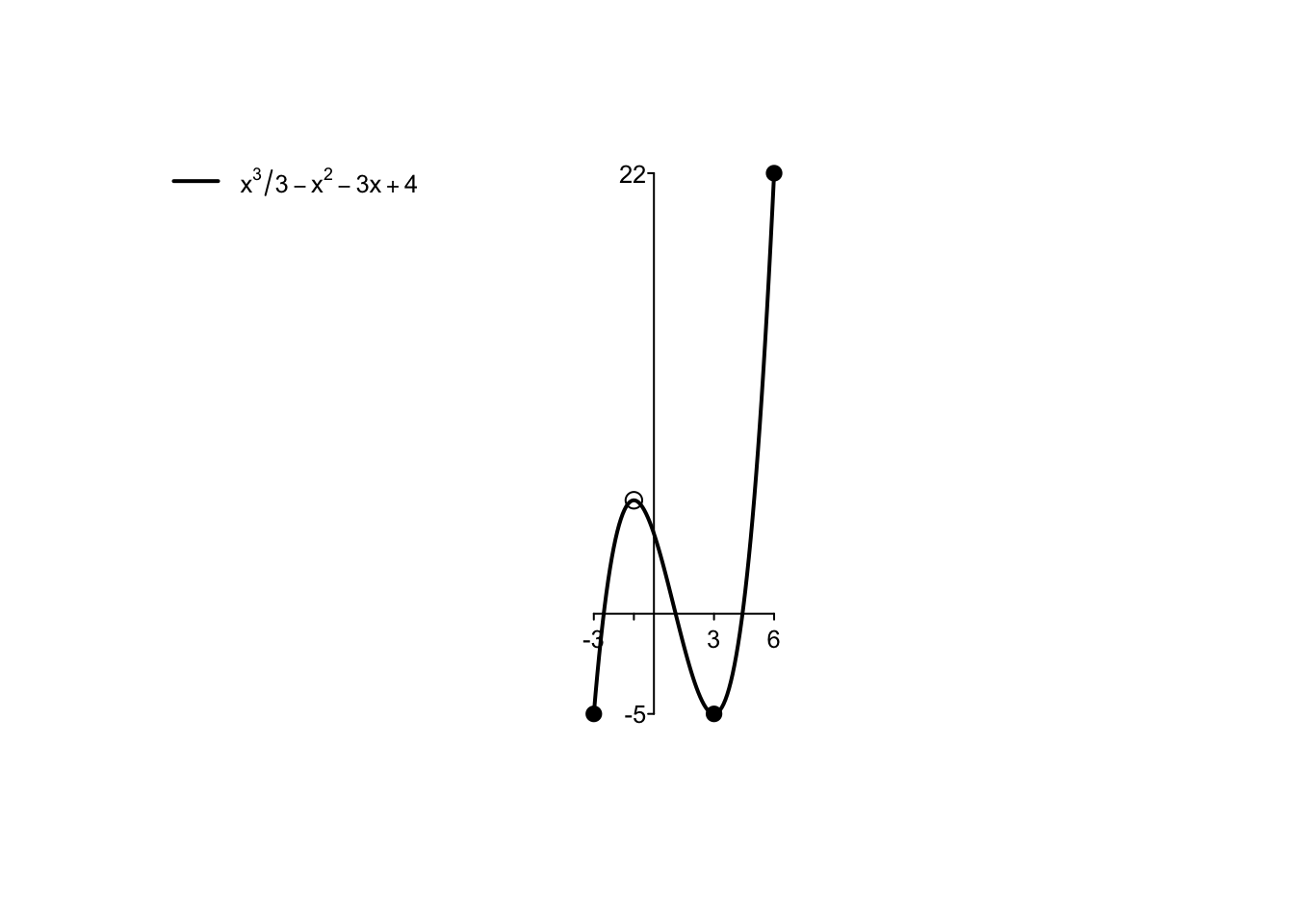
Se si considera la funzione dell’esempio precedente su tutta la retta reale, suo dominio naturale, essa risulta illimitata sia inferiormente che superiormente: \[\begin{align*} &\lim_{x \to -\infty} \frac{x^{3}}{3}-x^{2}-3x+4 = \lim_{x \to -\infty} \frac{x^{3}}{3} =-\infty,\\ &\lim_{x \to +\infty} \frac{x^{3}}{3}-x^{2}-3x+4 = \lim_{x \to +\infty} \frac{x^{3}}{3} =+\infty. \end{align*}\] Di conseguenza, la funzione $f:\mathbb{R} \to \mathbb{R},$ $f(x)=\frac{x^{3}}{3}-x^{2}-3x+4$, non possiede né massimo né minimo.

Per ottimizzare una funzione, si deve quindi sempre controllare quello che accade alla frontiera del suo dominio, includendo se possibile i limiti per $x \to \pm \infty$. Si noti infatti che si possono sempre cambiare i punti di minimo e massimo di una funzione semplicemente cambiandone il dominio.

5.4 Condizione del secondo ordine e punti di flesso

Laddove lo studio della derivata non fosse possibile o risultasse complesso, il calcolo della derivata seconda permette di dare una condizione aggiuntiva e sufficiente per l’esistenza di massimi/minimi. Si può infatti constatare come nell’intorno di un punto di massimo locale una funzione debba essere forzatamente concava, e nell’intorno di un punto di minimo locale una funzione debba essere forzatamente convessa. Si ha dunque il seguente teorema.

Theorem 5.4 (Condizione del secondo ordine per punti di massimo/minimo locali) Sia data la funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$ due volte derivabile nel punto $x_0 \in A$ stazionario ($f'(x_0)=0$) interno al suo dominio:

se $f''(x_0)<0$, allora $x_0$ è un punto di massimo locale;
se $f''(x_0)>0$, allora $x_0$ è un punto di minimo locale.

Si osservi come per ottenere condizioni sufficienti per l’esistenza di un massimo/minimo anche locale, si debba comunque ricavare una informazione migliore rispetto alla condizione del primo ordine, ovvero si debba o studiare il segno della derivata prima (come fatto nell’Esempio 5.4) oppure calcolare anche la derivata seconda.

Nel caso in cui anche la derivata seconda (oltre alla prima) si annulli in un punto stazionario, il Teorema 5.4 risulta inutilizzabile perché la funzione potrebbe cambiare la propria concavità nel punto, creando quello che viene detto un punto di flesso.

Definition 5.4 Sia data la funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$. Il punto interno $x_f \in A$ è detto punto di flesso per $f$ se in un suo intorno sinistro $I^-(x_f)$ $f$ è convessa (concava) e in un suo intorno destro $I^+(x_f)$ $f$ è concava (convessa).

Nei grafici delle funzioni di seguito, identificheremo i punti di flesso con un asterisco.

Ricordiamo dal Capitolo 4 che una funzione $f$ due volte derivabile è: convessa se e solo se ha derivata seconda non negativa $f''(x) \geq 0$; concava se e solo se possiede derivata seconda non positiva $f''(x) \leq 0$. In un punto di flesso, se la derivata seconda varia con continuità, essa quindi si annullerà.

Ad esempio, il punto $x=0$ è un punto di flesso per la funzione $f:\mathbb{R} \to \mathbb{R}$, $f(x)=x^3$. In questo punto, la funzione passa da concava a convessa, e di conseguenza la derivata seconda $f''(x)=6x$ da negativa a positiva, annullandosi in $x=0$.

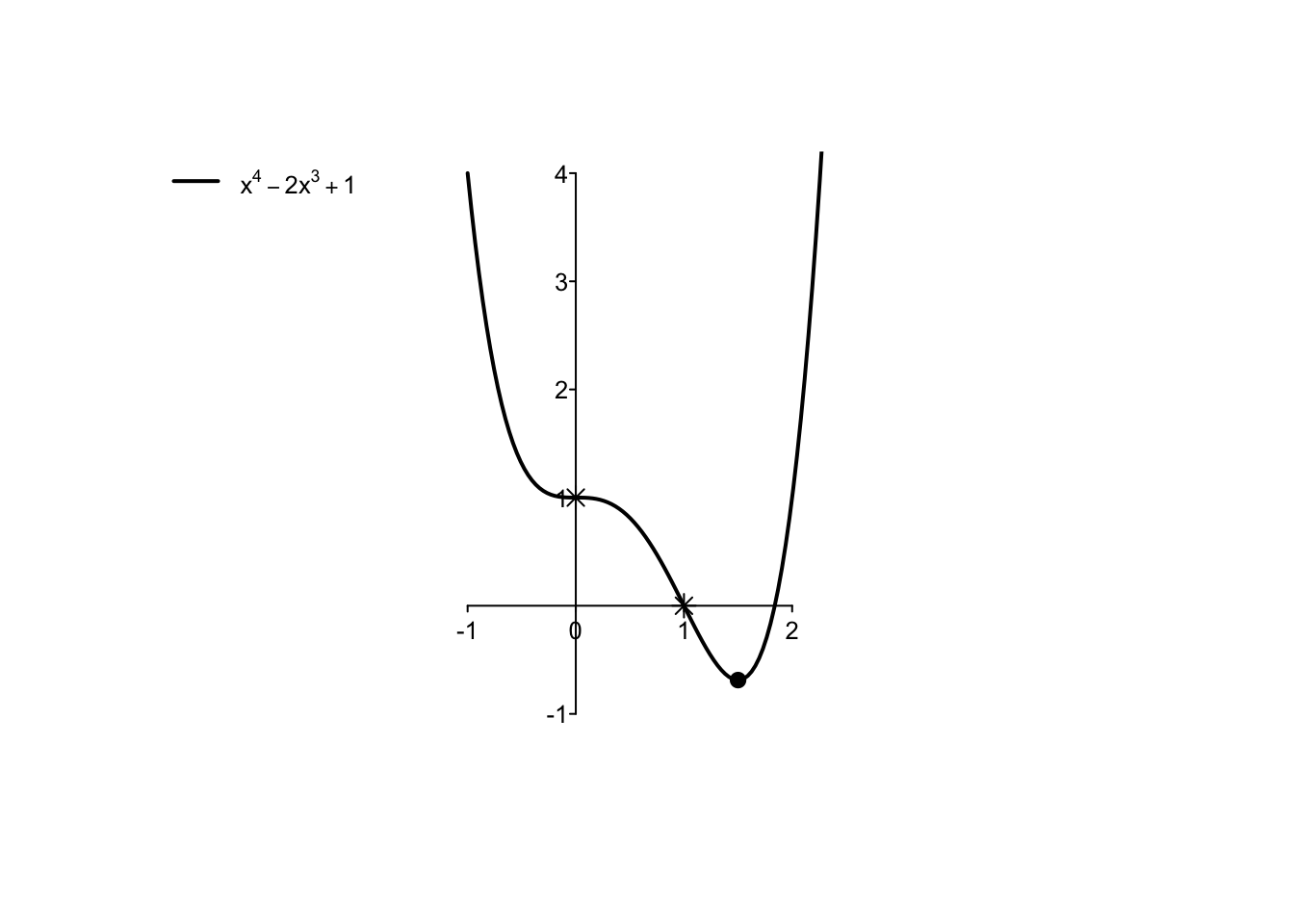
Example 5.5 Si dica se esistono e nel caso si calcolino punti di massimo e minimo assoluti della funzione $f:\mathbb{R} \to \mathbb{R}$, definita da \[ f(x)=x^{4}-2x^{3}+1. \] Si osserva immediatamente che, essendo la funzione un polinomio di quarto grado, essa non può ammettere massimo, in quanto \[\begin{align*} &\lim_{x \to -\infty} x^{4}-2x^{3}+1 = \lim_{x \to -\infty} x^{4} =+\infty,\\ &\lim_{x \to +\infty} x^{4}-2x^{3}+1 = \lim_{x \to +\infty} x^{4} =+\infty. \end{align*}\]

Si osservi che un qualsiasi polinomio (di grado 1 o superiore) non può ammettere sia massimo che minimo sul suo dominio naturale $\mathbb{R}$.

Il fatto che i due limiti di cui sopra siano pari a $+\infty$ e la continuità della funzione in oggetto implicano l’esistenza di un minimo (anche se non è applicabile il Teorema di Weierstrass), che dovrà forzatamente essere raggiunto su un punto stazionario interno.

Si calcola allora la derivata prima \[ f'(x)=4x^3-6x^2=2x^2 \, (2x-3), \] che si annulla nei punti stazionari $x_1=0$, $x_2=\frac{3}{2}$. Dato che \[ f'(x) \geq 0 \quad \text{per} \quad x \in \left[\frac{3}{2},+\infty\right), \] il punto $x_2$ risulta essere di minimo relativo. In un intorno completo del punto $x_1$ la funzione risulta invece sempre decrescente, quindi $x_1$ non è né un punto di massimo né di minimo.

Queste informazioni sono confermate dal calcolo della derivata seconda: \[ f''(x)=12x^2-12x=12x(x-1). \] Dato che $f''\left(\frac{3}{2}\right)>0$, la funzione è localmente convessa in $x_2=\frac{3}{2}$ che è un punto di minimo relativo, mentre $f''(0)=0$. In un intorno del punto $x_1=0$, la derivata seconda cambia di segno, quindi la funzione cambia la sua concavità passando da convessa a concava: esso è un punto di flesso (essendo stazionario è un punto di flesso a tangente orizzontale). Analogamente, anche $x=1$ è un punto di flesso, in cui la funzione passa da concava a convessa.

In conclusione, dal calcolo dei limiti a $\pm \infty$ la funzione non ammette massimo essendo illimitata superiormente. Di conseguenza, l’unico punto di minimo relativo trovato è il punto di minimo assoluto.

In conclusione, possiamo formulare una risposta alle domande che ci eravamo posti come obiettivo di questo capitolo.

Una funzione $f:A\subseteq \mathbb{R} \to \mathbb{R}$ può avere massimo/minimo assoluto:

nei punti stazionari interni al suo dominio;
nei punti di frontiera inclusi nel suo dominio.

Per determinare la natura di eventuali punti di massimo/minimo relativi, è in ogni caso necessario valutare il comportamento della funzione nei punti di frontiera (al loro limite, se non inclusi nel dominio) e se possibile al limite per $x \to \pm \infty$.

Se $A$ è un insieme chiuso e limitato (non è necessario che sia un intervallo) ed $f$ è continua, l’esistenza di massimo e minimo è garantita dal Teorema di Weierstrass.

5.5 Studio di funzione

Utilizzando tutti i concetti finora studiati è possibile disegnare il grafico di una qualsiasi funzione reale. Illustreremo i passaggi necessari tramite alcuni esempi.

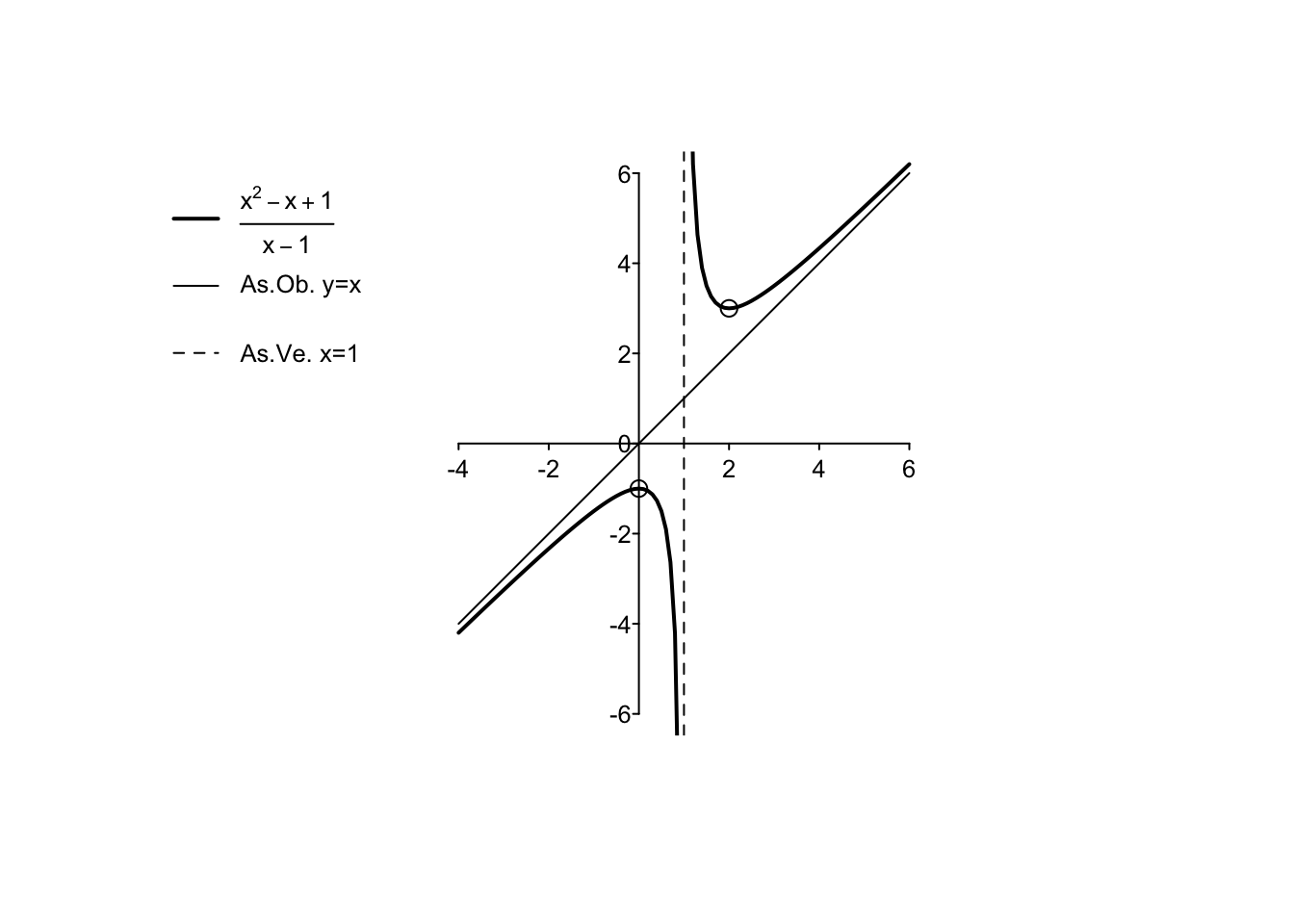
Example 5.6 Si disegni il grafico della funzione $f: D_f \to \mathbb{R},$ \[ f(x)=\frac{x^2-x+1}{x-1}. \] - Dominio naturale

Il dominio naturale della funzione in oggetto è ristretto rispetto alla retta reale per la presenza di una frazione il cui denominatore non può annullarsi. Ponendo $x-1 \neq 0$, si ottiene che \[ D_f=\mathbb{R} \setminus \{1\}. \]

Limiti nei punti di frontiera del dominio naturale (includendo $\pm \infty$)

Per $x \to \pm \infty$, si ha un rapporto tra funzioni infinite (B). Utilizzando il Teorema del Confronto degli Ordini di Infinito nel Capitolo 3, si ottiene \[\begin{align*} &\lim_{x \to -\infty} \, \frac{x^2-x+1}{x-1} = \lim_{x \to -\infty} \, \frac{x^2}{x} =\lim_{x \to -\infty} \, x=-\infty, \\ &\lim_{x \to +\infty} \, \frac{x^2-x+1}{x-1} = \lim_{x \to +\infty} \, \frac{x^2}{x} =\lim_{x \to +\infty} \, x=+\infty. \\ \end{align*}\] La funzione non ammette minimo o massimo assoluti essendo illimitata sia inferiormente che superiormente. È lecito chiedersi se il grafico della funzione ammetta un asintoto obliquo di equazione $y=mx+q$. Calcolando \[ m=\lim_{x \to +\infty} \, \frac{f(x)}{x}=\lim_{x \to +\infty} \, \frac{x^2-x+1}{x^2-x}=\lim_{x \to +\infty} \, \frac{x^2}{x^2}=1, \] e quindi \[\begin{align*} q=\lim_{x \to +\infty} \, f(x) -mx&=\lim_{x \to +\infty} \, \frac{x^2-x+1}{x-1}-x \\&=\lim_{x \to +\infty} \, \frac{x^2-x+1-x^2+x}{x-1}=\lim_{x \to +\infty} \, \frac{1}{x-1}=0, \end{align*}\] risulta l’asintoto obliquo $y=x$ per $x \to +\infty$. Si verifica immediatamente che lo stesso asintoto risulta anche per $x \to -\infty$.

Per quanto riguarda invece l’intorno del punto $x=1$, escluso dal dominio, si ha un limite di tipologia A, per cui in $x=1$ si ha un asintoto verticale con: \[ \lim_{x \to 1^-} \,\frac{x^2-x+1 (\mathbf{+})}{x-1\, (\mathbf{-})} = -\infty,\quad \lim_{x \to 1^+} \,\frac{x^2-x+1 (\mathbf{+})}{x-1\, (\mathbf{+})} = +\infty. \] È molto utile posizionare su una bozza del grafico finale le informazioni ricavate dal calcolo dei limiti e determinare qualitativamente la funzione più semplice che le verifica. La funzione “parte” da $-\infty$, e “ritorna” a $-\infty$ nell’intorno sinistro di $x=1$: deve quindi possedere almeno un punto di massimo relativo nell’intervallo $(-\infty,1)$. Analogamente, deve possedere almeno un punto di minimo relativo nell’intervallo $(1,+\infty)$, in cui “parte” da $+\infty$ e vi “ritorna”. Ci aspettiamo quindi di trovare almeno due punti stazionari dallo studio della derivata prima.

Questa analisi supplementare aiuta ad identificare immediatamente errori commessi in uno studio di una funzione. Lo studio di una funzione è un puzzle in cui tutti i pezzi si devono incastrare perfettamente. La incoerenza di una informazione rispetto a quanto ricavato in precedenza o quanto si ricaverà in futuro, è sintomo della presenza di un errore.

Studio del segno della derivata prima

Scrivendo \[ f(x)=\frac{x^2-x+1}{x-1}=\frac{x^2-(x-1)}{x-1}=\frac{x^2}{x-1}-1, \] si calcola \[ f'(x)=\left(\frac{x^2}{x-1}-1 \right)'=\frac{2x\,(x-1)-x^2\,(1)}{(x-1)^2}=\frac{2x^2-2x-x^2}{(x-1)^2}=\frac{x^2-2x}{(x-1)^2}=\frac{x(x-2)}{(x-1)^2}. \]

È sempre consigliabile scrivere la funzione nel modo che faciliti il più possibile il calcolo della derivata. Affidarsi sempre ed unicamente alle formule di derivazione senza verificare se la funzione può essere prima semplificata è una strategia perdente: aumenta i calcoli e, di conseguenza, la probabilità di errore.

Il denominatore della derivata è sempre positivo, mentre il numeratore ha due radici $x_1=0$, $x_2=2$ (due punti stazionari, come anticipato), per cui \[ f'(x) \geq 0 \quad \text{ per }\quad x \in (-\infty,0] \cup [2,+\infty). \] Dallo studio del segno della derivata si ricava che $x_1=0$ è un punto di massimo relativo (la funzione passa da crescente a decrescente), mentre $x_2=2$ è un punto di minimo relativo (la funzione passa da decrescente a crescente). Si osservi come queste informazioni siano perfettamente coerenti con quanto prima anticipato.

Cosa dobbiamo aspettarci dalla derivata seconda? Provando a disegnare il grafico della funzione, è facile verificare che la funzione più semplice che rispetti limiti e segno della derivata è concava nell’intervallo $(-\infty,1)$, convessa nell’intervallo $(1,+\infty)$.

Studio del segno della derivata seconda

Scrivendo \[ f'(x)=\frac{x^2-2x}{(x-1)^2}=\frac{x^2-2x+1-1}{(x-1)^2}=\frac{(x-1)^2}{(x-1)^2}-\frac{1}{(x-1)^2}=1-(x-1)^{-2}, \] si ottiene \[ f''(x)=-(-2(x-1)^{-3})=2(x-1)^{-3}=\frac{2}{(x-1)^3}. \] Il segno della derivata seconda dipende esclusivamente dal denominatore, per cui \[ f''(x) >0 \quad \text{ per } \quad x \in (1,+\infty). \]

È un errore grave affermare che $x=1$ è un punto di flesso per la funzione, in quanto la funzione è concava alla sua sinistra e convessa alla sua destra. Il punto $x=1$ non fa nemmeno parte del dominio naturale della funzione.

Grafico

Utilizzando tutte le informazioni raccolte, è possibile disegnare il grafico della funzione.

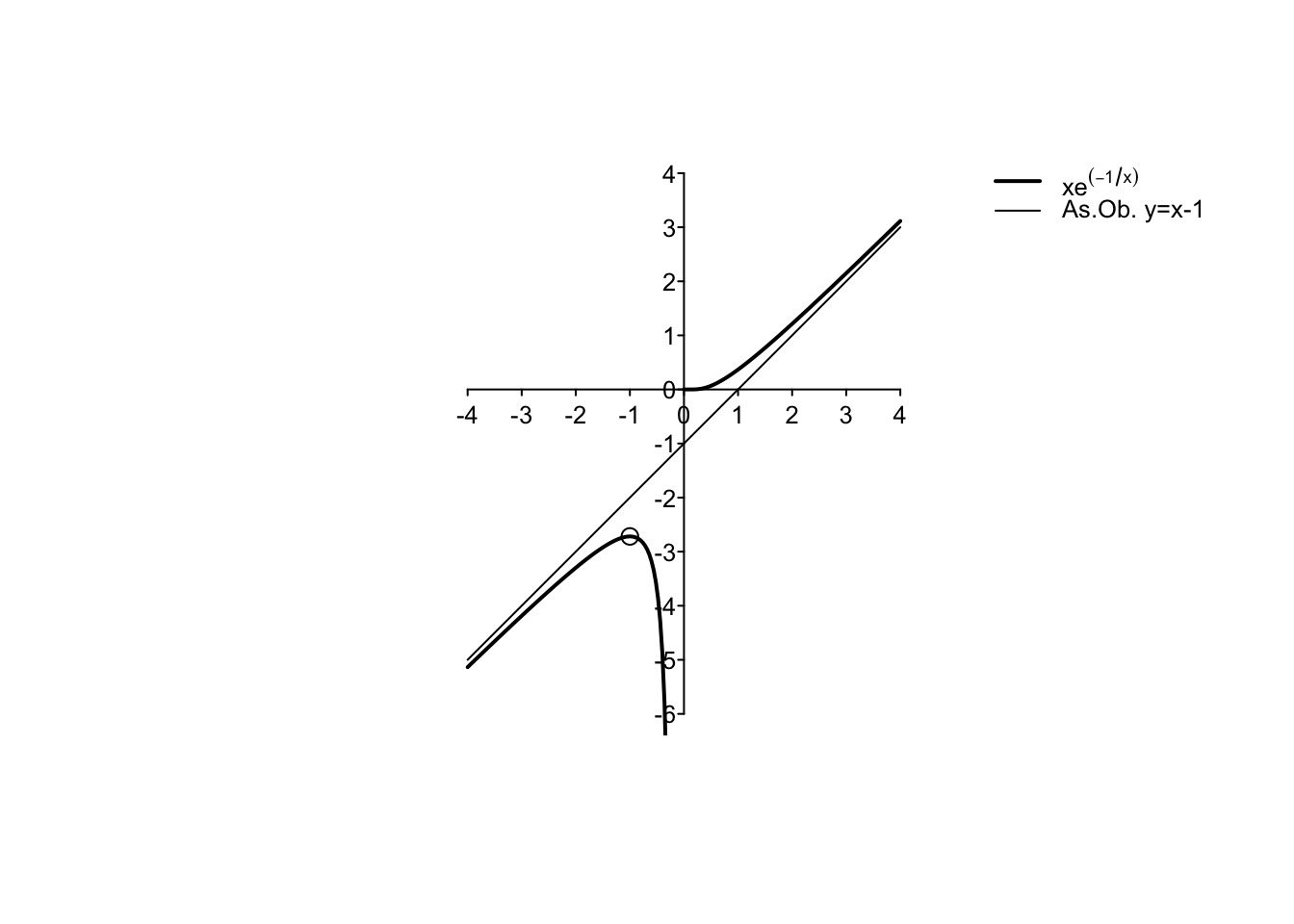
Example 5.7 Si disegni il grafico della funzione $f: D_f \to \mathbb{R},$ \[ f(x)=x\,e^{-\frac1x}. \]

Dominio naturale

Il dominio naturale della funzione in oggetto è ristretto rispetto alla retta reale per la presenza di una frazione il cui denominatore non può annullarsi. Si ottiene quindi \[ D_f=\mathbb{R} \setminus \{0\}. \]

Limiti nei punti di frontiera del dominio naturale (includendo $\pm \infty$)

Per $x \to \pm \infty$, non si hanno forme indeterminate e si calcola immediatamente che \[ \lim_{x \to +\infty} x\,e^{-\frac1x}=+\infty \cdot e^0 = +\infty \cdot 1 =+\infty, \quad \lim_{x \to -\infty} x\,e^{-\frac1x}=-\infty \cdot e^0 = -\infty \cdot 1 =-\infty. \] È lecito chiedersi se il grafico della funzione ammetta un asintoto obliquo di equazione $y=mx+q$. Calcolando \[ m=\lim_{x \to +\infty} \, \frac{f(x)}{x}=\lim_{x \to +\infty} \, e^{-\frac1x}=e^0=1, \] si trova il coefficiente angolare. Per l’intercetta, si deve risolvere \[ q=\lim_{x \to +\infty} \, f(x) -mx=\lim_{x \to +\infty} x\,e^{-\frac1x} -x =\lim_{x \to +\infty} x\,(e^{-\frac1x}-1). \] Questa è una forma che può essere trattata con de l’Hôpital (D) scrivendo \[ q=\lim_{x \to +\infty} x\,(e^{-\frac1x}-1) = \lim_{x \to +\infty} \, \frac{e^{-\frac1x}-1}{\frac{1}{x}}. \] Derivando numeratore e denominatore si ottiene \[ q=\lim_{x \to +\infty} \, \frac{e^{-\frac1x}-1}{\frac{1}{x}} = \lim_{x \to +\infty} \, \frac{\frac{1}{x^2}e^{-\frac1x}}{-\frac{1}{x^2}}=\lim_{x \to +\infty} \,-e^{-\frac1x}=-1. \] Risulta quindi l’asintoto obliquo $y=x-1$ per $x \to +\infty$. Si verifica immediatamente che lo stesso asintoto risulta anche per $x \to -\infty$.

Per quanto riguarda invece l’intorno sinistro del punto $x=0$, escluso dal dominio, si ha una forma indeterminata del tipo $0\cdot (+\infty)$, che si può risolvere ancora con de l’Hôpital (D): \[ \lim_{x \to 0^-} x\,e^{-\frac1x} =\lim_{x \to 0^-} \, \frac{e^{-\frac1x}}{\frac{1}{x}}=\lim_{x \to 0^-} \, \frac{\frac{1}{x^2}e^{-\frac1x}}{-\frac{1}{x^2}}=\lim_{x \to 0^-}-e^{-\frac1x}=-\infty. \] Nell’intorno destro di $x=0$, non si ha una forma indeterminata in quanto \[ \lim_{x \to 0^+} x\,e^{-\frac1x}=0 \cdot 0=0. \] Dai limiti calcolati, si deduce che la funzione “parte” da $-\infty$ e “ritorna” a $-\infty$ nell’intorno sinistro di $x=0$: deve quindi possedere almeno un punto di massimo relativo nell’intervallo $(-\infty,0)$. A destra di $x=0$ la funzione “parte” da $0$ per diventare arbitrariamente grande, quindi potrebbe risultare sempre crescente. Ci aspettiamo quindi di trovare almeno un punto stazionario dallo studio della derivata prima.

Studio del segno della derivata prima

Si calcola \[ f'(x)=1\cdot e^{-\frac1x}+x\frac{1}{x^2}e^{-\frac1x}=e^{-\frac1x}\left(1+\frac1x\right)=e^{-\frac1x}\left(\frac{x+1}{x}\right). \] Dato che una funzione esponenziale è sempre positiva, il segno della derivata prima dipende dalla frazione tra parentesi, per cui si calcola \[ f'(x) \geq 0 \quad \text{ per }\quad x \in (-\infty,-1] \cup (0,+\infty). \] Dallo studio del segno della derivata si ricava che $x_1=-1$ è un punto di massimo relativo (la funzione passa da crescente a decrescente), coerentemente con quanto atteso. Si osservi che nulla si può dire di $x=0$ che è escluso dal dominio naturale della funzione.

Studio del segno della derivata seconda

Ricordando che \[ f'(x)=e^{-\frac1x}\left(1+\frac1x\right), \] si ottiene \[ f''(x)=\frac{1}{x^2}e^{-\frac1x}\left(1+\frac1x\right)+e^{-\frac1x}\left(\frac{-1}{x^2}\right)=\frac{e^{-\frac1x}}{x^2}\left(1+\frac1x-1\right)=\frac{e^{-\frac1x}}{x^3}. \] Il segno della derivata seconda dipende esclusivamente dal denominatore, per cui si ottiene \[ f''(x) >0 \quad \text{ per } \quad x \in (0,+\infty). \]

Grafico

Utilizzando tutte le informazioni raccolte, è possibile disegnare il grafico della funzione sotto studio. Il grafico della funzione “parte” dall’origine degli assi con tangente orizzontale, essendo $\lim_{x \to 0^+} f'(x)=0$.

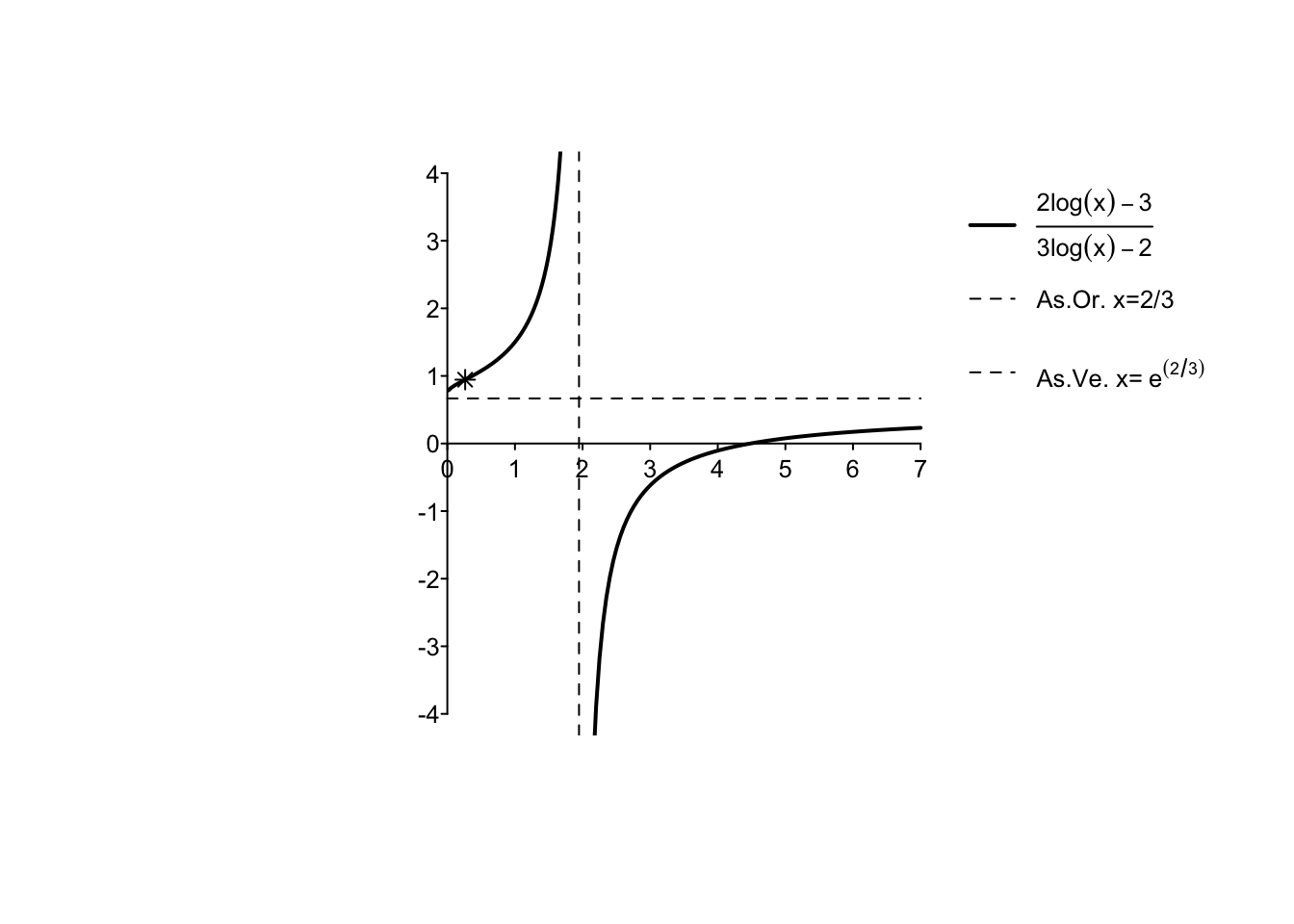
Example 5.8 Si disegni il grafico della funzione $f: D_f \to \mathbb{R},$ \[ f(x)=\frac{2\log(x) -3}{3 \log(x) -2}. \]

Dominio naturale

Il dominio naturale della funzione in oggetto è ristretto rispetto alla retta reale per la presenza di due logaritmi che devono possedere un argomento positivo ($x>0$) e una frazione, il cui denominatore non può annullarsi: \[ 3 \log(x) \neq 2 \quad \Rightarrow \quad x \neq e^{\frac{2}{3}}. \] Si ha dunque: \[ D_f=\left(0,e^{\frac{2}{3}}\right) \cup \left(e^{\frac{2}{3}},+\infty\right). \]

Limiti nei punti di frontiera del dominio naturale (includendo $+\infty$)

Per $x \to 0^+$ e $x \to + \infty$, si ha un rapporto tra funzioni infinite (B) dello stesso ordine: \[ \lim_{x \to +\infty} \, \frac{2\log(x) -3}{3 \log(x) -2} = \lim_{x \to +\infty} \, \frac{2\log(x)}{3 \log(x)} = \frac{2}{3}, \quad \lim_{x \to 0^+} \, \frac{2\log(x) -3}{3 \log(x) -2} = \lim_{x \to 0^+} \, \frac{2\log(x)}{3 \log(x)} = \frac{2}{3}. \] Il grafico della funzione ha quindi un asintoto orizzontale per $x \to +\infty$. Per quanto riguarda invece l’intorno del punto $x=e^{\frac{2}{3}}$, escluso dal dominio, si ha un limite di tipologia A, per cui si ha un asintoto verticale con: \[ \lim_{x \to {e^{\frac{2}{3}}}^-} \,\frac{2\log(x) -3\,(-)}{3 \log(x) -2\,(-)}=+\infty,\quad \lim_{x \to {e^{\frac{2}{3}}}^+} \,\frac{2\log(x) -3\,(-)}{3 \log(x) -2\,(+)}=-\infty. \]

Riportando su una bozza del grafico finale le informazioni ricavate dal calcolo dei limiti, non si ricava la necessità che la funzione abbia punti di massimo o minimo relativi. La funzione “parte” da $2/3$, e diventa arbitrariamente grande a sinistra del suo asintoto verticale. Nell’intorno destro dell’asintoto,“parte” da $-\infty$ e quindi potrebbe semplicemente crescere verso l’asintoto orizzontale. Non ci aspettiamo quindi di trovare punti stazionari dallo studio della derivata prima in quanto la funzione potrebbe risultare essere sempre crescente, sia a sinistra che a destra del suo asintoto verticale.

Studio del segno della derivata prima

Si calcola \[\begin{align*} f'(x)&=\frac{\frac{2}{x}(3 \log(x) -2) - (2 \log(x) -3)\frac{3}{x} }{(3 \log(x) -2)^2}\\ &=\frac{6 \log(x) -4 -6 \log(x) +9 }{x\,(3 \log(x) -2)^2}=\frac{5 }{x\,(3 \log(x) -2)^2}. \end{align*}\] Il segno della derivata prima dipende esclusivamente dal fattore $x$ che è sempre positivo nel dominio naturale della funzione. Come anticipato, quindi si ha che \[ f'(x) >0, \quad x \in D_f. \]

Si ricordi che lo studio del segno della derivata prima e seconda deve avvenire sul dominio naturale della funzione.

Cosa dobbiamo aspettarci dalla derivata seconda? Provando a disegnare il grafico della funzione, è facile verificare che la funzione più semplice che rispetti limiti e segno della derivata è convessa a sinistra dell’asintoto verticale, e concava alla sua destra. Anche se non ci aspettiamo dei punti di flesso, vedremo dallo studio della derivata seconda, che la funzione ne possiede uno.

Studio del segno della derivata seconda

Scrivendo la derivata prima come un prodotto \[ f'(x)=\frac{5 }{x\,(3 \log(x) -2)^2}= 5 x^{-1} (3 \log(x) -2)^{-2}, \] si ottiene \[\begin{align*} f''(x)&=5\left[ -x^{-2} (3 \log(x) -2)^{-2} + x^{-1}\left(-2\,(3 \log(x) -2)^{-3}\,3\,x^{-1}\right) \right] \\&=5\left( -x^{-2} (3 \log(x) -2)^{-2} -6x^{-2} (3 \log(x) -2)^{-3}\right)\\ &=-5x^{-2}(3 \log(x) -2)^{-3}\left(3 \log(x) -2 +6 \right)=\frac{-5(3 \log(x) +4)}{x^2\,(3 \log(x) -2)^3}. \end{align*}\] Studiando il segno della derivata seconda, ci si accorge che il numeratore cambia di segno nel punto $x=e^{\frac{-4}{3}}$. Infatti si ha \[ f''(x) >0 \quad \text{ per } \quad x \in \left[e^{\frac{-4}{3}},e^{\frac{2}{3}}\right). \] La funzione presenta un punto di flesso in $x=e^{\frac{-4}{3}}$, dove passa da concava a convessa.

Il fatto che la funzione possegga un flesso non è in disaccordo con le informazioni reperite dalla derivata prima. Rimane utile cercare di capire il numero minimo di punti di massimo/minimo o punti di flesso che una funzione può avere, fermo restando che la funzione può sempre rivelarsi più complessa.

Grafico

Utilizzando tutte le informazioni raccolte, è possibile disegnare il grafico della funzione sotto studio. Si osservi che il punto $x=0$ non è propriamente un punto di minimo relativo in quanto non è interno al dominio (ne esiste solo un intorno destro). La funzione “parte” da $x=0$ con tangente verticale, in quanto $\lim_{x \to 0^+}f'(x)=+\infty$.

5.6 Esercizi

Si studino le seguenti funzioni $f: D_f \to \mathbb{R}$, in particolare ricavandone:

il dominio naturale $D_f$;
i limiti nei punti di frontiera del dominio naturale (includendo quando possibile $\pm \infty$);
la derivata prima $f'(x)$ e per quale insieme di punti si ha $f'(x) \geq 0$;
la derivata seconda $f''(x)$ e per quale insieme di punti si ha $f''(x) \geq 0$;
il grafico approssimativo con l’indicazione di eventuali punti di massimo/minimo relativi/assoluti, punti di flesso ed eventuali asintoti orizzontali, verticali, obliqui.

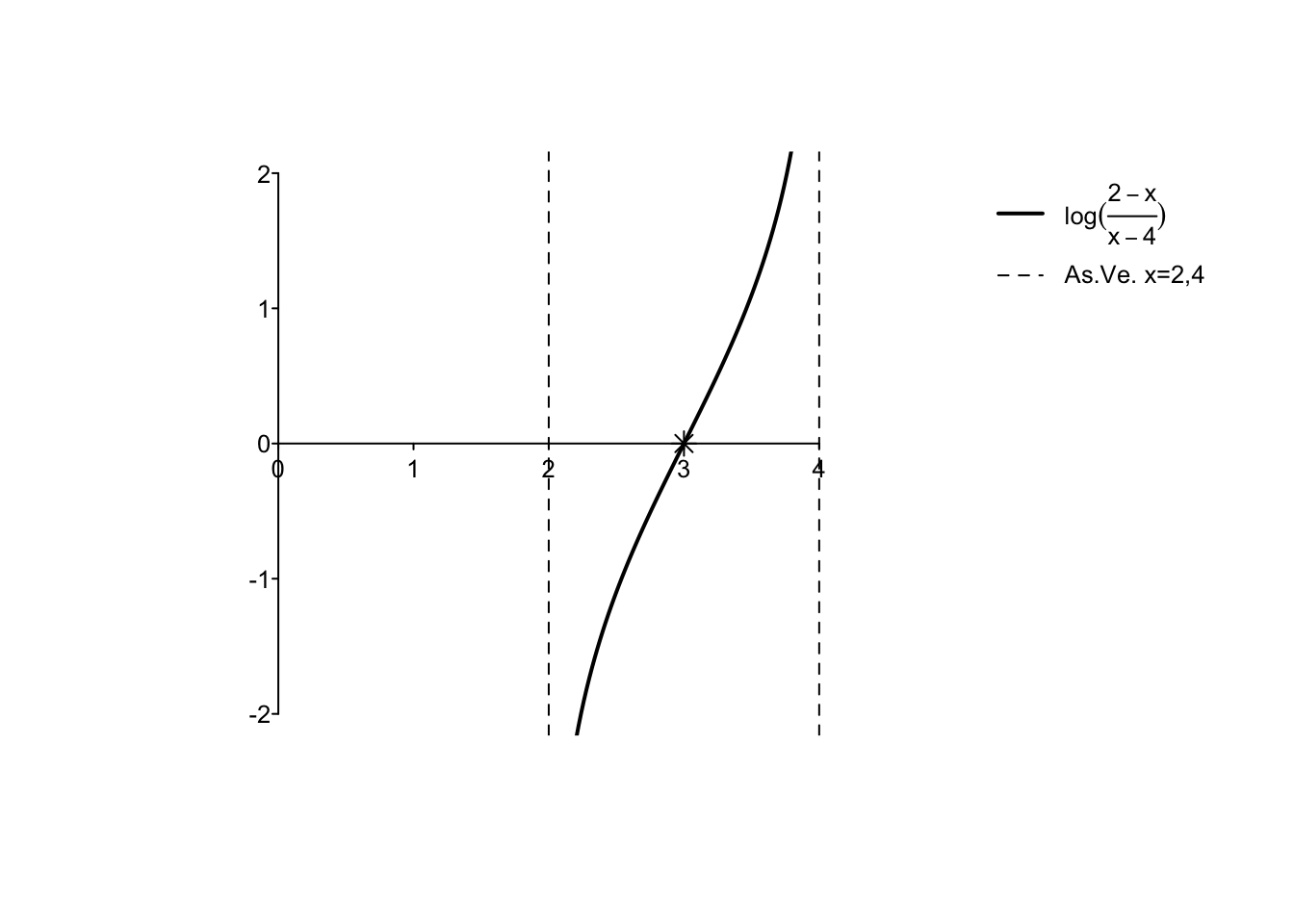
Exercise 5.1 \[ f(x)= \log \left( \frac{2-x}{x-4} \right) \]

$D_f=(2,4)$;
$\lim_{x\to 2^+} f(x)=-\infty,\lim_{x\to 4^-} f(x)=+\infty$;
$f'(x)= -\frac{2}{{x^2-6x+8}} \geq 0, \text{ per $x \in (2,4) $}$;
$f''(x)=\frac{4(x-3)}{(x^2-6x+8)^2}\geq 0, \text{ per $x \in [3,4)$}$;
grafico:

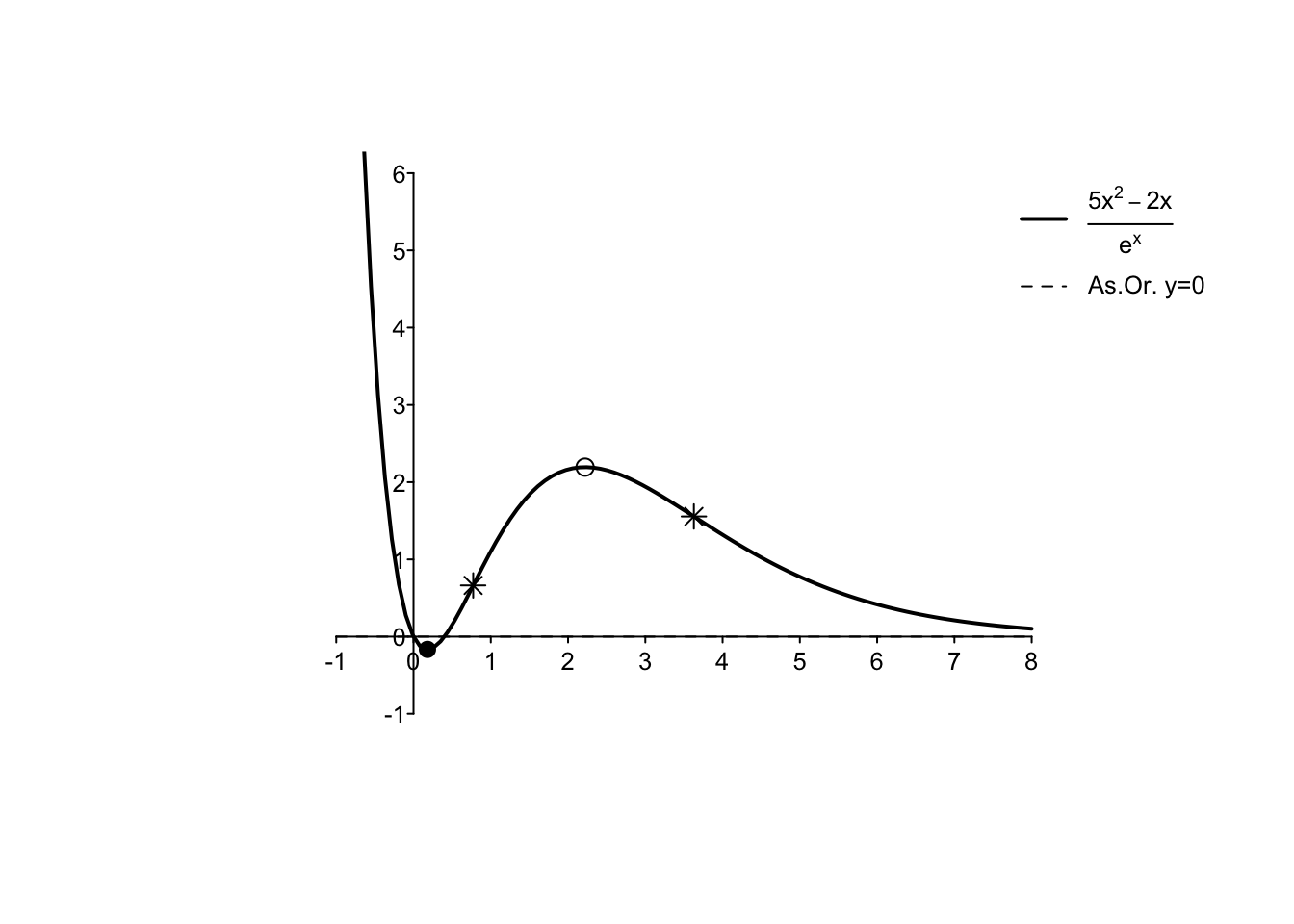
Exercise 5.2 \[ f(x)= \frac{5x^2-2x}{e^x} \]

$D_f=\mathbb{R}$;
$\lim_{x\to -\infty} f(x)=+\infty,\lim_{x\to+\infty} f(x)=0$;
$f'(x)= \frac{-5x^2+12x-2}{e^x} \geq 0, \text{ per $x \in [(6-\sqrt{26})/5, (6+\sqrt{26})/5]$}$;
$f''(x)=\frac{5x^2-22x+14}{e^x} \geq 0, \text{ per $x \in (-\infty,(11-\sqrt{51})/5] \cup [(11+\sqrt{51})/5,+\infty)$}$;
grafico:

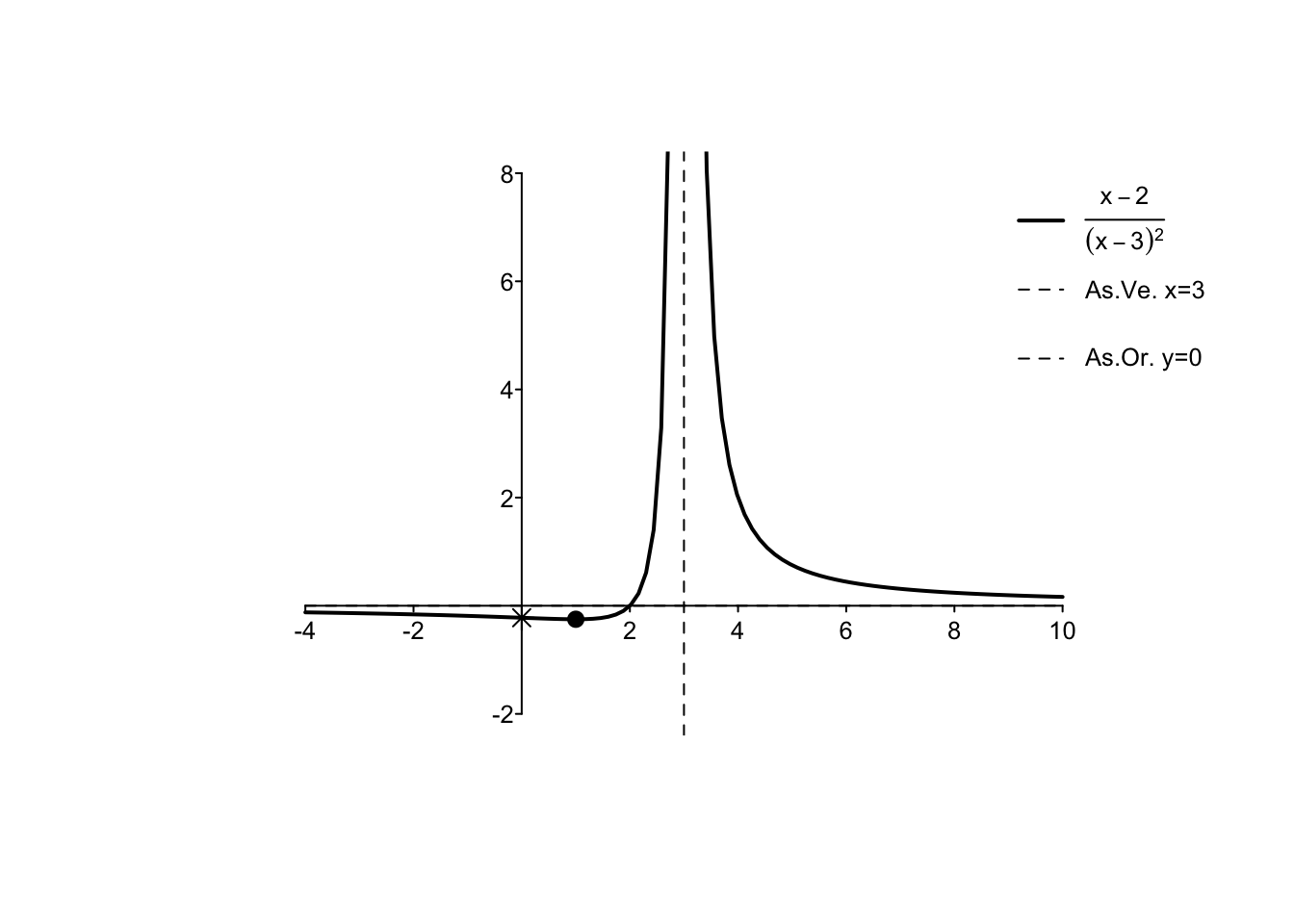
Exercise 5.3 \[ f(x)= \frac{(x-2)}{(x-3)^2} \]

$D_f=\mathbb{R}\setminus \{3\}$;
$\lim_{x\to -\infty} f(x)=\lim_{x\to +\infty} f(x)=0,\lim_{x\to 3} f(x)=+\infty$;
$f'(x)= \frac{1-x}{(x-3)^3} \geq 0, \text{ per $x \in [1,3)$}$;
$f''(x)=\frac{2x}{(x-3)^4} \geq 0, \text{ per $x \in[0,3)\cup (3,+\infty)$}$;

grafico:

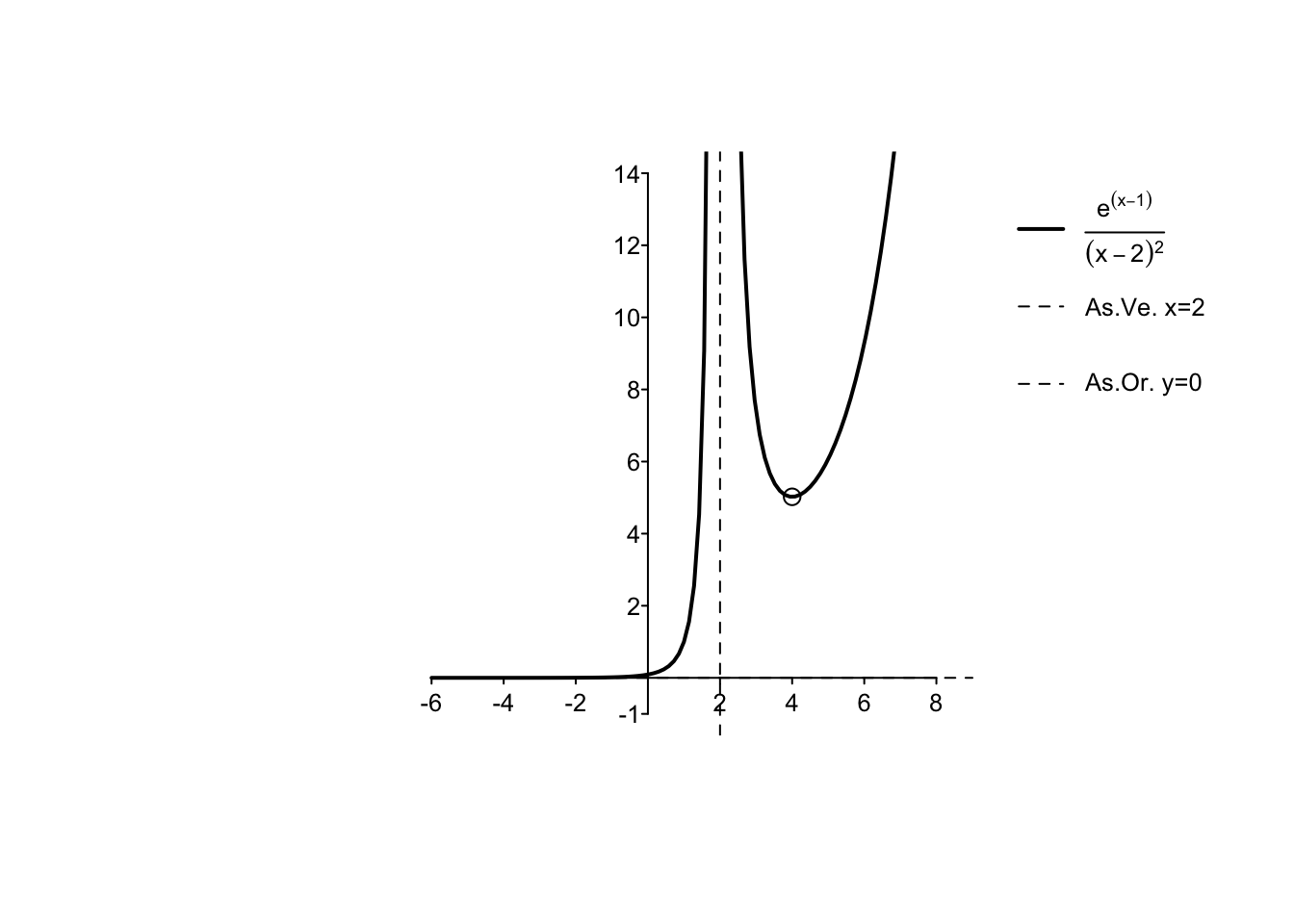
Exercise 5.4 \[ f(x)= \frac{e^{x-1}}{(x-2)^2} \]

$D_f=\mathbb{R}\setminus \{2\}$;
$\lim_{x\to -\infty} f(x)=0,\lim_{x\to 2} f(x)=+\infty, \lim_{x\to +\infty} f(x)=+\infty$;
$f'(x)=\frac{e^{x-1}(x-4)}{(x-2)^3}\geq 0, \text{ per } x \in (-\infty,2) \cup [4,+\infty)$;
$f''(x)=\frac{e^{x-1}(x^2-8x+18)}{(x-2)^4}, \text{ per } x \in D_f$;
grafico:

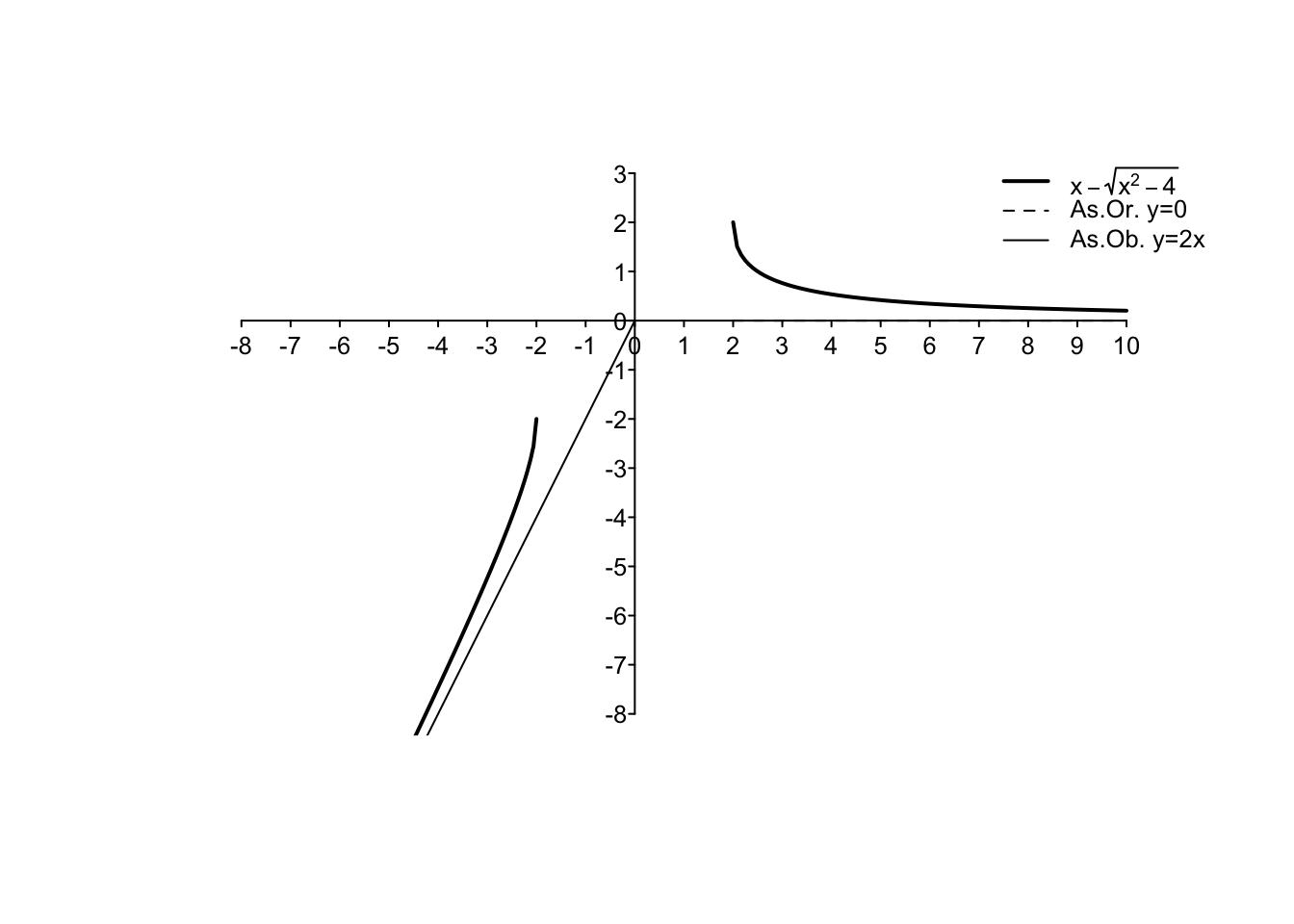
Exercise 5.5 \[ f(x)= x-\sqrt{x^2-4} \]

$D_f=(-\infty,-2] \cup [2,+\infty)$;
$\lim_{x\to -\infty} f(x)=-\infty,\lim_{x\to +\infty} f(x)=0,\lim_{x\to -2^-} f(x)=-2, \lim_{x\to 2^+} f(x)=2$;
$f'(x)= 1-\frac{x}{\sqrt{x^2-4}} \geq 0, \text{ per $x \in (-\infty,-2)$}$;
$f''(x)=\frac{4}{(x^2-4)^{3/2}}\geq 0, \text{ per $x \in D_f \setminus \{-2,2\}$}$;
grafico:

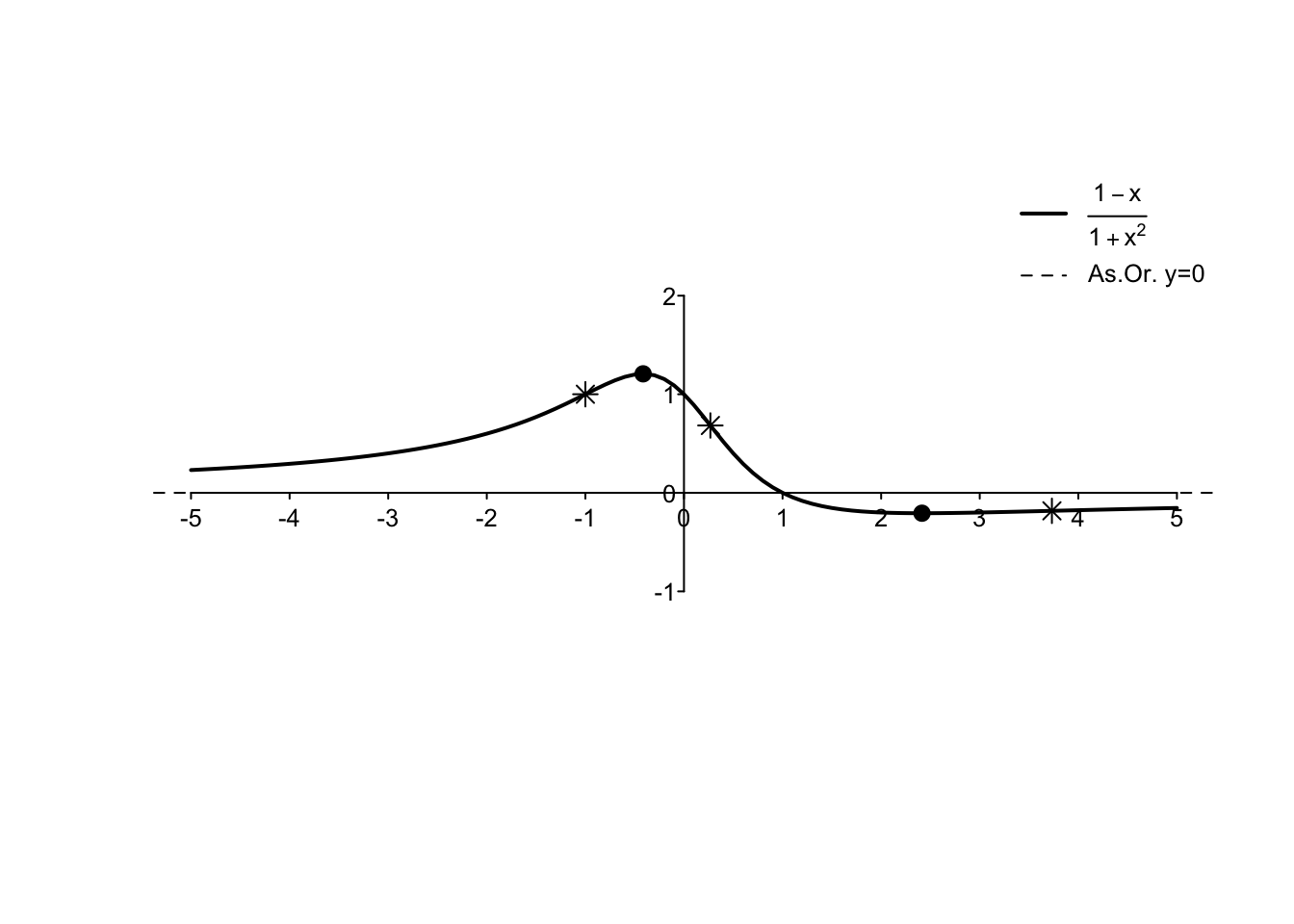
Exercise 5.6 \[ f(x)= \frac{1-x}{1+x^2} \]

$D_f=\mathbb{R}$;
$\lim_{x\to - \infty} f(x)=0,\lim_{x\to +\infty} f(x)=0$;
$f'(x)=\frac{x^2-2x-1}{(1+x^2)^2}\geq 0, \text{ per $x \in (-\infty, 1-\sqrt{2} ] \cup [1+\sqrt{2}, + \infty)$}$;
$f''(x)=-\frac{2(x+1)(x^2-4x+1)}{(1+x^2)^3} \geq 0, \text{ per $x \in (-\infty,-1] \cup [2-\sqrt{3},2+\sqrt{3}]$ }$;

grafico:

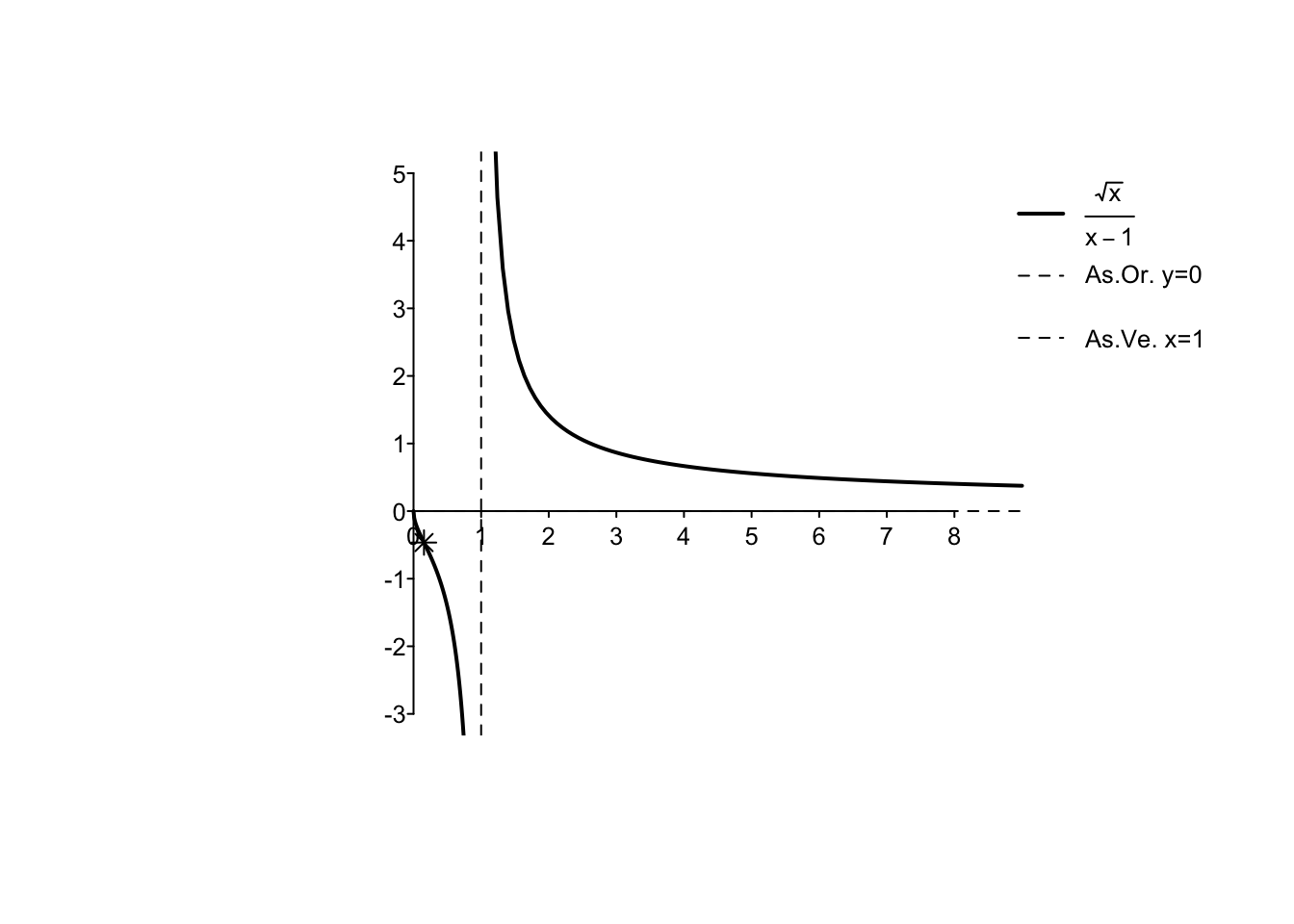
Exercise 5.7 \[ f(x)= \frac{\sqrt{x}}{x-1} \]

$D_f=[0,1) \cup (1,+\infty)$;
$\lim_{x\to 0^+} f(x)=0, \lim_{x\to 1^-} f(x)=-\infty,\lim_{x\to 1^+} f(x)=+\infty,\lim_{x\to +\infty} f(x)=0$;
$f'(x)=-\frac{x+1}{2\sqrt{x}(x-1)^2} \geq 0, \text{ mai per $x \in D_f $}$;
$f''(x)=\frac{3x^2+6x-1}{4x^{3/2}(x-1)^3} \geq 0, \text{ per $x \in (0,\frac{2\sqrt{3}-3}{3}] \cup (1,+\infty)$}$;
grafico: