2 Le funzioni elementari
Questo capitolo fornisce una panoramica delle cosiddette funzioni elementari, attraverso le quali possono essere costruite tutte le funzioni reali (di maggiore complessità) che verranno trattate nel seguito.
Dato un numero reale \(x \in \mathbb{R}\) e un naturale \(n \in \mathbb{N}\), \(x^n\) denota la \(n\)-ma potenza di \(x\), ovvero il prodotto di \(x\) per se stesso \(n\) volte. Per \(n,m \in \mathbb{N}\), si ha \[ x^{n+m}=x^n\,x^m. \] Per \(x \neq 0\), si definisce inoltre la \(n\)-ma potenza negativa come \(x^{-n}=\frac{1}{x^n}\); inoltre, si pone \(x^0=1\). Si osservi che la regola \(x^{n+m}=x^n\,x^m\) è così estesa, per \(x \neq 0\), a tutti gli interi \(n,m \in \mathbb{Z}\).
2.1 Funzioni lineari
Le funzioni reali del tipo \(f: \mathbb{R} \to \mathbb{R},\) \[ f(x)=mx+q, \quad m,q \in \mathbb{R}, \] sono dette funzioni lineari ed hanno come grafico una retta. Le funzioni lineari sono la famiglia più semplice di funzioni che possano essere sia crescenti che decrescenti.
Come già osservato, una funzione e il suo grafico sono due oggetti matematici distinti. Tuttavia, nel linguaggio comune, per identificare una funzione si può per metonimia utilizzare il suo grafico; ad esempio, nel seguito, per identificare una funzione lineare si potrà semplicemente parlare di una retta.
Una funzione lineare dipende da due parametri:
l’intercetta \(q\), che identifica l’intersezione con l’asse delle ordinate, \(q=f(0)\);
il coefficiente angolare \(m\), che determina la monotonia della funzione: un coefficiente angolare positivo \(m>0\) corrisponderà ad una funzione lineare (retta) strettamente crescente; un coefficiente angolare negativo \(m<0\) corrisponderà ad una funzione lineare (retta) strettamente decrescente; un coefficiente angolare nullo \(m=0\) corrisponderà ad una funzione lineare (retta) costante (sia crescente che decrescente).
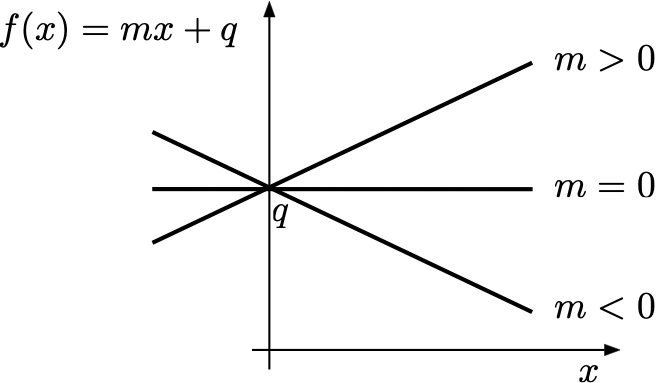
Sia nel caso di retta crescente che di retta decrescente, valori assoluti (cioè non considerandone il segno) più grandi del coefficiente angolare corrispondono ad inclinazioni più marcate della retta, valori assoluti più vicini allo zero a pendenze più lievi.
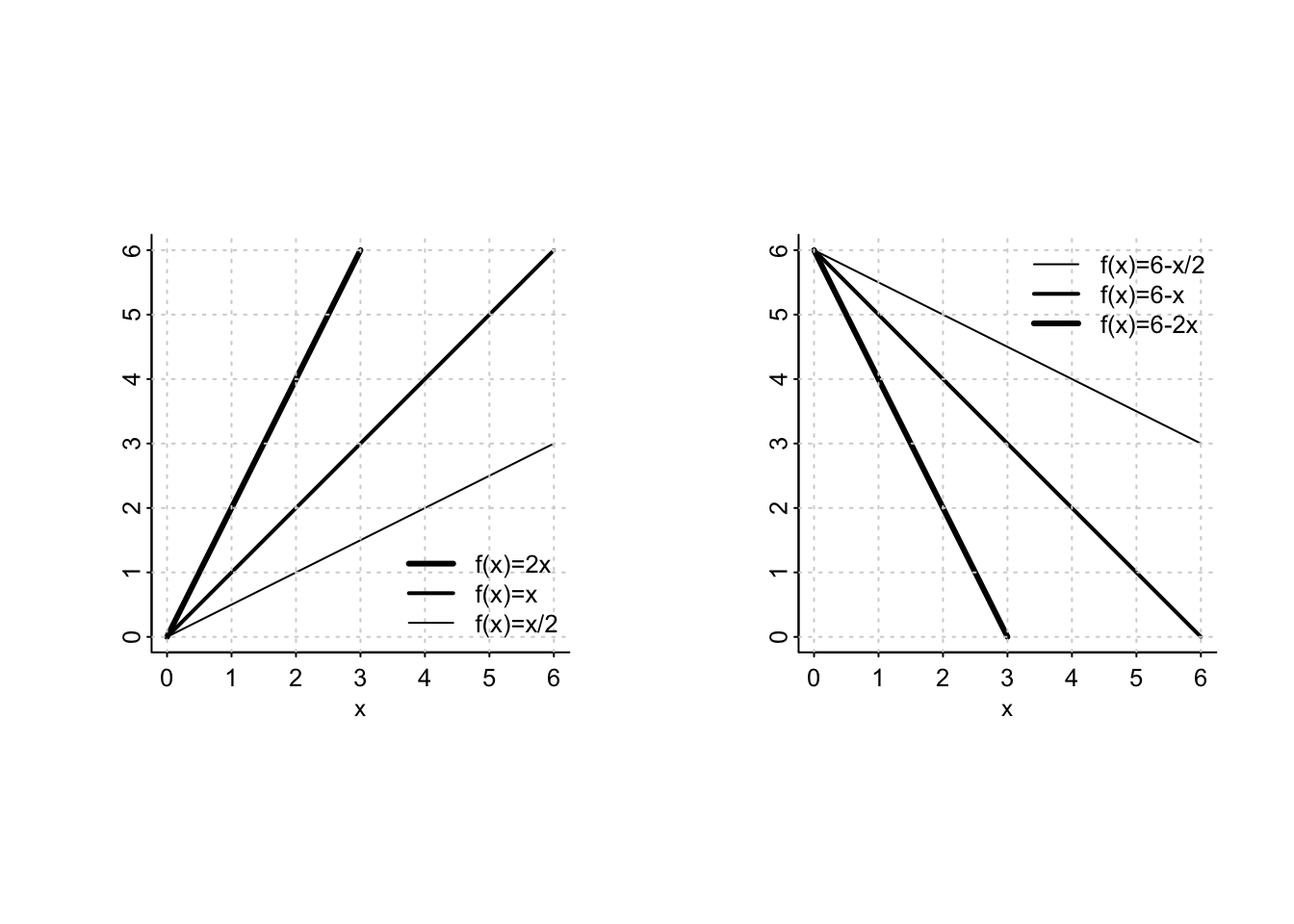
Si osserva immediatamente dalla definizione che una funzione lineare è (l’unica funzione ad essere) sia convessa che concava.
Ricordiamo come disegnare una retta e risolvere la corrispondente equazione/disequazione di primo grado nel seguente esempio.
Example 2.1 Si consideri la funzione \(f:\mathbb{R} \to \mathbb{R},\) \[f(x)= -3x+2.\]
Dalla sua forma analitica, si deduce che \(f\) è una retta strettamente decrescente.
Per dise-gnarla, basta identificare due punti appartenenti al suo grafico, come ad esempio
le due intersezioni con gli assi cartesiani. L’intersezione con l’asse delle ordinate è data dall’intercetta
\(f(0)=2\), mentre quella con l’asse delle ascisse dalla soluzione della associata equazione di primo grado
\[
-3x+2=0 \Rightarrow x=\frac{2}{3}.
\]
Con queste informazioni, si procede a disegnare il grafico della retta, come nella figura seguente.
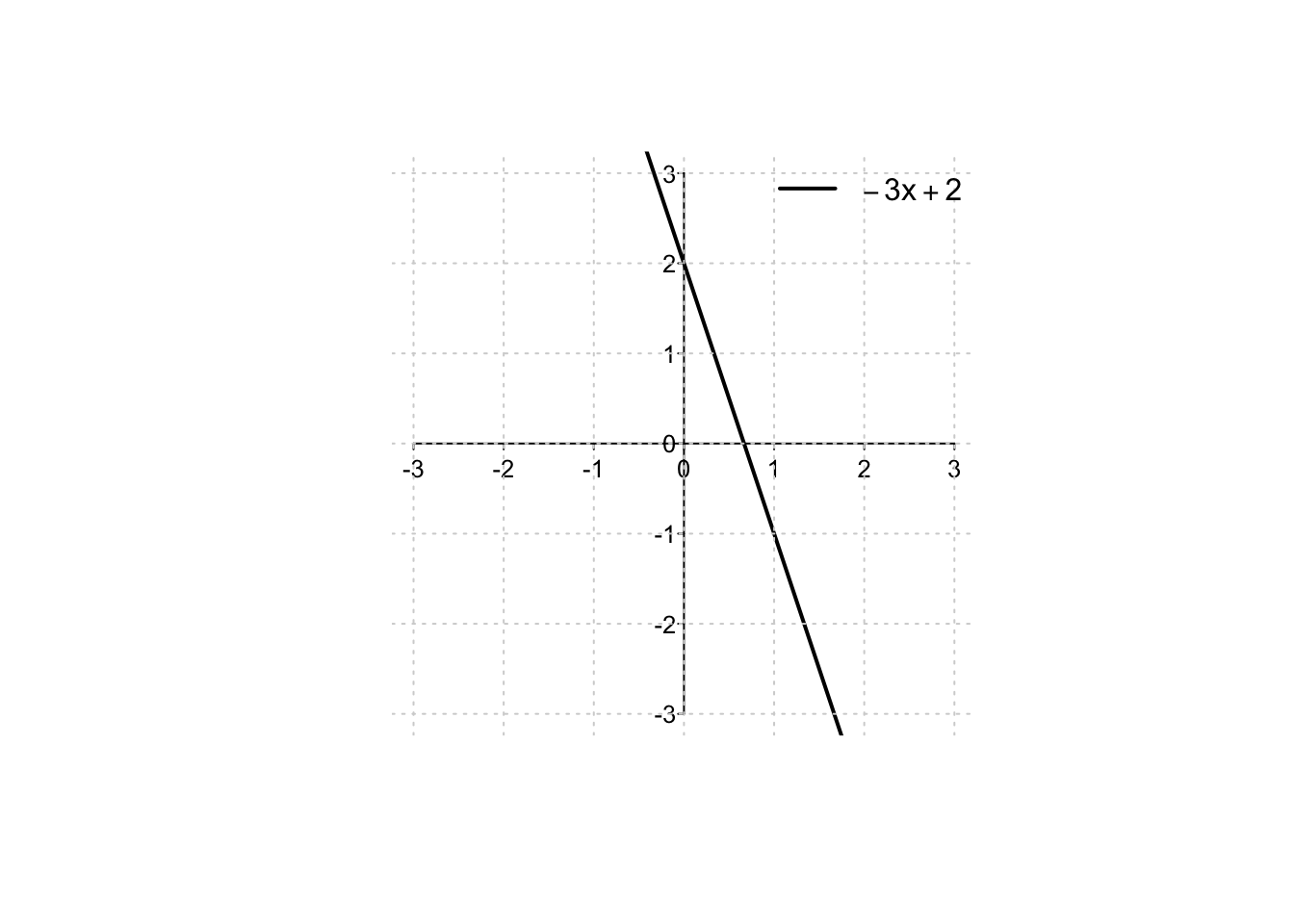 Dal grafico, si deduce anche la soluzione della associata disequazione di primo grado.
La retta assume infatti valori non negativi per valori a sinistra della sua intersezione con l’asse delle ascisse:
\[
-3x+2\geq 0 \;\Rightarrow \; -3x \geq -2 \; \Rightarrow \; 3x \leq 2 ,\; \text{ per }\; x \in (-\infty,2/3].
\]
Dal grafico, si deduce anche la soluzione della associata disequazione di primo grado.
La retta assume infatti valori non negativi per valori a sinistra della sua intersezione con l’asse delle ascisse:
\[
-3x+2\geq 0 \;\Rightarrow \; -3x \geq -2 \; \Rightarrow \; 3x \leq 2 ,\; \text{ per }\; x \in (-\infty,2/3].
\]
Le notazioni \(x \leq 2/3\) e \(x \in (-\infty,2/3]\) sono equivalenti, ma per gli scopi di questo libro suggeriamo di utilizzare la seconda notazione insiemistica, con la quale verranno indicate le soluzioni degli esercizi.
2.2 Funzioni quadratiche
Le funzioni reali del tipo \(f: \mathbb{R} \to \mathbb{R},\) \[ f(x)=ax^2+bx+c, \quad a,b,c \in \mathbb{R},\;a \neq 0, \] sono dette funzioni quadratiche ed hanno come grafico una parabola. Le funzioni quadratiche sono la famiglia più semplice di funzioni che possano essere sia convesse che concave.
Le funzioni quadratiche dipendono da tre parametri. Il parametro \(c=f(0)\) identifica, analogamente alla retta, l’intersezione con l’asse delle ordinate, mentre il parametro più importante è il coefficiente \(a\) del termine \(x^2\) perché regola la convessità della funzione:
se \(a>0\), la parabola è strettamente convessa;
se \(a<0\), la parabola è strettamente concava.
(Se \(a=0\), caso escluso dalla definizione, la funzione quadratica diviene lineare.)
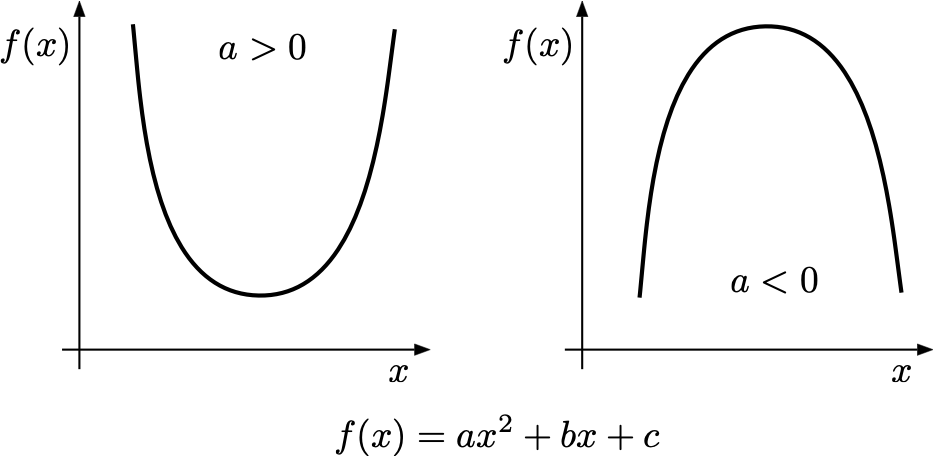
Una funzione quadratica, considerata su tutto l’asse reale, non è né crescente né decrescente e il suo grafico presenta un punto di ordinata più basso/più alto di tutti gli altri, dipendentemente dalla sua convessità/concavità, collocato su quello che viene chiamato il vertice della parabola.
Ricordiamo alcune fondamentali formule per disegnare una parabola e risolvere la corrispondente equazione/disequazione di secondo grado nel seguente esempio.
Example 2.2 Si consideri la funzione \(f:\mathbb{R} \to \mathbb{R},\) \[f(x)= x^2-2x-3.\] Dalla sua forma analitica, si deduce che \(f\) è una parabola convessa. Essa avrà il suo vertice nel punto di ascissa \[x_V=-\frac{b}{2a}=\frac{2}{2}=1,\] con ordinata \(f(1)=-4\). Le intersezioni con l’asse delle ascisse sono date dalle eventuali soluzioni reali della associata equazione di secondo grado \[ x^2-2x-3=0, \] che sono ricavabili dalla formula \[ x_{1,2}=\frac{-b \pm \sqrt{b^2-4ac}}{2a}=\frac{2 \pm \sqrt{4+12}}{2}=-1,3. \] Si osservi che se \(x_{1,2}=-1,3\) sono le soluzioni dell’equazione \(x^2-2x-3=0\), allora si potrà scrivere \[ x^2-2x-3=(x+1)(x-3). \]
Con queste informazioni, si procede a disegnare il grafico della parabola.
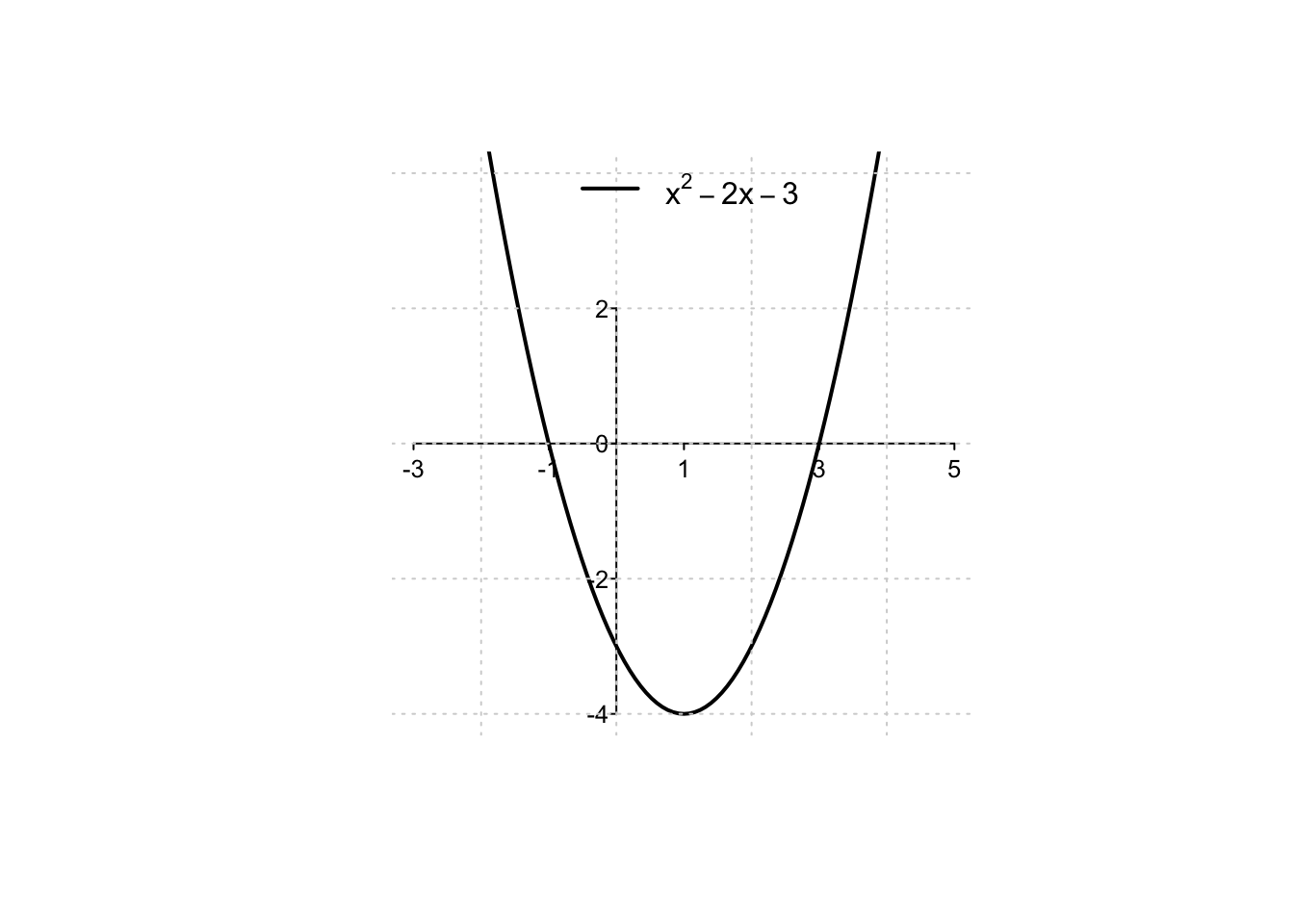 Dalla convessità della parabola, si deduce anche la soluzione della associata disequazione di secondo grado.
La parabola assume infatti valori non negativi per valori esterni alle sue radici:
\[
x^2-2x-3\geq 0, \text{ per } x \in (-\infty, -1] \cup [3,+\infty).
\]
Dalla convessità della parabola, si deduce anche la soluzione della associata disequazione di secondo grado.
La parabola assume infatti valori non negativi per valori esterni alle sue radici:
\[
x^2-2x-3\geq 0, \text{ per } x \in (-\infty, -1] \cup [3,+\infty).
\]
Per risolvere correttamente una disequazione aiuta molto conoscere il grafico delle funzioni coinvolte. Per stabilire se una funzione quadratica assume valori positivi all’interno o all’esterno delle sue eventuali radici, basta sapere se essa descrive una funzione convessa o concava.
2.3 Potenze pari
Si dicono pari le funzioni per le quali il segno della variabile \(x\) non influenza il valore della sua immagine \(f(x)\).
Definition 2.1 Una funzione \(f:\mathbb{R}\to\mathbb{R}\) si dice pari se si ha \[ f(-x)=f(x),\; \text{ per ogni } x \in \mathbb{R}. \]
Per definizione, una funzione pari ha un grafico simmetrico rispetto all’asse delle ordinate.
Il classico esempio di funzioni pari è dato dalla famiglia delle funzioni potenza \(f:\mathbb{R}\to\mathbb{R},\) \[f(x)=x^{2n},\; n \in \mathbb{N},\] con esponente pari (\(2n\)). Tali funzioni, come ad esempio \(f(x)=x^2,x^4,x^6,\dots\), sono funzioni pari e si comportano qualitativamente tutte nello stesso modo:
considerate sull’intero dominio, non sono né crescenti né decrescenti;
sono strettamente convesse;
diventano arbitrariamente grandi se la variabile \(x\) diviene arbitrariamente grande o arbitrariamente piccola;
il loro grafico passa per i punti \((0,0)\), \((1,1)\), e \((-1,1)\);
per \(x>1\) oppure \(x<-1\), si ha \(x^m > x^n\) se \(m>n\);
per \(0<x<1\), si ha \(x^m < x^n\) se \(m>n\).
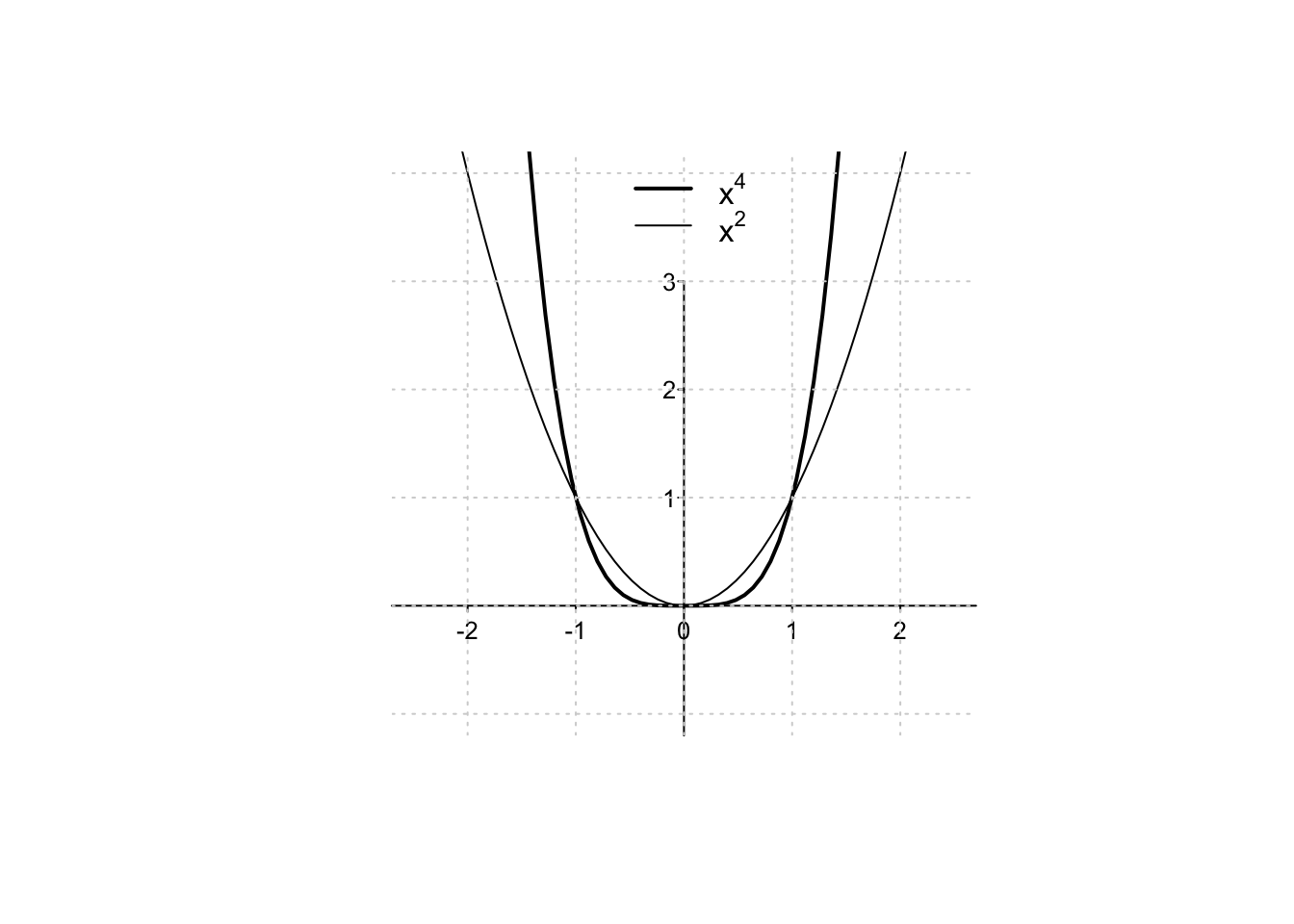
Qualsiasi funzione che dipenda da \(x\) solo tramite potenze pari, è pari. Ad esempio la funzione \(f:\mathbb{R} \to \mathbb{R}, f(x)=x^8-x^2\), è pari.
2.4 Potenze dispari
Si dicono dispari le funzioni \(f(x)\) che cambiano il segno dell’immagine \(f(x)\) se cambia il segno della variabile \(x\).
Definition 2.2 Una funzione \(f:\mathbb{R}\to\mathbb{R}\) si dice dispari se si ha \[ f(-x)=-f(x),\, \text{ per ogni } x \in \mathbb{R}. \]
Per definizione, una funzione dispari ha un grafico simmetrico rispetto all’origine degli assi.
Il classico esempio di funzioni dispari è dato dalla famiglia delle funzioni potenza \(f:\mathbb{R}\to\mathbb{R},\) \[f(x)=x^{2n+1},\; n \in \mathbb{N}_0,\] con esponente dispari (\(2n+1\)). Tali funzioni, come ad esempio \(f(x)=x,x^3,x^5,\dots\), sono dispari e si comportano qualitativamente tutte nello stesso modo:
sono strettamente crescenti;
considerate sull’intero dominio, non sono né convesse né concave (tranne la funzione lineare che è sia convessa che concava);
diventano arbitrariamente grandi se la variabile \(x\) diviene arbitrariamente grande, e arbitrariamente piccole se la variabile \(x\) diviene arbitrariamente piccola;
il loro grafico passa per i punti \((0,0)\), \((1,1)\), e \((-1,-1)\);
per \(x>1\), si ha \(x^m > x^n\) se \(m>n\);
per \(0<x<1\), si ha \(x^m < x^n\) se \(m>n\).
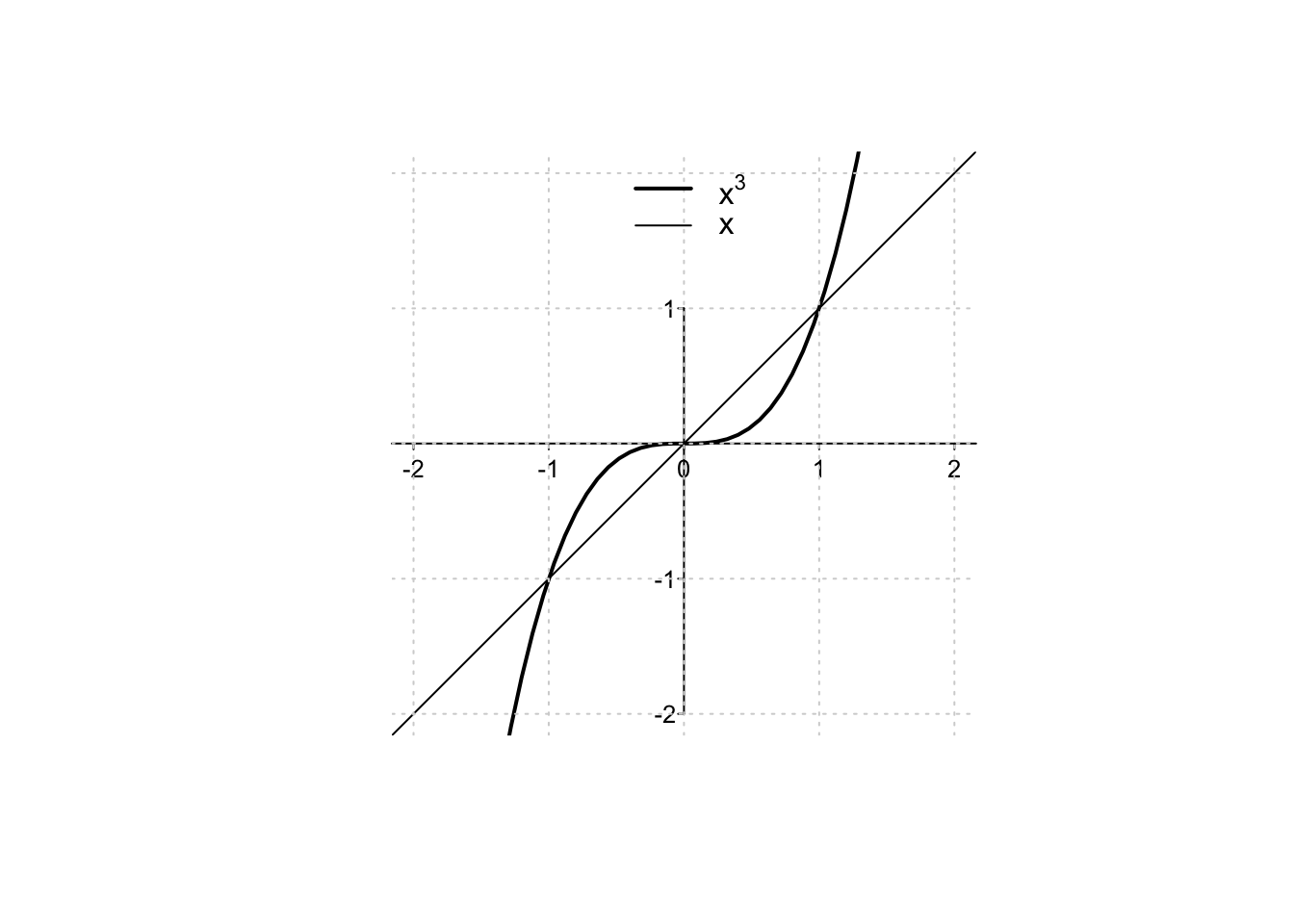
Le definizioni di funzione pari e funzione dispari possono essere estese a funzioni aventi un dominio \(A \subseteq \mathbb{R}\) che sia simmetrico, ovvero tale che \(x \in A \Rightarrow -x \in A\).
Definition 2.3 Una somma algebrica di potenze (pari o dispari) del tipo \[\begin{equation} P(x)=a_nx^n + a_{n-1}x^{n-1}+ \dots + a_1x + a_0, \text{ dove }\; a_0,a_1,\dots,a_n \in \mathbb{R}, \; a_n \neq 0, \tag{2.1} \end{equation}\] è detta polinomio di grado \(n\).
2.5 Valore assoluto
La funzione valore assoluto lascia invariato un numero se esso è positivo, ne cambia il segno se è negativo; ad esempio \(\vert 3 \vert=\vert -3 \vert=3\). Formalmente, la funzione valore assoluto \(f: \mathbb{R}\to \mathbb{R}, f(x)= \vert x\vert\), è definita come \[ \vert x \vert = \begin{cases} \phantom{-}x \quad\text{ se }\, x \geq 0;\\ -x \quad \text{ se }\, x < 0. \end{cases} \] La funzione valore assoluto è pari ed ha un grafico analogo a quello di una potenza pari: non è né crescente né decrescente, ed è convessa (anche se non strettamente).
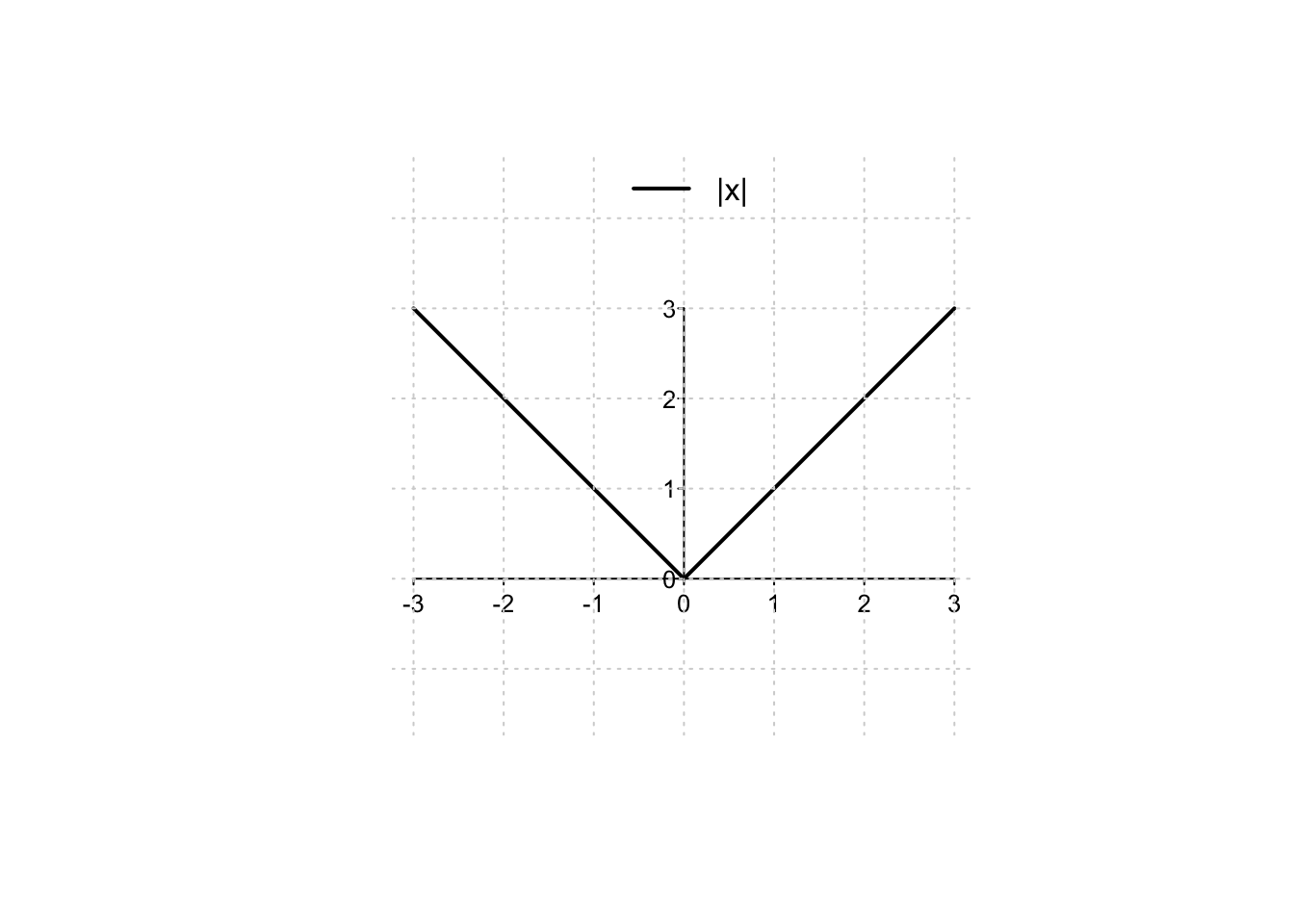
Osservando il grafico del valore assoluto, in corrispondenza di un valore \(k>0\), si possono dedurre le seguenti importanti equivalenze:
\(\vert x \vert =k \quad \Leftrightarrow \quad x=\pm k;\)
\(\vert x \vert \leq k \quad \Leftrightarrow \quad x \in [-k,k]\);
\(\vert x \vert \geq k \quad \Leftrightarrow \quad x \in (-\infty,-k] \cup [k,+\infty)\).
In presenza di una equazione o disequazione con il valore assoluto di una funzione, è necessario procedere discutendo i vari casi separatamente, e quindi unendo le eventuali soluzioni da essi derivanti.
Example 2.3 Si risolva la disequazione \[ \vert x-2 \vert \leq \vert x+3 \vert -x. \] I due valori assoluti danno luogo a tre casi:
CASO I: \(x < -3\); gli argomenti di entrambi i valori assoluti sono negativi e vengono quindi cambiati di segno. Si ha: \[ 2-x \leq -x-3-x \Rightarrow x \leq -5. \] Intersecando questa soluzione con la condizione di esistenza del caso I, si ottiene \[x \in (-\infty,-5].\]
CASO II: \(-3 \leq x < 2\); l’argomento del primo valore assoluto è negativo (e quindi viene cambiato di segno), il secondo rimane immutato. Si ha: \[ 2-x \leq x+3 -x \Rightarrow x \geq -1, \] che, intersecata con la condizione di esistenza del caso II, dà luogo alla soluzione \(x \in [-1,2)\).
CASO III: \(x \geq 2\); gli argomenti di entrambi i valori assoluti sono non negativi e pertanto i valori assoluti possono essere ignorati. Si ha: \[ x-2 \leq x+3 -x \Rightarrow x \leq 5, \] che, intersecata con la condizione di esistenza del caso III, dà luogo alla soluzione \(x \in [2,5]\).
SOLUZIONE FINALE: Unendo le soluzioni dei tre casi si ottiene \(x \in (-\infty,-5] \cup [-1,5].\)
2.6 Funzione inversa
Tutte le funzioni che verranno studiate nel seguito potranno essere costruite a partire dalle funzioni elementari trattate in questo capitolo tramite le operazioni di somma, differenza, prodotto, quoziente, e tramite composizioni.
È immediato estendere le operazioni tra due numeri a operazioni tra due funzioni \(f\) e \(g\), semplicemente eseguendo l’operazione tra i valori delle immagini \(f(x)\) e \(g(x)\). Date due funzioni reali \(f,g:A \to \mathbb{R}\) aventi lo stesso dominio, si definiscono:
la funzione somma \(f+g\), come \((f+g)(x)=f(x)+g(x)\);
la funzione differenza \(f-g\), come \((f-g)(x)=f(x)-g(x)\);
la funzione prodotto \(fg\), come \((fg)(x)=f(x)g(x)\);
la funzione quoziente \(\frac{f}{g}\), come \(\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}\) (in questo caso si deve assumere \(g(x) \neq 0\) per ogni \(x \in A\)).
Si osservi la notazione usata: ad esempio la scrittura \(f+g\) si riferisce alla funzione somma, mentre la scrittura \((f+g)(x)\) identifica l’immagine del numero \(x\) tramite la funzione somma, che per definizione è posta pari a \(f(x)+g(x)\). Quest’ultimo oggetto è un numero reale.
Comporre due funzioni equivale ad applicare al valore \(x\), in successione, prima una funzione \(f\), quindi un’altra funzione \(g\), cioè eseguire: \[ x \to f(x) \to g(f(x)). \]
Definition 2.4 Date due funzioni \(f:A \subseteq \mathbb{R} \to \mathbb{R}\) e \(g: B \to \mathbb{R}\) con \(f(A) \subseteq B\), si dice composizione di \(g\) con \(f\) la funzione \((g \circ f):A \to \mathbb{R}, (g \circ f)(x)=g(f(x))\). In questo caso la funzione \(f\) viene detta funzione interna, la \(g\) funzione esterna.
La composizione è una operazione molto semplice, che illustriamo nel seguente esempio.
Example 2.4 Siano date le due funzioni \[ f:\mathbb{R}\to\mathbb{R},\; f(x)=2x-3, \quad \text{ e } \quad g:\mathbb{R}\to\mathbb{R},\; g(x)=x^2. \] Si ottiene la funzione \((g \circ f)\) come \[ (g \circ f)(x)=g(f(x))=g(2x-3)=(2x-3)^2=4x^2-12x+9. \] Si osservi come la composizione \((f \circ g)\) (ottenuta scambiando la funzione interna con quella esterna) sia differente: \[ (f \circ g)(x)=f(g(x))=f(x^2)= 2x^2-3. \]
Si osservi che non ha nessuna rilevanza la lettera con la quale si identifica la variabile di una funzione. Le due funzioni \(g:\mathbb{R}\to\mathbb{R},\, g(x)=x^2\) e \(f:\mathbb{R}\to\mathbb{R},\, f(t)=t^2\) sono identiche.
Se una funzione \(f:A \subseteq \mathbb{R} \to \mathbb{R}\) è iniettiva, il valore \(f(x)\) potrà essere ottenuto solo a partire da \(x\). Si può pensare allora di definire una nuova funzione che associ al valore \(f(x)\) il valore di partenza \(x\), secondo l’illustrazione seguente. Una tale funzione è detta funzione inversa.
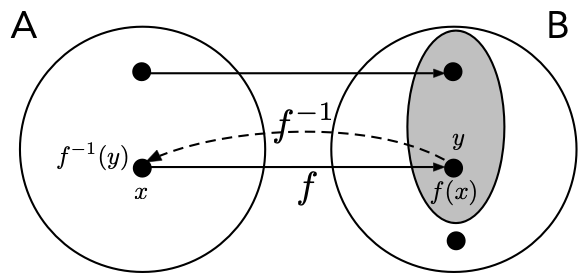
Definition 2.5 Data una funzione iniettiva \(f:A \subseteq \mathbb{R} \to \mathbb{R}\), si dice funzione inversa di \(f\) la funzione \(f^{-1}:\text{Im}(f) \to \mathbb{R}\) definita come \[ f^{-1}(y)=x, \quad \text{con} \quad x: f(x)=y. \]
La funzione inversa soddisfa, per definizione, le seguenti proprietà: \[\begin{equation} \begin{split} f(f^{-1})(y)&=y, \text{ per ogni } y \in \text{Im}(f), \\ f^{-1}(f(x))&=x, \text{ per ogni } x \in A. \end{split} \tag{2.2} \end{equation}\]
2.7 Potenze frazionarie
La definizione di inversa di una funzione ci permette di definire le potenze con esponente frazionario, o radici, attraverso i seguenti esempi.
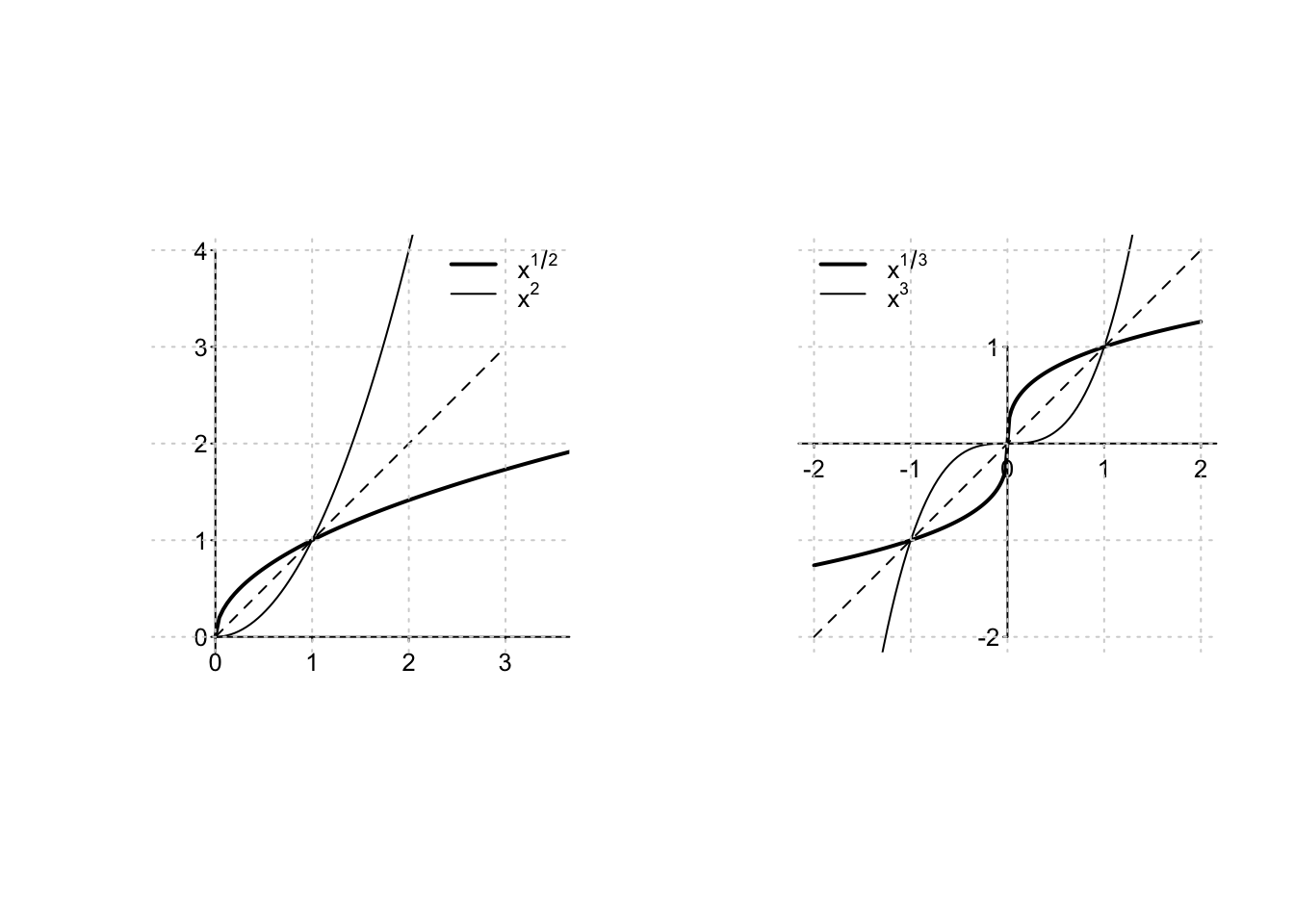
Example 2.5 Si consideri la funzione \(f:\mathbb{R} \to \mathbb{R},\, f(x)=x^2\), che associa ad ogni numero reale il suo quadrato (il numero moltiplicato per se stesso). Essendo una funzione pari, \(f\) non è iniettiva: \(f(1)=f(-1)=1\). Restringendone il dominio al semiasse non negativo, si ottiene la nuova funzione \(g:[0, +\infty) \to \mathbb{R},\, f(x)=x^2\), che è iniettiva e, in quanto tale, possiede funzione inversa \(g^{-1}\). La funzione \(g\) continua ad associare ad ogni numero il proprio quadrato, quindi ha come immagine il semiasse non negativo: \(\text{Im}(g)=[0,+\infty)\). Si avrà dunque che la sua inversa \(g^{-1}:[0,+\infty) \to [0, +\infty)\) assocerà ad ogni numero non negativo quel numero che, elevato alla seconda, lo restituisce. Questa inversa è stata chiamata radice quadrata e l’immagine di \(x\geq0\) viene indicata col simbolo \(\sqrt{x}\), o con la notazione \(x^{1/2}\). Secondo le equazioni (2.2), si ha quindi \[ \sqrt{x^2}=x, \; \left(\sqrt{x}\right)^2=x, \; \text{ per } x \geq 0. \]
Si osservi che le precedenti equazioni valgono per \(x \geq 0\). In generale, per \(x \in \mathbb{R}\), si ha \(\sqrt{x^2}=\vert x \vert\) (per capire la differenza, si provi a sostituire i valori \(3\) e \(-3\)).
È in generale sempre possibile restringere il dominio di una funzione al fine di renderla iniettiva e quindi invertibile. Nell’esempio precedente, avremmo potuto alternativamente considerare la funzione \(h:(-\infty,0] \to \mathbb{R},\, f(x)=x^2\) che possiede una funzione inversa differente da quella che viene comunemente identificata come radice quadrata di un numero (non negativo).
Example 2.6 Si consideri la funzione \(f:\mathbb{R} \to \mathbb{R},\, f(x)=x^3\), che associa ad ogni numero reale il suo cubo (il numero moltiplicato per se stesso per tre volte). Essendo una funzione strettamente crescente, \(f\) è iniettiva e quindi possiede l’inversa \(g^{-1}:\mathbb{R} \to \mathbb{R}\) che associa ad ogni numero reale quel numero che, elevato alla terza, lo restituisce. Questa inversa è stata chiamata radice cubica e l’immagine di \(x\in\mathbb{R}\) viene indicata col simbolo \(\sqrt[3]{x}\), o con la notazione \(x^{1/3}\). Secondo le (2.2), si ha quindi \[ \sqrt[3]{x^3}=x, \; \left(\sqrt[3]{x}\right)^3=x, \; \text{ per } x \in \mathbb{R}. \]
È possibile generalizzare i due esempi appena visti per definire qualsiasi potenza frazionaria del tipo \(x^q, q \in \mathbb{Q}\), per \(x \geq 0\). In pratica, si definisce la \(n\)-ma radice \(x^{\frac{1}{n}}\) di un numero come la funzione inversa di \(x^n, x\geq 0\). Quindi si pone \[x^{\frac{m}{n}}=\left(x^{\frac{1}{n}}\right)^m.\] Infine, si passa a esponenti negativi, per \(x>0\), tramite \[x^{-\frac{m}{n}}=\frac{1}{\left(x^{\frac{1}{n}}\right)^m}.\] Nel seguito faremo uso solo della radice quadrata \(\sqrt{x}=x^{\frac{1}{2}}\) (definita su \([0, +\infty)\)) e della radice cubica \(\sqrt[3]{x}=x^{\frac{1}{3}}\) (definita su tutto \(\mathbb{R}\)) di un numero, anche se le formule e le regole che enunceremo per le potenze valgono con maggiore generalità.
Quando si calcola una funzione inversa, in pratica si scambiano le coordinate del punto \((x,y=f(x))\) del grafico di \(f(x)\). Per questo motivo, il grafico di una funzione e della sua inversa sono simmetrici rispetto alla bisettrice degli assi \(y=x\). Da questa proprietà discendono i grafici delle potenze frazionarie \(x^{1/2}\) e \(x^{1/3}\): essi rappresentano funzioni strettamente crescenti e, per \(x \geq 0\), funzioni concave: sono due funzioni quindi che crescono più lentamente delle funzioni quadrato e cubo.
Dagli esempi precedenti e dalla definizione di funzione inversa, si deduce facilmente il seguente risultato.
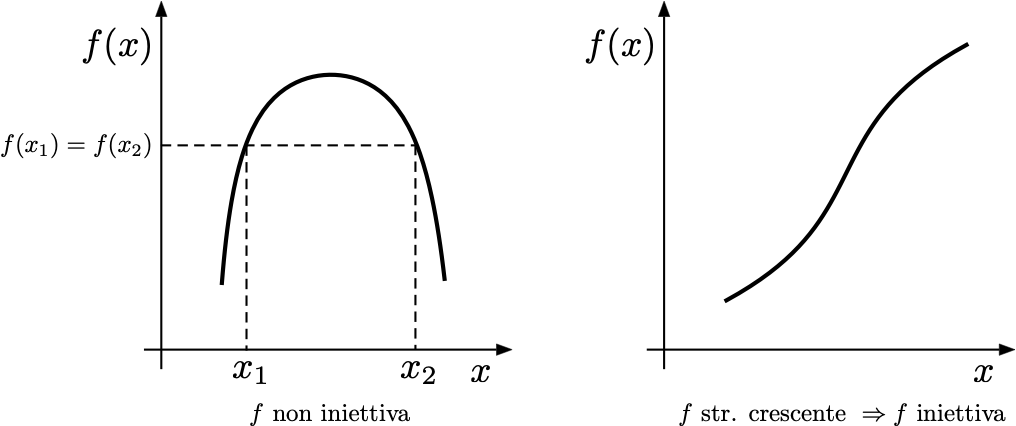
Theorem 2.1 Una funzione \(f:\mathbb{R} \to \mathbb{R}\) strettamente crescente o strettamente decrescente è iniettiva, quindi possiede inversa.
Proof. Se \(f\) non fosse iniettiva, esisterebbero due numeri reali \(x_1<x_2\) tali che \(f(x_1)=f(x_2)\), quindi essa non potrebbe essere strettamente crescente o strettamente decrescente.
L’introduzione delle potenze frazionarie ci permette di ripassare il metodo di risoluzione delle disequazioni illustrate nei seguenti due esempi. È molto importante saper gestire correttamente l’utilizzo delle proprietà di monotonia illustrate sino a questo punto.
Example 2.7 Si risolva la disequazione \[ \sqrt[3]{x^3-2x+2}-x+2>0. \] La risoluzione di disequazioni dove compare la radice cubica non dà in generale grossi problemi. In questo caso, isolando la radice a sinistra si ottiene: \[ \sqrt[3]{x^3-2x+2}>x-2. \] A questo punto, essendo la funzione \(f:\mathbb{R}\to\mathbb{R},\,f(x)=x^3\) strettamente crescente, applicandola ad entrambi i membri della disequazione, ne manterrà il verso: \[ \left(\sqrt[3]{x^3-2x+2}\right)^3>(x-2)^3. \] Applicando le proprietà (2.2) dell’inversa, e svolgendo il cubo a destra, si ottiene \[ x^3-2x+2>x^3-6x^2+12x-8, \] da cui si ottiene \[\begin{align*} 6x^2-14x+10>0, \\ 3x^2-7x+5>0, \end{align*}\] che è (\(a=3>0\), \(b^2-4ac=-11<0\)) sempre soddisfatta, per ogni \(x \in \mathbb{R}\).
Example 2.8 Si risolva la disequazione \[ \sqrt{x^2-2x-1}-x+2>0 \] La risoluzione di disequazioni dove compare la radice quadrata deve essere trattata con cura. Prima di tutto, l’argomento della radice deve essere non negativo, quindi si porrà dal principio \[ x^2-2x-1 \geq 0, \] che ha come soluzioni \(x \in (-\infty,1-\sqrt{2}] \cup [1+\sqrt{2}, +\infty)\). Qualsiasi soluzione trovata di seguito dovrà essere intersecata con questo insieme di esistenza della radice.
A questo punto, isolando la radice a sinistra si ottiene: \[\begin{equation} \sqrt{x^2-2x-1}>x-2. \tag{2.3} \end{equation}\] Dato che la funzione \(f:\mathbb{R}\to\mathbb{R},\,f(x)=x^2\) non è crescente, non è possibile applicarla ad entrambi i membri della disequazione. Dobbiamo quindi distinguere due casi e risolverli singolarmente, unendone poi le soluzioni.
CASO I: \(x-2<0\); se \(x<2\), il membro di destra della (2.3) è negativo, mentre una radice quadrata (quando esiste) è sempre non negativa. In questo caso, la disequazione è sempre soddisfatta. Intersecando con l’insieme di esistenza delle soluzioni da questo caso si ottiene \(x \in (-\infty,1-\sqrt{2}]\).
CASO II: \(x-2 \geq 0\); se \(x\geq2\), tutti e due i membri della (2.3) sono non negativi. Applicando la funzione \(g:[0,+\infty)\to\mathbb{R},\,f(x)=x^2\), che è strettamente crescente, ad entrambi i membri della disequazione, se ne manterrà il verso: \[ \left(\sqrt{x^2-2x-1}\right)^2>(x-2)^2. \] Applicando le proprietà (2.2) dell’inversa, e svolgendo il quadrato a destra, si ottiene \[ x^2-2x-1>x^2-4x+4, \] quindi: \[ 2x>5 \Rightarrow x>5/2. \] Intersecando con l’insieme di esistenza delle soluzioni da questo caso si ottiene \(x \in (5/2,+\infty)\).
Unendo le soluzioni del caso I e del caso II, si ottiene la soluzione finale: \[ x \in (-\infty,1-\sqrt{2}] \cup (5/2,+\infty). \]
2.8 Logaritmo ed esponenziale
Introduciamo le ultime due funzioni elementari che serviranno nel seguito: la funzione logaritmo e, come sua funzione inversa, la funzione esponenziale.
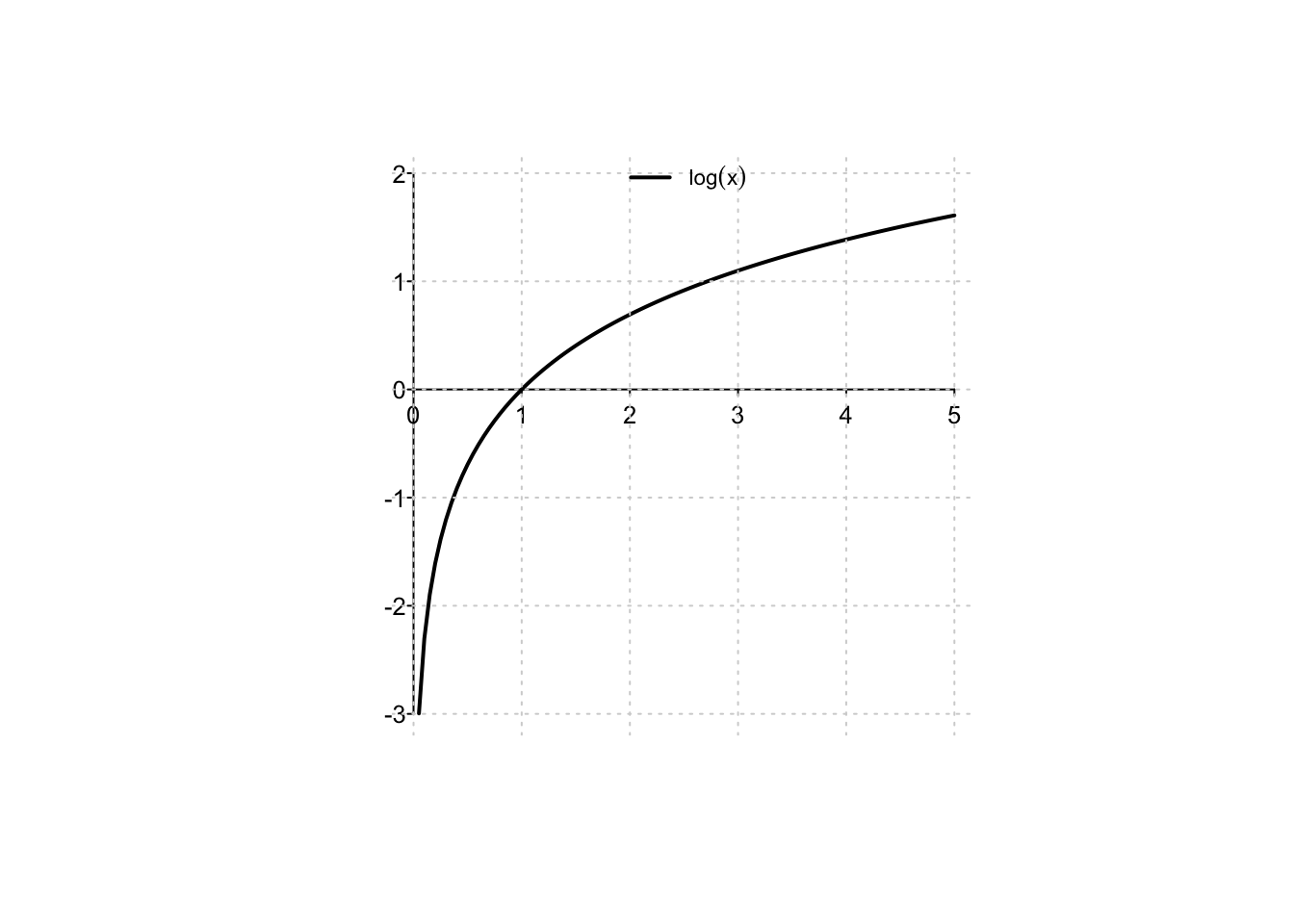
Definition 2.6 Sia \(f:(0,+\infty) \to \mathbb{R}, f(x)=\log(x)\), definita come:
\(\log(x)\) è il valore dell’area compresa sopra l’asse delle ascisse e sotto il grafico della funzione \(\frac{1}{x}\), tra i punti \(1\) e \(x\), se \(x > 1\) (figura a sinistra);
\(\log(x)\) è il valore negativo dell’area compresa sopra l’asse delle ascisse e sotto il grafico della funzione \(\frac{1}{x}\), tra i punti \(x\) e \(1\), se \(x < 1\) (figura a destra);
\(\log(1)=0\).

Confrontando le aree, è immediato verificare che la funzione logaritmo è strettamente cre-scente e, nel seguito, dimostreremo le seguenti proprietà che vengono evidenziate dal suo grafico:
per valori di \(x\) positivi prossimi allo zero, il logaritmo assume valori arbitrariamente piccoli;
all’aumentare di \(x\), il logaritmo assume valori arbitrariamente grandi;
è una funzione strettamente crescente e strettamente concava.
Nel linguaggio comune, l’essere “arbitrariamente piccoli” di solito è associato al fatto di essere vicini a zero. Nel linguaggio matematico essere “arbitrariamente piccoli” significa assumere valori in un intorno di \(-\infty\), quindi negativi e arbitrariamente grandi in valore assoluto.
Inoltre, valgono le seguenti proprietà del logaritmo:
- il logaritmo di un prodotto è la somma dei logaritmi: \[\log(xy)=\log(x) + \log(y), \text{ per } x,y >0;\]
Questa proprietà è il motivo storico dell’introduzione del logaritmo, che avvenne ad opera di John Napier (Nepero) nel 1614. Il logaritmo venne introdotto per facilitare il calcolo del prodotto di fattori molto grandi, che poteva essere così ridotto ad una somma (dei loro logaritmi). Può apparire scontato oggi, ma grazie al logaritmo fu possibile ad esempio formulare le leggi del moto planetario (Keplero). Ecco perché il volume in cui furono introdotti venne intitolato: Mirifici logarithmorum canonis descriptio, ovvero Descrizione della meravigliosa regola dei logaritmi.
- il logaritmo della \(n\)-ma potenza di \(x\) è \(n\) volte il logaritmo di \(x\): \[\log(x^n)=n \log(x) \text{ per } x>0,\, n \in \mathbb{N}. \]
In questo testo, con la notazione \(\log (x)\) indichiamo quello che comunemente è detto logaritmo naturale o logaritmo in base e. Se si utilizza un logaritmo in base \(a\), \(a>0\), ci si può sempre ricondurre al logaritmo naturale tramite la formula \[ \log_a (x) =\frac{\log (x)}{\log (a)}. \] Testi o linguaggi di programmazione diversi usano notazioni differenti per la funzione logaritmo (la più comune è \(\ln\)). Nel seguito useremo esclusivamente \(\log\).
Essendo una funzione strettamente crescente, il logaritmo ammette funzione inversa, detta funzione esponenziale. Essa ha come dominio l’immagine del logaritmo, ovvero tutto l’asse reale, e come immagine il dominio del logaritmo, ovvero potrà assumere solo valori positivi.
Definition 2.7 La funzione esponenziale \(f: \mathbb{R} \to (0,+\infty), f(x)=\exp(x)=e^x\) è la funzione inversa della funzione logaritmo e, in quanto tale, soddisfa \[\begin{align*} e^{\log(x)}&=x, \text{ per ogni } x>0;\\ \log\left( e^x\right)&=x, \text{ per ogni } x\in\mathbb{R}. \end{align*}\]
Essendo la funzione inversa del logaritmo, il grafico della funzione esponenziale è simmetrico rispetto a quello del logaritmo rispetto alla bisettrice degli assi \(y=x\). Questo implica le seguenti proprietà:
al diminuire di \(x\), la funzione esponenziale assume valori prossimi allo zero; all’aumentare di \(x\), assume valori arbitrariamente grandi;
la funzione esponenziale è sempre definita, positiva, strettamente crescente e strettamente convessa.
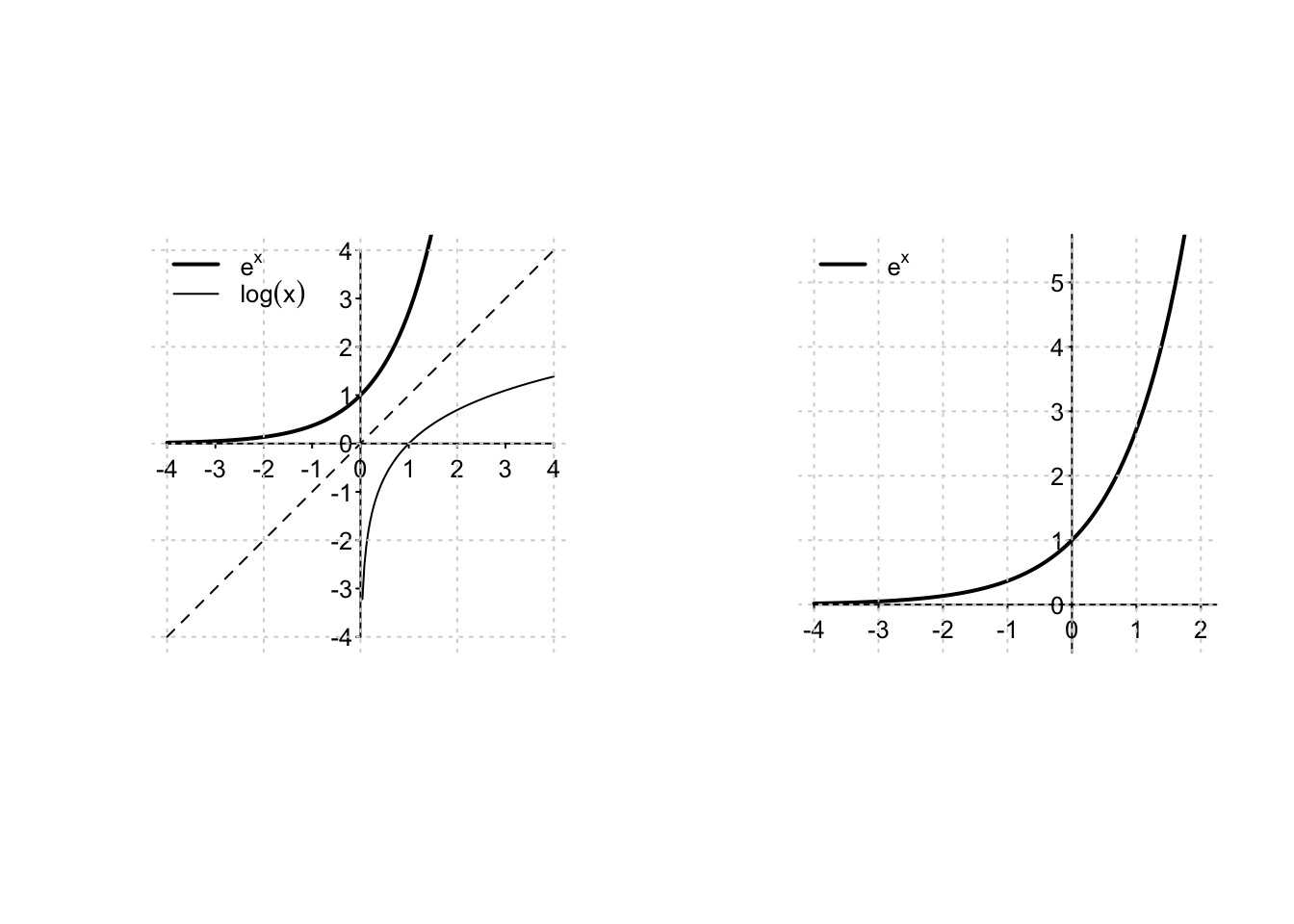
Si osservi che, essendo l’esponenziale definita come l’inversa della funzione logaritmo, tutte le sue proprietà e il suo comportamento derivano per simmetria da quelli del logaritmo. È possibile ribaltare questa prospettiva definendo prima la funzione esponenziale, e quindi il logaritmo come sua inversa. Nel seguire quest’ultimo approccio, si deve prestare particolare attenzione a fornire una definizione formalmente corretta di funzione esponenziale.
Essendo la funzione inversa del logaritmo, per l’esponenziale valgono le seguenti proprietà:
\(e^0= 1\) (poiché \(\log(1)=0\));
l’esponenziale della somma è il prodotto delle esponenziali: \[e^{x+y}=e^xe^y, \,\text{ per }\, x,y \in \mathbb{R};\]
l’esponenziale del prodotto è la potenza dell’esponenziale: \[e^{nx}=(e^x)^n\,\text{ per }\, x\in \mathbb{R},\, n \in \mathbb{N}.\]
È stato dimostrato che il numero \(e^1=e\) non è solo un numero irrazionale (quindi non esprimibile sotto forma di frazione), ma è anche trascendente; in particolare, rimane irrazionale anche se elevato a qualsiasi potenza intera (si noti la differenza con \(\sqrt{2}\) per cui si ha \((\sqrt{2})^2=2\)).
I successivi esempi illustrano la risoluzione di disequazioni esponenziali e logaritmiche.
Example 2.9 Si risolva la disequazione \[ e^{-x^2+2} \leq e^{x}. \] Essendo la funzione esponenziale strettamente crescente, essa conserva l’ordinamento dei suoi argomenti, quindi la disequazione risulta equivalente a \[ -x^2+2 \leq x. \] Si deve quindi risolvere la disequazione di secondo grado \(-x^2-x+2 \leq 0\), che ha come soluzione \(x \in (-\infty,-2] \cup [1, +\infty)\).
Example 2.10 Si risolva la disequazione \[ \log(-x^2+2) \leq \log(x). \] Prima di tutto, è necessario discutere l’esistenza dei logaritmi presenti, ovvero richiedere che i rispettivi argomenti siano positivi: \[ -x^2+2 > 0, \quad x>0, \quad \text{ ovvero } x^2< 2, \quad x>0. \] L’intersezione delle soluzioni di queste due disequazioni è data dall’insieme di esistenza: \[ x \in (0, \sqrt{2}). \] Solo a questo punto, dopo aver discusso l’esistenza dei logaritmi, si può procedere analogamente all’esercizio precedente. Essendo la funzione logaritmo strettamente crescente, essa conserva l’ordinamento dei suoi argomenti, quindi la disequazione risulta equivalente (sul suo campo di esistenza) a \[ -x^2+2 \leq x. \] Si deve quindi risolvere la disequazione di secondo grado \(-x^2-x+2 \leq 0\), che ha come soluzione \(x \in (-\infty,-2] \cup [1, +\infty)\). Tale soluzione va intersecata con il campo di esistenza della disequazione originaria, ottenendo come soluzione finale \[ x \in [1, \sqrt{2}). \]
Example 2.11 Si risolva la disequazione \[\begin{equation} e^{-x^2+2} < 2. \tag{2.4} \end{equation}\] In questi casi è possibile sfruttare il fatto che l’esponenziale è l’inversa del logaritmo, e quindi applicare il logaritmo a sinistra e a destra di \(<\), ottenendo: \[ -x^2+2 < \log 2. \] Si osservi che questa operazione è possibile in quanto entrambi i membri della disequazione (2.4) sono positivi, quindi il loro logaritmo è ben definito (se a destra ci fosse stato \(-2\), si può immediatamente verificare che la disequazione \(e^{-x^2+2} < -2\) non sarebbe stata soddisfatta per nessun valore di \(x\)). La disequazione risultante \[ x^2>2-\log2 \] è risolta per \(x \in (-\infty,-\sqrt{2-\log 2}) \cup (\sqrt{2-\log 2}, +\infty)\).
Un comune (purtroppo) e grave errore è scrivere come soluzione della disequazione \(x^2 \geq c\), per \(c \geq 0\), l’insieme dei numeri reali \(x \geq \pm \sqrt{c}\), notazione priva di senso e, in ogni sua interpretazione, errata. La disequazione \(x^2 \geq c\), per \(c > 0\), è risolta per \(x \in (-\infty, -\sqrt{c} \,] \cup [\sqrt{c}, +\infty)\); per \(c \leq 0\), è sempre soddisfatta.
Example 2.12 Si risolva la disequazione \[ \log(x-3) < 1. \] Prima di tutto, la discussione dell’esistenza del logaritmo implica che ogni eventuale soluzione debba appartenere all’insieme di esistenza \[ x-3 >0 \,\Rightarrow\, x>3. \] Quindi, analogamente all’esempio precedente, si può applicare l’esponenziale ad entrambi i membri della disequazione, ottenendo \[ e^{\log(x-3)}< e, \] ovvero \[ x-3<e \,\Rightarrow\, x<3+e. \] Intersecando con l’insieme di esistenza, si ottiene come soluzione finale \[ x \in (3,3+e). \]
In conclusione, in presenza di una disequazione logaritmica/esponenziale, si può sempre provare ad eliminare la funzione logaritmica/esponenziale applicando la sua inversa, dopo aver precedentemente discusso l’esistenza degli eventuali logaritmi presenti (l’esponenziale è sempre ben definita).
Mentre è sempre possibile risolvere analiticamente una (dis)equazione di primo o se-condo grado, non tutte le (dis)equazioni logaritmiche/esponenziali hanno una soluzione che può essere scritta analiticamente in forma chiusa. Ad esempio, la disequazione \[ e^{-x^2} > x \] è risolvibile solo numericamente.
2.9 Dominio naturale
Una funzione è un oggetto matematico definito da un dominio, un codominio, e una corrispondenza che per le funzioni reali può essere espressa mediante una formula analitica, come ad esempio per la funzione quadrato \(f:\mathbb{R} \to \mathbb{R}, \, f(x)=x^2\).
Nel seguito, espliciteremo una funzione esclusivamente attraverso la sua formula analiti-ca, sottintendendo come codominio tutta la retta reale e come dominio il più grande sottoinsieme della retta reale in cui è possibile definire la funzione.
Definition 2.8 Per una funzione \(f:D_f \subseteq \mathbb{R}\to \mathbb{R}\) definita dall’espressione analitica \(x \to f(x)\), l’insieme \(D_f\) è detto dominio naturale di \(f\) se esso è il più grande sottoinsieme di \(\mathbb{R}\) in cui \(f(x)\) è correttamente definita.
Con le funzioni introdotte ed usate in questo testo, un restringimento del dominio naturale di una funzione rispetto a tutta la retta reale \(\mathbb{R}\) può essere causato da:
la presenza di una frazione, in cui il denominatore deve essere non nullo: \[ \frac{f(x)}{g(x)}, \quad g(x)\neq 0; \]
la presenza di una radice quadrata, il cui argomento deve essere non negativo: \[ \sqrt{f(x)}, \quad f(x) \geq 0; \]
la presenza di un logaritmo, il cui argomento deve essere positivo: \[ \log(f(x)), \quad f(x) > 0. \]
Example 2.13 Si calcoli il dominio naturale della funzione \(f:D_f \to \mathbb{R},\) definita come \[ f(x)=\sqrt{\log\left(\frac{x}{x^2-1}\right)}. \] In questa funzione compaiono tutte le funzioni elementari studiate che possono dare luogo ad un restringimento del dominio naturale rispetto a tutta la retta reale. Si hanno i seguenti vincoli:
\[\begin{align*} \begin{cases} \log\left(\frac{x}{x^2-1}\right) \geq 0 &\text{ (l'argomento della radice quadrata deve essere non negativo)},\\ \frac{x}{x^2-1}>0 &\text{ (l'argomento del logaritmo deve essere positivo),}\\ x^2-1 \neq 0 &\text{ (il denominatore della frazione deve essere non nullo).} \end{cases} \end{align*}\]
Si osservi come il primo vincolo sia più stringente del secondo. Un logaritmo è infatti non negativo se il suo argomento è maggiore o uguale ad uno: \[ \log\left(\frac{x}{x^2-1}\right) \geq 0 \;\Rightarrow\; \frac{x}{x^2-1}\geq 1. \] Il dominio naturale \(D_f\) è quindi dato dalla intersezione delle soluzioni di: \[\begin{align*} \begin{cases} \frac{x}{x^2-1} \geq 1, \\ x^2-1 \neq 0. \end{cases} \end{align*}\]
Per risolvere la prima disequazione è necessario scriverla come \[ \frac{x}{x^2-1}-1 \geq 0, \] quindi \[ \frac{-x^2+x+1}{x^2-1} \geq 0. \] A questo punto si studiano separatamente il segno di numeratore e denominatore del membro di sinistra.
Il NUMERATORE, essendo una parabola concava, assume valori non negativi all’interno delle sue radici: \(-x^2+x+1\geq 0\), per \(x \in [\frac{1-\sqrt{5}}{2},\frac{1+\sqrt{5}}{2}]\).
Il DENOMINATORE, essendo una parabola convessa, assume valori positivi (dobbiamo eliminare i punti \(x=-1,1\) che lo annullano) all’esterno delle sue radici: \(x^2-1 > 0\), per \(x \in (-\infty,-1) \cup (1,+\infty)\).
Lo studio finale del segno ha come soluzione il dominio naturale:
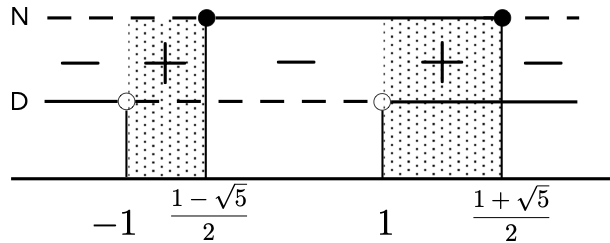 \[
D_f=\left(-1,\frac{1-\sqrt{5}}{2}\right] \cup \left(1,\frac{1+\sqrt{5}}{2}\right].
\]
\[
D_f=\left(-1,\frac{1-\sqrt{5}}{2}\right] \cup \left(1,\frac{1+\sqrt{5}}{2}\right].
\]
Nel risolvere studi del segno come quello dell’esempio appena concluso, è necessario saper ordinare correttamente i numeri reali senza utilizzare un calcolatore. Questo può generare errori soprattutto quando si ha a che fare con numeri negativi. Ad esempio, nell’esempio precedente, è necessario riconoscere che \[ \frac{1-\sqrt{5}}{2} >-1, \] che è equivalente a scrivere \[ 1-\sqrt{5}>-2 \;\Rightarrow\; \sqrt{5}<3 \;\Rightarrow\; 5<3^2=9. \]
È un grave errore risolvere la disequazione \[ \frac{x}{x^2-1}\geq 1 \] studiando le due disequazioni \(x\geq 1\) e \(x^2-1 \geq 1\). Si può operare uno studio sensato del segno solo quando a destra del verso di disequazione compare lo 0, come nell’esercizio precedente: \[ \frac{-x^2+x+1}{x^2-1} \geq 0. \]
2.10 Grafici di funzioni
Conoscendo il grafico delle funzioni elementari, può essere facilmente ricavato il grafico di funzioni leggermente più complesse, ottenute dalle prime mediante semplici operazioni. Data la funzione \(f: A \subseteq \mathbb{R} \to \mathbb{R}\), \(x \to f(x)\), si hanno ad esempio i seguenti casi:
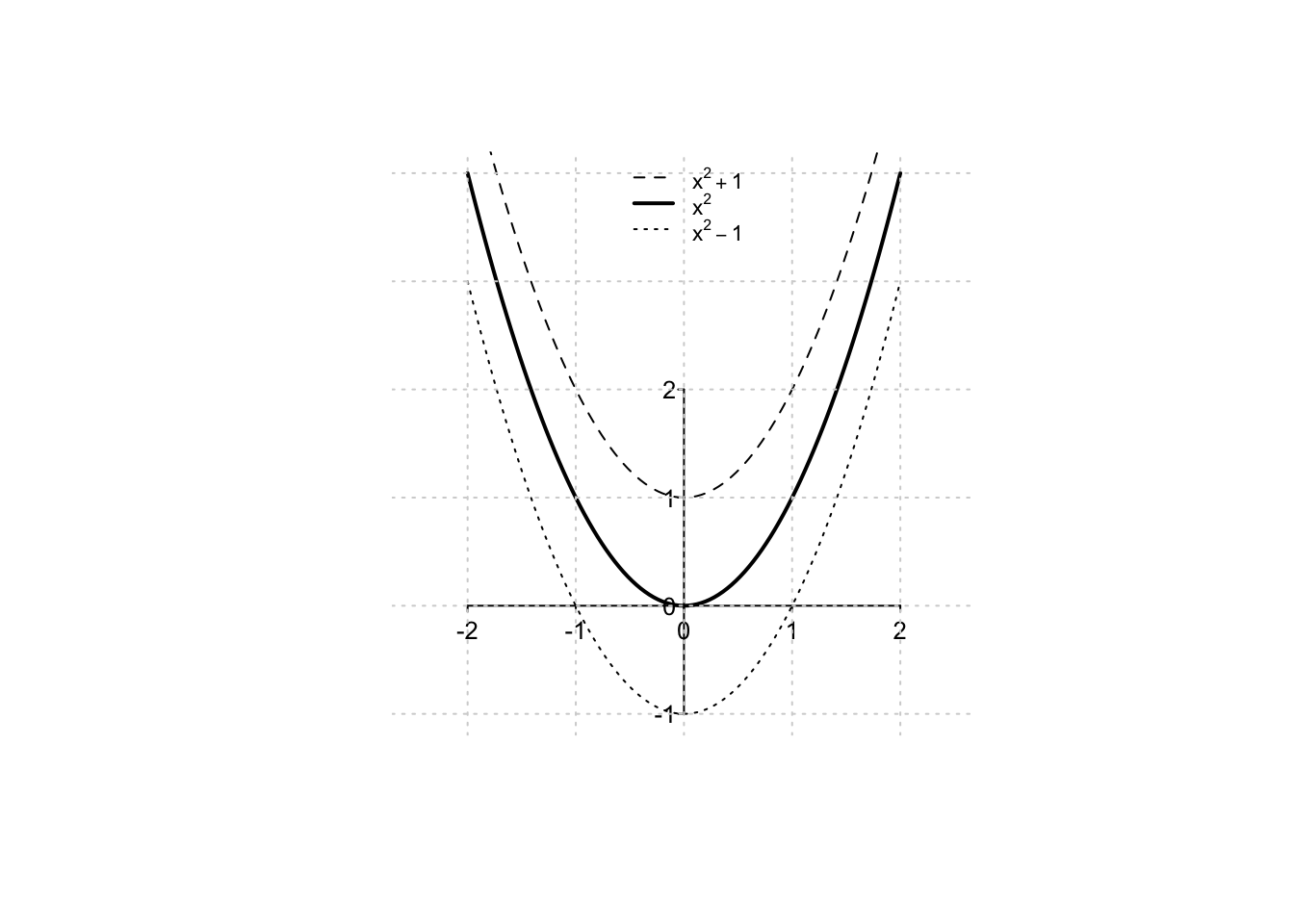
- \(f(x)+k\); se ad una funzione viene sommata una costante \(k\in \mathbb{R}\), il suo grafico risulterà traslato verso l’alto se \(k > 0\); verso il basso se \(k < 0\);
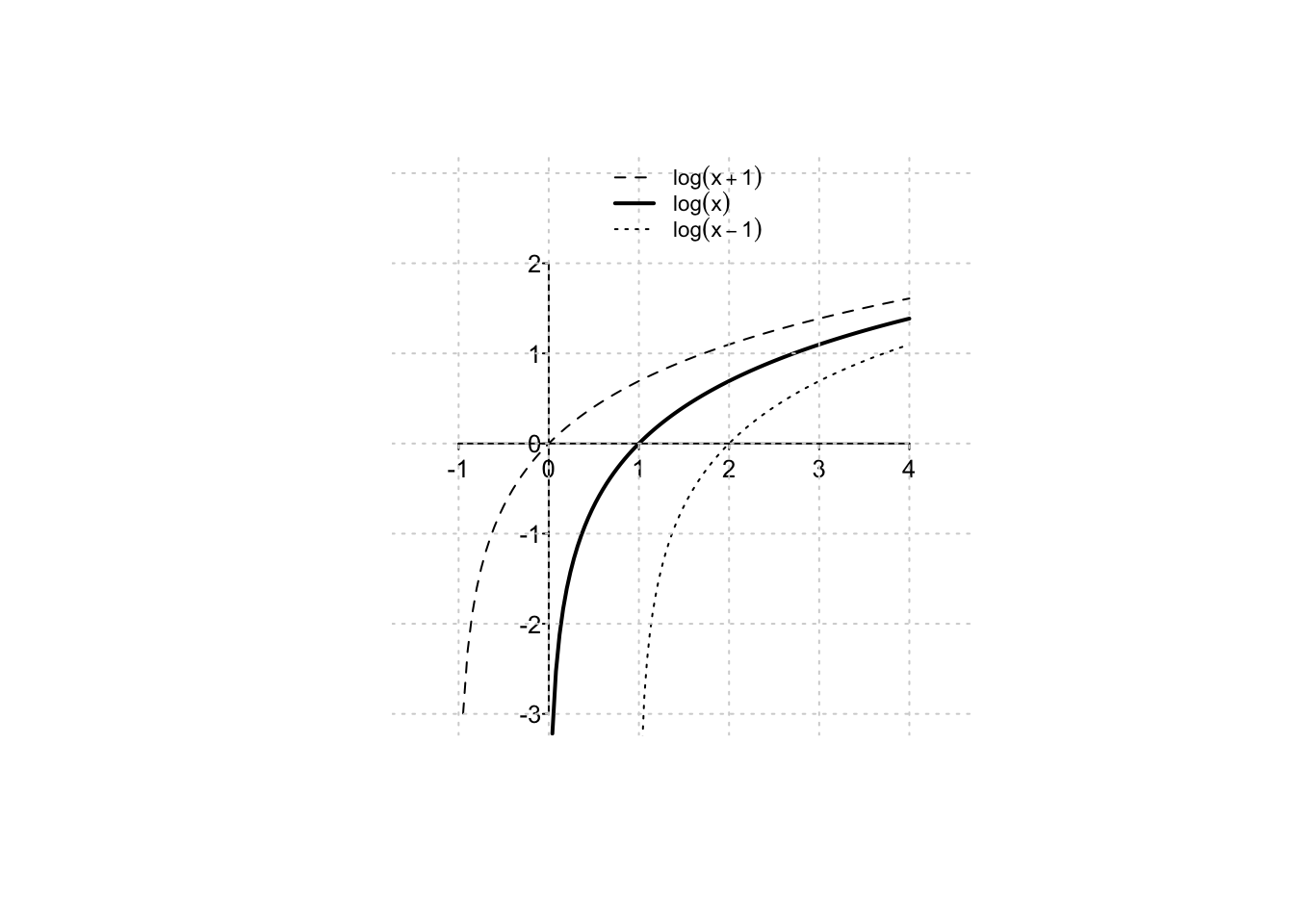
- \(f(x+k)\); se alla variabile di una funzione viene sommata una costante \(k\in \mathbb{R}\), il suo grafico risulterà traslato verso sinistra se \(k > 0\); verso destra se \(k< 0\);
- \(\vert f(x) \vert\); il valore assoluto, se applicato ad una funzione, lascerà invariata la parte non negativa, ribaltando rispetto all’asse delle ascisse la parte negativa;
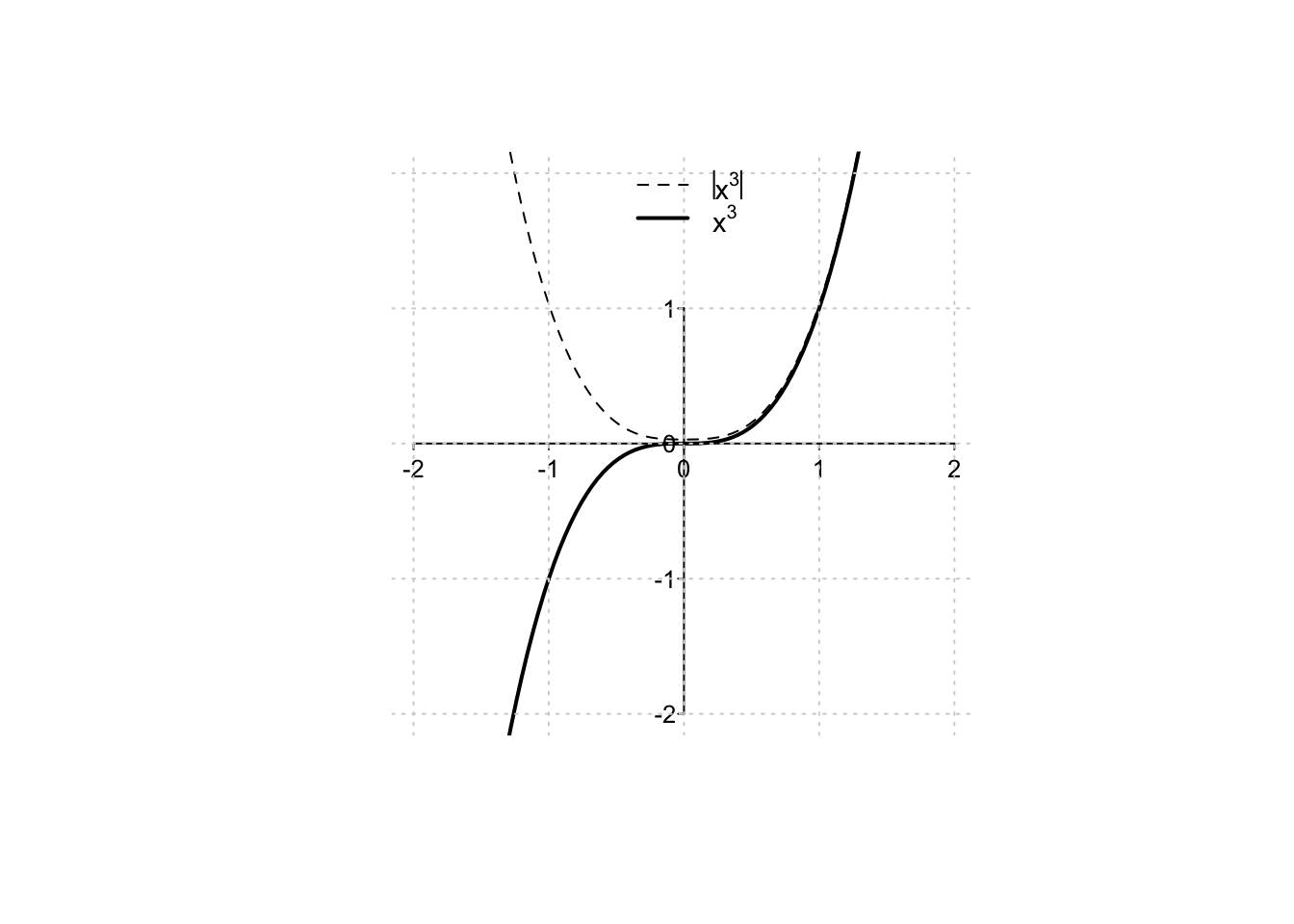
- \(f(\vert x \vert)\); il valore assoluto, se applicato alla variabile di una funzione, la renderà una funzione pari. Il grafico della funzione risultante sarà dunque simmetrico rispetto all’asse delle ordinate.
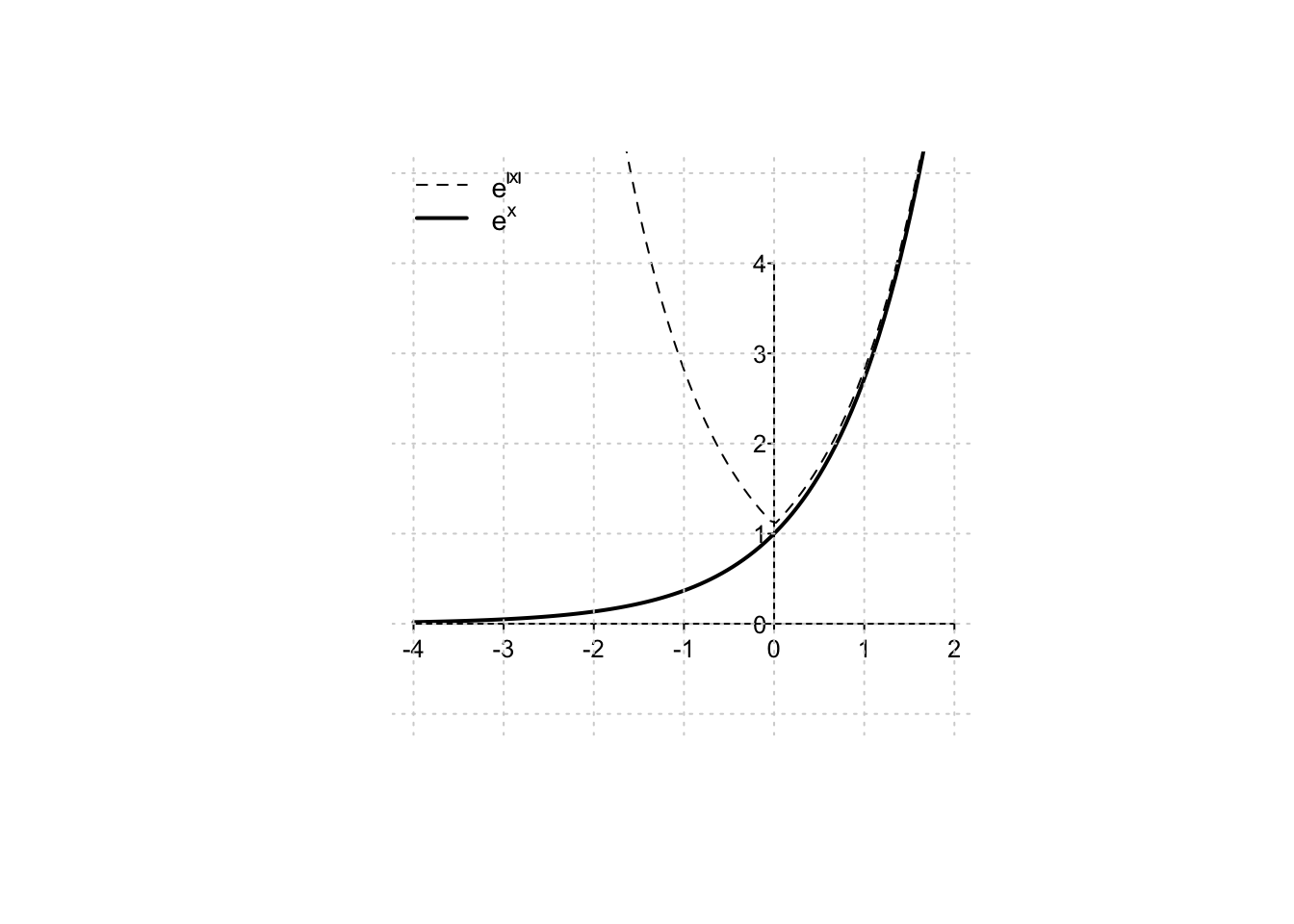
Saper disegnare il grafico delle funzioni elementari, e di loro semplici composizioni, permette di identificare immediatamente sull’asse delle \(x\) il dominio naturale di una funzione, e sull’asse \(y\) la sua immagine (l’insieme dei valori da essa raggiunti).
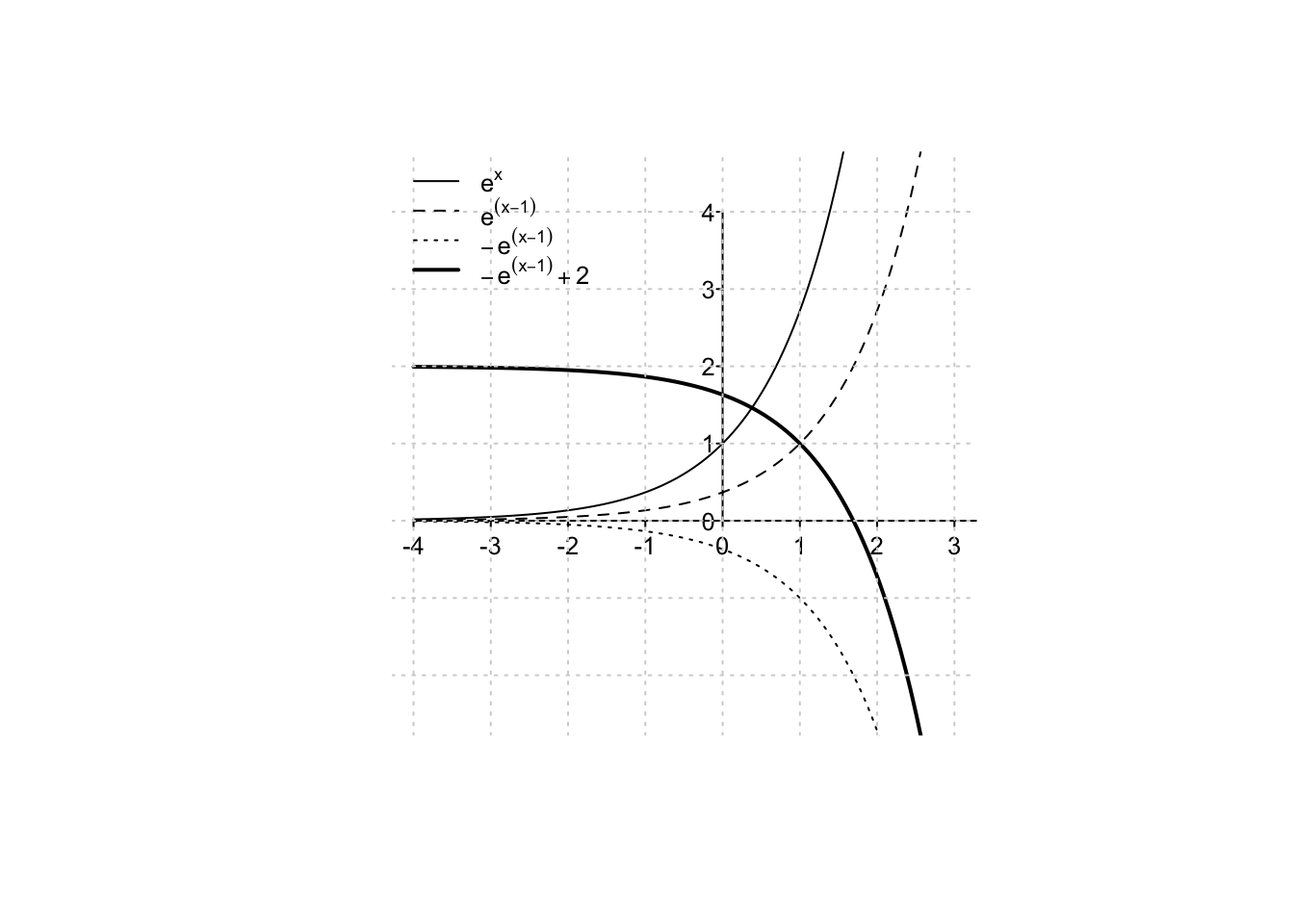
Example 2.14 Si disegni il grafico della funzione \(f:\mathbb{R} \to \mathbb{R}\), definita da
\[
f(x)= -e^{x-1}+2.
\]
2.11 Esercizi
Il primo punto di ogni compito scritto di Matematica richiederà il calcolo del dominio naturale della funzione oggetto di studio.
Si trovino i domini naturali \(D_f\) delle seguenti funzioni \(f: D_f \to \mathbb{R}\), definite da:
Exercise 2.1
\(f(x)=\sqrt{x^2-2x}-x\)Exercise 2.2
\(f(x)=\log \left( \frac{2-x}{x-4} \right)\)Exercise 2.3
\(f(x)=x e^{-1/x}\)Exercise 2.4
\(f(x)= \frac{x^2-4x+1}{x}\)Exercise 2.5
\(f(x)= \frac{-5x^2+x}{e^x}\)Exercise 2.6
\(f(x)=\frac{(x-3)}{(x-2)^2}\)Exercise 2.7
\(f(x)=\frac{x^2-x-1}{e^x}\)Exercise 2.8
\(f(x)=\frac{-2\log(x^3)}{x^2}\)Exercise 2.9
\(f(x)= \frac{e^{x-2}}{(x-1)^2}\)Exercise 2.10
\(f(x)=e^{\frac{x+1}{x}}\)Exercise 2.11
\(f(x)= \frac{1-e^x}{e^x-2}\)Exercise 2.12
\(f(x)= \frac{x+1}{1+x^2}\)Exercise 2.13
\(f(x)=\sqrt{x^2-9}-x\)Exercise 2.14
\(f(x)= \frac{e^{-x}}{x^2}\)Exercise 2.15
\(f(x)= \frac{\sqrt{x}}{1-x}\)Exercise 2.16
\(f(x)=\frac{3x^2}{2-x}\)Exercise 2.17
\(f(x)=\frac{e^{x-4}}{3-x}\)Exercise 2.18
\(f(x)=\frac{2x^2-x-2}{x-1}\)Exercise 2.19
\(f(x)=\frac{e^x}{x^2}\)Exercise 2.20
\(f(x)=\log \left( \frac{6-x}{x-3} \right)\)Exercise 2.21
\(f(x)=-3x + \sqrt{x^2-9}\)Exercise 2.22
\(f(x)=\frac{\log(x^2-4)}{4-x^2}\)Exercise 2.23
\(f(x)=\frac{x^3}{-x^2+x+2}\)