6 Integrali
Se nel Capitolo 4 ci siamo occupati del calcolo della derivata di una funzione \(f\), in questo dovremo trovare una funzione la cui derivata sia uguale a \(f\). Questo processo inverso prende il nome di integrazione. Calcolare l’integrale di una funzione è una operazione in generale complessa, in alcuni casi impossibile da effettuare analiticamente. Analogamente a quanto visto per i limiti, non esiste un metodo di risoluzione generale per calcolare un integrale, ma ci si dovrà ricondurre a varie casistiche di calcolo.
6.1 Definizione di integrale
Definition 6.1 Data una funzione \(f:A \subseteq \mathbb{R} \to \mathbb{R}\), si dice primitiva di \(f\) una qualsiasi funzione derivabile \(F:A \subseteq \mathbb{R} \to \mathbb{R}\), tale che \[ F'(x)=f(x), \quad x \in A. \]
Example 6.1 Data la funzione quadrato \(f:\mathbb{R}\to \mathbb{R}, f(x)=x^2\), è immediato verificare che la funzione \[ F(x)=\frac{x^3}{3} \] è una sua primitiva in quanto si ha \[ F'(x)=\left(\frac{x^3}{3}\right)'=\frac{3x^2}{3}=x^2=f(x). \] Si osservi che anche la funzione \[ G(x)=\frac{x^3}{3}+1 \] risulta essere una primitiva di \(f\) in quanto la derivata di una costante è nulla.
Dall’esempio precedente si deduce che una funzione ha infinite primitive (e si può dimostrare che tutte differiscono a meno di una costante).
Definition 6.2 Data una funzione \(f:A \subseteq \mathbb{R} \to \mathbb{R}\), si dice integrale (indefinito) di \(f\) l’insieme di tutte le sue primitive, e lo si indica col simbolo \[ \int f \quad \text{oppure } \int f(x) \,dx. \]
Dalle regole di derivazione delle funzioni elementari viste nel Capitolo 4 seguono le corrispondenti regole di integrazione.
Theorem 6.1 Si hanno le seguenti regole di integrazione: \[\begin{align*} \textbf{Integrale di una potenza:} \quad &\boldsymbol{\int x^q \,dx = \frac{x^{q+1}}{q+1}+C, \quad q \in \mathbb{Q}, \quad q \neq -1.}\\ \textbf{Integrale di } \boldsymbol{ x^{-1}}\textbf{:}\quad &\boldsymbol{ \int \frac{1}{x} \,dx = \log |x|+C.}\\ \textbf{Integrale dell'esponenziale:} \quad &\boldsymbol{\int e^x \,dx = e^x +C.}\\ \textbf{Integrale del logaritmo:} \quad &\boldsymbol{\int \log(x) \, dx = x(\log(x) -1) +C.} \end{align*}\]
Per dimostrare che una funzione è una primitiva di una funzione assegnata, basta calcolarne la derivata. Quindi se calcolare un integrale in generale può essere complesso, verificarlo risulta immediato.
Proof. Derivando le primitive date, si ha: \[ \left(\frac{x^{q+1}}{q+1}+C\right)'=\frac{(q+1)x^q}{q+1}=x^q,\; q \neq -1,\quad (\log |x| + C)'=\frac{1}{x}, \] dove per quest’ultimo passaggio si veda l’Esempio 4.14. Inoltre si calcola: \[ \left(e^x+C\right)'=e^x,\quad (x(\log(x) -1))'=\log(x), \] dove, per quest’ultimo passaggio, si veda l’Esempio 4.9, oppure l’Esempio 6.4 di seguito.
Oltre agli integrali delle funzioni elementari, ci sono alcuni integrali immediati che possono essere già calcolati e verificati, come ad esempio: \[\begin{align*} &\int e^{\lambda x}\, dx = \frac{e^{\lambda x}}{\lambda}+C, \quad \lambda \neq 0,\\ \\ &\int \frac{1}{mx+q} \, dx =\frac{\log|mx+q|}{m}+C,\quad m \neq 0. \end{align*}\] Inoltre, dalle corrispondenti regole di derivazione, discendono immediatamente le seguenti regole di integrazione.
Theorem 6.2 Se \(f,g: A \subseteq \mathbb{R} \to \mathbb{R}\) hanno integrali \(\int f(x)\, dx, \int g(x)\, dx\), allora \[ \textbf{Integrale di una somma:} \quad \boldsymbol{\int f(x)+g(x) \,dx = \int f(x) \,dx +\int g(x)\,dx.}\\ \] \[ \textbf{Integrale del prodotto per una costante:} \quad \boldsymbol{\int \lambda \,f(x) \,dx = \lambda \int f(x) \, dx, \quad \lambda \in \mathbb{R}.}\\ \]
Partendo da queste semplici regole di integrazione, possiamo passare ad analizzare le varie casistiche di integrali più complessi.
6.2 Integrazione per parti (A)
L’integrazione per parti si usa solitamente per provare a calcolare l’integrale del prodotto tra un polinomio ed una esponenziale, o del prodotto tra un polinomio ed un logaritmo. La regola di integrazione per parti deriva immediatamente dalla regola di derivazione del prodotto: \[ \left( f \cdot g \right)'(x) = f'(x)g(x) + f(x)g'(x), \] da cui si ricava, omettendo la costante \(C\), che \[ f(x)g(x)=\int f'(x)g(x) + f(x)g'(x) \, dx =\int f'(x)g(x)\, dx +\int f(x)g'(x) \, dx, \] da cui discende la regola di integrazione per parti: \[ \boldsymbol{\int f'(x)g(x)\, dx = f(x)g(x) - \int f(x)g'(x) \, dx}. \] Vediamo come applicare la regola in alcuni esempi.
Example 6.2 Si calcoli \[ \int e^{2x}\,x \, dx. \] Quando l’argomento dell’integrale è il prodotto tra un polinomio e una funzione esponenziale, conviene provare a risolverlo tramite integrazione per parti, scrivendo la funzione esponenziale come derivata del suo integrale: \[\begin{align*} \int f'(x)g(x)\, dx &= f(x)g(x) - \int f(x)g'(x) \, dx \\ \int e^{2x}x \, dx= \int \left(\frac{e^{2x}}{2}\right)'x \, dx&= \left(\frac{e^{2x}}{2}\right)x -\int \frac{e^{2x}}{2} (x)' \,dx \\\\ &= \left(\frac{e^{2x}}{2}\right)x -\int \frac{e^{2x}}{2} \, dx \\\\ &= \left(\frac{e^{2x}}{2}\right)x -\frac{e^{2x}}{4}=\left(\frac{e^{2x}}{4}\right)(2x-1) +C. \end{align*}\] Si può verificare la correttezza di quanto svolto calcolando la derivata di una primitiva trovata: \[\begin{align*} \left(\left(\frac{e^{2x}}{4}\right)(2x-1)\right)'&= \left(\frac{e^{2x}}{4}\right)'(2x-1)+\left(\frac{e^{2x}}{4}\right)(2x+1)' \\\\&=\frac{2e^{2x}}{4}(2x-1)+\left(\frac{e^{2x}}{4}\right)(2)=\frac{e^{2x}}{4}(4x-2+2)=\frac{e^{2x}}{4}(4x)=e^{2x}x, \end{align*}\] e verificando che essa è uguale all’argomento dell’integrale di partenza.
Remark. Osserviamo i seguenti punti rilevanti sull’esempio appena svolto:
la regola di integrazione per parti può essere equivalentemente scritta come: \[ \boldsymbol{\int f(x)g'(x)\, dx = f(x)g(x) - \int f'(x)g(x) \, dx}; \]
coerentemente con il fatto che la derivata del prodotto di un polinomio per una esponenziale è sempre un polinomio (differente) per la stessa esponenziale (si veda l’Esempio 4.17), l’integrale del prodotto di un polinomio per una esponenziale è sempre un polinomio (differente) per la stessa esponenziale (che può essere messa in evidenza);
nel caso dell’integrale del prodotto di un polinomio per una esponenziale, l’integrazione per parti consente di calcolare l’integrale come prodotto tra due funzioni (che possono essere qualsiasi non essendo l’argomento di un integrale) e l’integrale della stessa esponenziale moltiplicata per la derivata del polinomio. Dato che la derivata di un polinomio è un polinomio di grado inferiore, applicando il procedimento tante volte quanto è il grado del polinomio, si arriverà alla risoluzione di un integrale immediato;
per snellire la notazione, nel seguito aggiungeremo la costante \(C\) solo al termine del procedimento di integrazione;
non è detto che l’integrazione per parti abbia sempre successo: alcuni integrali (anche all’apparenza semplici) non sono esprimibili in forma analitica chiusa ovvero come somma, prodotto, quoziente o composizione di funzioni elementari, come ad esempio: \[ \int e^{-x^2} \, dx; \]
nel calcolo di qualsiasi integrale, si può sempre effettuare una verifica controllando che la derivata di una primitiva trovata sia uguale all’argomento dell’integrale di partenza, ottenendo così la certezza di aver risolto correttamente l’esercizio;
le funzioni da integrare si intendono sempre definite sul loro dominio naturale, così come le loro primitive.
Example 6.3 Si calcoli \[ \int (3x^2-4x+1) e^x\, dx. \] Quando l’argomento dell’integrale è il prodotto tra un polinomio e una funzione esponenziale, conviene provare a risolverlo tramite integrazione per parti. In questo caso, essendo il polinomio di grado 2, per risolvere l’integrale sarà necessario applicare la regola di integrazione per parti 2 volte: \[\begin{equation} \int (3x^2-4x+1) \,e^x\, dx = \int (3x^2-4x+1)\, (e^x)'\, dx = (3x^2-4x+1) \,e^x - \int (6x-4) \,e^x \, dx. \tag{6.1} \end{equation}\] Come prevedibile, l’integrale di partenza è stato ridotto ad uno analogo in cui il grado del polinomio è diminuito. Si procede quindi applicando lo stesso procedimento al nuovo integrale trovato e risolvendo infine un integrale immediato: \[\begin{align*} \int (6x-4)\, e^x \, dx&=\int (6x-4)\, (e^x)' \, dx \\&= (6x-4)\,e^x - \int (6x-4)'e^x \,dx\\&=(6x-4)\,e^x-\int 6\,e^x \, dx =(6x-4)\,e^x- 6\,e^x =(6x-10)\,e^x. \end{align*}\] Sostituendo in (6.1), e mettendo in evidenza l’esponenziale, si ottiene: \[\begin{align*} \int (3x^2-4x+1) \,e^x\, dx &=(3x^2-4x+1) \,e^x - \int (6x-4) \,e^x \, dx \\&=(3x^2-4x+1) \,e^x-(6x-10)e^x=(3x^2-10x+11)\,e^x+C. \end{align*}\] Si può verificare che \[ \left((3x^2-10x+11)\,e^x\right)'=(3x^2-4x+1) \,e^x. \]
Per parti si può trattare anche il prodotto di un polinomio per un logaritmo, ma esprimendo stavolta il polinomio come derivata del suo integrale.
Example 6.4 Si calcoli \[ \int \log(x) \, dx. \] In questi casi si applica la regola di integrazione per parti facendo scomparire (derivandolo) il logaritmo: \[\begin{align*} \int \log(x) \, dx&= \int (x)'\,\log(x) \, dx \\&=x \, \log(x) - \int x \,(\log(x))'\, dx \\&=x \, \log(x) -\int x \, \frac{1}{x} \, dx =x \, \log(x) -\int 1 \, dx \\&=x \, \log(x) -x = x \,(\log(x) -1)+C; \end{align*}\] si veda per verifica l’Esempio 4.9.
Example 6.5 Si calcoli \[ \int \sqrt[3]{x} \,\log(x) \, dx. \] Analogamente all’esempio precedente, si scrive \[ \int \sqrt[3]{x} \,\log(x) \, dx= \int x^{\frac13} \,\log(x) \, dx= \int \left(\int x^{\frac13}\right)' \,\log(x) \, dx = \int \left(\frac34x^{\frac43}\right)' \log(x) \, dx, \] da cui si ottiene \[\begin{align*} \int \sqrt[3]{x} \,\log(x) \, dx&=\int \left(\frac34x^{\frac43}\right)' \log(x) \, dx \\&=\frac34x^{\frac43}\, \log(x) - \int \left(\frac34x^{\frac43}\right)\frac1x \, dx \\&= \frac34x^{\frac43}\, \log(x) - \int \frac34x^{\frac13} \, dx \\&= \frac34x^{\frac43}\, \log(x) -\frac{9}{16} x^{\frac43}= \frac34x^{\frac43}\left(\log(x) -\frac34 \right)+C. \end{align*}\] Si raccomanda di effettuare sempre la verifica del risultato raggiunto.
6.3 Integrazione per sostituzione (B)
L’integrazione per sostituzione si usa solitamente quando nell’argomento dell’integrale compare (a meno di una costante moltiplicativa) la derivata di una funzione interna. La regola di integrazione per sostituzione deriva infatti dalla regola di derivazione della composizione di funzioni. Vediamo come applicarla in alcuni esempi.
Example 6.6 Si calcoli \[ \int \frac{2x^2}{1+x^3} \, dx. \] Questo è un integrale classico che, dopo alcuni esercizi, diverrà immediato da calcolare. Si nota infatti al numeratore la derivata del denominatore (a meno di una costante moltiplicativa). In questi casi conviene rinominare la funzione interna di cui appare la derivata, ovvero effettuare la sostituzione: \[ \begin{cases} y=1+x^3, \\ dy=(1+x^3)'\,dx=3x^2\,dx \Rightarrow dx=\frac{dy}{3x^2}, \end{cases} \] così ottenendo \[ \int \frac{2x^2}{1+x^3} \, dx =\int \frac{2x^2}{y} \, \frac{dy}{3x^2}=\int \frac{2}{3y} \, dy= \frac23\int\frac1y \, dy=\frac23\log|y|=\frac23\log|1+x^3|+C. \] La sostituzione è solo un modo meccanico per rendere esplicita nell’argomento dell’integrale la derivata di una composizione. Si poteva direttamente scrivere \[ \int \frac{2x^2}{1+x^3} \, dx =\frac23\int \frac{3x^2}{1+x^3} \, dx= \frac23 \log |1+x^3|+C. \] Analogamente agli esempi studiati in precedenza, il risultato si può verificare derivando l’integrale ottenuto: \[ \left(\frac23 \log |1+x^3|+C\right)'=\frac23 \frac{3x^2}{1+x^3}=\frac{2x^2}{1+x^3}. \]
Example 6.7 Si calcoli \[ \int \frac{x}{(x^2-2)^3}\, dx. \] Anche questo è un integrale che, con la pratica, potrà essere risolto immediatamente. Si osserva, come nell’esempio precedente, che al numeratore compare la derivata della base della potenza. Si effettua quindi la sostituzione \[ \begin{cases} y=x^2-2, \\ dy=(2x)\,dx \Rightarrow dx=\frac{dy}{2x}, \end{cases} \] ottenendo \[\begin{align*} \int \frac{x}{(x^2-2)^3}\, dx&=\int \frac{x}{y^3}\,\frac{dy}{2x} \\\\&= \int \frac{1}{2y^3}\,dy =\frac12\int y^{-3} \, dy= \frac12 \frac{y^{-2}}{-2}=-\frac14y^{-2}=-\frac{1}{4(x^2-2)^2}+C. \end{align*}\] Anche in questo caso, sarebbe stato sufficiente scrivere \[ \int \frac{x}{(x^2-2)^3}\, dx=\frac12 \int (2x)(x^2-2)^{-3} \, dx=\frac12 \frac{(x^2-2)^{-2}}{-2}=-\frac14\frac{1}{(x^2-2)^2}+C. \] La verifica è lasciata come esercizio.
Remark. Osserviamo i seguenti punti rilevanti sull’esempio appena svolto:
Nel calcolare un integrale per sostituzione, non ci si deve dimenticare di ritornare, alla fine dei calcoli, alla variabile di integrazione originaria;
basta davvero poco per rendere complesso il calcolo di un integrale. Aggiungendo un grado al numeratore nell’integrale precedente si ottiene \[ \int \frac{x^2}{(x^2-2)^3}\, dx = \frac{1}{64}\left(- \frac{4x(2+x^2)}{(x^2-2)^2}- \sqrt{2}\log(\sqrt2-x)+\sqrt2\log(\sqrt2+x)\right) + C. \]
Example 6.8 Si calcoli
\[
\int \sqrt{5x+4}\, dx.
\]
Anche in questo caso, a meno di una costante moltiplicativa, compare la derivata
del polinomio di primo grado sotto radice. Si effettua quindi la sostituzione
\[
\begin{cases}
y=5x+4, \\
dy=5\,dx \Rightarrow dx=\frac{dy}{5},
\end{cases}
\]
ottenendo
\[
\int \sqrt{5x+4}\, dx =\frac15\int y^{\frac12} \, dy= \frac15 \,\frac23 \,y^{\frac32}= \frac{2}{15} \sqrt{y^3}=\frac{2}{15} \sqrt{(5x+4)^3}+C.
\]
La verifica è lasciata come esercizio.
Il metodo per sostituzione può essere utile anche nei casi in cui nell’argomento dell’integrale si ripeta una stessa funzione più volte. Il prossimo esempio illustra la sostituzione standard della funzione esponenziale.
Example 6.9 Si calcoli \[ \int \frac{e^{2x}+e^x}{e^{2x}-1}\, dx. \] Effettuando la sostituzione \[ \begin{cases} y=e^x, \\ dy=e^x\,dx \Rightarrow dx=\frac{dy}{e^x}=\frac{dy}{y}, \end{cases} \] si ottiene \[\begin{align*} \int \frac{e^{2x}+e^x}{e^{2x}-1}\, dx &= \int \frac{y^2+y}{y^2-1}\,\frac1y \,dy =\int \frac{y+1}{y^2-1} \,dy \\&=\int \frac{y+1}{(y+1)(y-1)} \,dy =\int \frac{1}{y-1}\, dy =\log|y-1|=\log |e^x-1|+C. \end{align*}\] Preferendo una soluzione più veloce come integrale immediato si poteva subito scrivere \[ \int \frac{e^{2x}+e^x}{e^{2x}-1}\, dx =\int \frac{e^{x}(e^x+1)}{(e^{x}+1)(e^x-1)}\, dx=\int \frac{e^{x}}{(e^x-1)}\, dx =\log|e^x-1|+C, \] dove l’ultima uguaglianza discende dall’osservare che al numeratore dell’argomento dell’integrale compare la derivata del denominatore. La verifica è in questo caso immediata.
La sostituzione \(y=e^x\) nella pratica divide l’argomento dell’integrale per \(y\).
6.4 Integrale del quoziente di polinomi (C)
Nei seguenti esempi illustriamo alcuni procedimenti di risoluzione nel caso in cui la funzione da integrare sia un rapporto tra due polinomi.
Example 6.10 Si calcoli \[ \int \frac{x+3}{x^2+x-2}\, dx. \] In questa tipologia di integrali, è necessario “spezzare” la frazione in più parti in modo che ognuna di esse diventi un integrale immediato da calcolare. In questo esempio, si scompone prima di tutto il denominatore come \[ \int \frac{x+3}{x^2+x-2}\, dx =\int \frac{x+3}{(x+2)(x-1)}\, dx. \] Quindi si cerca di scrivere il numeratore della frazione in modo da far apparire i fattori del denominatore: \[\begin{equation} \frac{x+3}{(x+2)(x-1)}=\frac{A}{(x+2)}+\frac{B}{(x-1)}=\frac{A(x-1)+B(x+2)}{(x+2)(x-1)}. \tag{6.2} \end{equation}\] L’eguaglianza precedente è vera se \[ A(x-1)+B(x+2)=(A+B)x-A+2B=x+3, \] ovvero se ha soluzione il seguente sistema lineare (si veda il Capitolo 7): \[ \begin{cases} \phantom{-}A+B=1,\\ -A+2B=3. \end{cases} \] Sostituendo \(B=1-A\) nella seconda equazione, si trova \(-A+2-2A=3\), ovvero \(-3A=1\), e quindi \(A=-\frac13\) e \(B=\frac43\). Ricordando la (6.2) si ottiene cioè \[\begin{align*} \int \frac{x+3}{x^2+x-2}\, dx &=\int \frac{x+3}{(x+2)(x-1)}\, dx \\ \\&= \frac13 \int \left(-\frac{1}{x+2} +\frac{4}{x-1}\right) \, dx \\ \\&=\frac13 \left( \int \frac{-1}{x+2}\, dx + \int \frac{4}{x-1} \, dx \right)= - \frac13 \log|x+2| +\frac43 \log |x-1|+C. \end{align*}\] La verifica è lasciata come esercizio.
Il procedimento illustrato nel precedente esempio è laborioso. Quando è possibile, conviene cercare di diminuire i calcoli e, di conseguenza, le probabilità di errore.
Example 6.11 Si calcoli \[ \int \frac{x+1}{x^2-2x+1} \, dx. \] Si riconosce subito la presenza di un quadrato al denominatore: \[ \int \frac{x+1}{x^2-2x+1} \, dx=\int \frac{x+1}{(x-1)^2} \, dx. \] In questo caso, si potrebbe attuare un procedimento analogo a quello dell’esempio precedente. È però molto più conveniente osservare che \[\begin{align*} \int \frac{x+1}{x^2-2x+1} \, dx&=\int \frac{x+1}{(x-1)^2} \, dx = \int \frac{(x-1)+2}{(x-1)^2} \, dx \\ \\&= \int \frac{(x-1)}{(x-1)^2} \, dx + \int \frac{2}{(x-1)^2} \, dx= \int \frac{1}{(x-1)} \, dx + \int \frac{2}{(x-1)^2} \, dx \\ \\&= \int \frac{1}{(x-1)} \, dx + 2\int (x-1)^{-2} \, dx =\log |x-1| -2 (x-1)^{-1}+C. \end{align*}\] La verifica è lasciata come esercizio.
Remark. Osserviamo i seguenti punti rilevanti sull’integrazione di rapporti tra polinomi:
una casistica completa è molto più ampia di quella descritta in questo capitolo, ma va oltre gli scopi di questo testo. Per tutte le tipologie di integrali di rapporti tra polinomi, si può far riferimento ad un testo di Matematica delle superiori;
osserviamo ancora che piccole variazioni nella funzione da integrare producono grandi differenze di risultato. L’integrale \[ \int \frac{x-1}{x^2-2x+1} \, dx= \int \frac{x-1}{(x-1)^2} \, dx =\int \frac{1}{x-1} \, dx = \log |x-1| +C \] è immediato, mentre l’integrale \[ \int \frac{x+1}{x^2+1} \, dx= \frac12 \log (x^2+1) +\arctan(x)+C \]
è esprimibile come funzione reale solo tramite funzioni trigonometriche, quindi esula anch’esso dagli scopi di questo testo.
Nei seguenti esempi, studiamo qualche caso leggermente più complesso.
Example 6.12 Si calcoli \[ \int \frac{1}{x^2-16} \, dx. \] Prima di tutto, si scompone il denominatore della frazione, ottenendo \[ \int \frac{1}{x^2-16} \, dx= \int \frac{1}{(x+4)(x-4)} \, dx. \] Al numeratore della frazione vorremmo far comparire i fattori del denominatore, ovvero scrivere \[ \frac{\boldsymbol{(x+4)\square(x-4)}}{(x+4)(x-4)}. \] Dato che la variabile \(x\) deve scomparire dal numeratore, è utile usare la differenza \(\square=-\), ottenendo \[ \frac{\boldsymbol{(x+4)-(x-4)}}{(x+4)(x-4)}=\frac{8}{(x+4)(x-4)}. \] A questo punto, basta dividere per la costante al numeratore. In conclusione si ottiene: \[\begin{align*} \int \frac{1}{x^2-16} \, dx&= \int \frac{1}{(x+4)(x-4)} \, dx\\ \\&=\frac18\int \frac{(x+4)-(x-4)}{(x+4)(x-4)} \, dx \\ \\&= \frac18\left( \int \frac{1}{x-4}\,dx-\int \frac{1}{x+4}\,dx\right)\\ \\&=\frac18 \left(\log|x-4| -\log |x+4|\right)= \frac18 \log\left|\frac{x-4}{x+4}\right|+C. \end{align*}\]
Si osservi come nell’esempio precedente, e in generale in tutti quelli trattati in questo capitolo, il dominio naturale delle primitive trovate sia lo stesso della funzione da integrare, coerentemente con la definizione di integrale indefinito.
Al fine di evitare un errore molto grave, si osservi anche che \[ \int \frac{1}{(x+4)(x-4)} \, dx \neq \left(\int \frac{1}{x+4}\,dx \right) \cdot \left(\int \frac{1}{x-4}\,dx \right). \]
Example 6.13 Si calcoli \[ \int \frac{e^{2x}}{3-e^x} \, dx. \] È immediato visualizzare la necessità di ricorrere alla sostituzione standard \[ \begin{cases} y=e^x, \\ dy=e^x\,dx \Rightarrow dx=\frac{dy}{e^x}=\frac{dy}{y}, \end{cases} \] così ottenendo \[ \int \frac{e^{2x}}{3-e^x} \, dx= \int \frac{y^2}{(3-y)y} \, dy= \int \frac{y}{(3-y)} \, dy. \] Ci si è ricondotti dunque ad un integrale di quoziente di polinomi. Anche in questo caso, sarebbe utile che al numeratore della frazione da integrare comparisse il termine al denominatore. È possibile procedere come \[\begin{align*} \int \frac{e^{2x}}{3-e^x} \, dx=\int \frac{y}{(3-y)} \, dy &=-\int \frac{(3-y)-3}{(3-y)} \, dy \\\\&= - \left(\int 1 \, dy-\int \frac{3}{3-y}\, dy \right) \\\\&= - (y-(-3 \log|3-y|))= \\\\&= - (y+3 \log|3-y|)= -e^x-3\log|3-e^x|+C. \end{align*}\] La verifica è lasciata come esercizio.
Nel precedente integrale, si osservi che si è usato il fatto che \[ \int \frac{3}{3-y}\, dy = -3\log|3-y|. \] Per capire pienamente il motivo della comparsa del segno “\(-\)” basta derivare la funzione \(f(x)=3\log|3-y|\), ottenendo \[ (3\log|3-y|)'=\frac{3}{3-y}(3-y)'=-\frac{3}{3-y}. \] Per ottenere il segno corretto nell’argomento dell’integrale è necessario quindi cambiare il segno della primitiva. Questo cambiamento di segno nel calcolare primitive o derivate è necessario ogni volta in cui nell’argomento di una funzione compare la variabile cambiata di segno, come ad esempio in \(|3-y|\).
Example 6.14 Si calcoli \[ \int \frac{5-e^x}{2+e^x} \, dx. \] Anche in questo caso, ricorrendo alla sostituzione standard \[ \begin{cases} y=e^x, \\ dy=e^x\,dx \Rightarrow dx=\frac{dy}{e^x}=\frac{dy}{y}, \end{cases} \] si ottiene \[ \int \frac{5-e^x}{2+e^x} \, dx=\int \frac{5-y}{(2+y)\,y} \, dy. \] Analogamente a quanto fatto in precedenza, si deve cercare di ottenere al numeratore una somma o differenza dei fattori presenti al denominatore, ovvero scrivere \[ \frac{\boldsymbol{(2+y)\square(y)}}{(2+y)\,y}. \] In questo caso, per ottenere la costante \(5\) al numeratore, è necessario moltiplicare il fattore \((2+y)\) per \(\frac52\), ottenendo al numeratore \[ \frac52(2+y)\square(y) =\left(5+\frac52y\right)\square(y). \] Per ottenere anche \(-y\), bisognerà infine moltiplicare il secondo fattore \(y\) per \(-\frac72\). In conclusione, si ha \[ \frac{\boldsymbol{\frac52(2+y)-\frac72(y)}}{(2+y)\,y}=\frac{\boldsymbol{5-y}}{(2+y)\,y}, \] da cui \[\begin{align*} \int \frac{5-e^x}{2+e^x} \, dx&=\int \frac{5-y}{(2+y)\,y} \, dy \\\\&= \int \frac52 \frac{(2+y)\,\,\,\,}{(2+y)\,y} \, dy -\int \frac72 \frac{y}{(2+y)\,y} \, dy \\\\&= \frac52 \int \frac{1}{y}\, dy-\frac72\int \frac{1}{2+y} \, dy= \frac52 \log |y|-\frac72\log |2+y| \\\\&=\frac52 \log |e^x| -\frac72 \log |2+e^x|=\frac52 x -\frac72 \log(2+e^x) +C, \end{align*}\] con verifica lasciata per esercizio.
6.5 Altre tipologie di integrali (D)
Non è detto che un integrale possa essere risolto analiticamente, oppure possa essere risolto con le strategie di risoluzione illustrate nelle casistiche precedenti, o comunque che possa essere risolto solo con una di esse. Alcuni integrali ad esempio possono essere calcolati sia operando per parti che per sostituzione.
Example 6.15 Si calcoli \[ \int -x^4\log(x^5)\, dx. \] Si osservi che compare (a meno di una costante moltiplicativa) la derivata dell’argomento del logaritmo, quindi si può operare la sostituzione \[ \begin{cases} y=x^5, \\ dy=5x^4\,dx \Rightarrow dx=\frac{dy}{5x^4}, \end{cases} \] ottenendo \[ \int -x^4\log(x^5)\, dx= \int -x^4\log(y)\, \frac{dy}{5x^4}= -\frac15 \int\log(y)\,dy. \] Ricordando l’integrale di \(\log(x)\), si calcola \[\begin{align*} \int -x^4\log(x^5)\, dx&= -\frac15 \int\log(y)\,dy \\&=-\frac15\, y\,(\log y -1)=-\frac15\, x^5\,(\log(x)^5 -1)=-\frac15\, x^5\,(5\log(x) -1)+C. \end{align*}\] L’argomento dell’integrale è il prodotto tra un polinomio e un logaritmo, quindi si poteva anche procedere equivalentemente per parti: \[\begin{align*} \int -x^4\log(x^5)\, dx&= -5 \int x^4\log(x)\, dx \\\\&= -5 \int \left(\frac{x^5}{5}\right)'\log(x)\, dx \\\\&=-5 \left(\frac{x^5}{5}\,\log(x) -\left(\int \frac{x^5}{5} \frac{1}{x}\, dx\right)\right)=-x^5\,\log(x) +\int x^4\, dx \\\\& = -x^5\,\log(x) +\frac{x^5}{5}=-\frac15\, x^5\,(5\log(x) -1)+C. \end{align*}\] Si può scegliere il metodo di risoluzione preferito ed effettuare la verifica del risultato.
Un’altra tipologia di integrale che si può risolvere sia per parti che per sostituzione è la seguente.
Example 6.16 Si calcoli \[ \int x \,\sqrt[3]{4x-2}\, dx. \] In questi casi, conviene sostituire l’intera radice con una nuova variabile \[ y=\sqrt[3]{4x-2}. \] Per calcolare la sostituzione è conveniente scrivere la sostituzione come \[y^3=4x-2,\] ovvero \[ \begin{cases} y=\sqrt[3]{4x-2}, \\\\ y^3=4x-2 \Rightarrow \boldsymbol{x=\frac{y^3+2}{4}},\\\\ 3y^2dy=4\,dx \Rightarrow \boldsymbol{dx=\frac{3y^2 \,dy}{4}}. \end{cases} \] A fronte di una sostituzione più complessa, si ottiene un integrale immediato: \[\begin{align*} \int \boldsymbol{x} \,\sqrt[3]{4x-2}\, \boldsymbol{dx} &= \int \boldsymbol{\frac{y^3+2}{4}} \,y\, \boldsymbol{\frac{3y^2}{4} \,dy} \\\\&= \frac{3}{16}\int (y^3+2)y^3 \, dy = \frac{3}{16} \int y^6+2y^3 \, dy = \frac{3}{16} \left( \frac{y^7}{7} + \frac12 y^4 \right) \\\\&=\frac{3}{16} \left( \frac{2y^7+7y^4}{14} \right)=\frac{3}{224}\,y^4\, (2y^3+7) \\\\&= \frac{3}{224}\,(4x-2)^{\frac43}\, (2(4x-2)+7)= \frac{3}{224}\,(4x-2)^{\frac43}\, (8x+3)+C. \end{align*}\]
Lo stesso risultato è calcolabile operando per parti, ovvero scrivendo \[\begin{align*} \int x \,\sqrt[3]{4x-2}\, dx&=\int x \,\left(\int (4x-2)^{\frac13} \, dx \right)'\, dx \\\\&=\int x \left(\frac{(4x-2)^{\frac43}}{4 \cdot\frac43}\right)'\, dx \\\\&=\frac{3}{16}\int x\,\left((4x-2)^{\frac43}\right)' \, dx = \frac{3}{16}\left(x\,(4x-2)^{\frac43}-\int (4x-2)^{\frac43}\, dx\right) \\\\&=\frac{3}{16}\left(x\,(4x-2)^{\frac43}-\frac{3}{28}(4x-2)^{\frac73}\right)=\frac{3}{16}(4x-2)^{\frac43}\left(x-\frac{3}{28}(4x-2)\right) \\\\&=\frac{3}{16}(4x-2)^{\frac43}\left(x-\frac37 x+\frac{3}{14} \right) \\\\&=\frac{3}{16}(4x-2)^{\frac43}\left(\frac47 x+\frac{3}{14} \right)=\frac{3}{224}(4x-2)^{\frac43}\left(8x+3 \right)+C. \end{align*}\]
Si può scegliere il metodo di risoluzione preferito ed effettuare la verifica del risultato.
Si osservi il diverso trattamento dei seguenti integrali con radice:
si ha un integrale immediato quando compare (a meno di una costante moltiplicativa) la derivata dell’argomento della radice: \[ \int x\sqrt[3]{\boldsymbol{4x^2-2}}\, dx= \frac{3}{32} (4x^2-2)^{\frac43}+C\,; \]
negli altri casi, si può operare una sostituzione o procedere per parti: \[ \int x \,\sqrt[3]{\boldsymbol{4x-2}}\, dx= \frac{3}{224}\,(4x-2)^{\frac43}\, (8x+3)+C\,; \]
ma non sempre si può arrivare ad una primitiva esprimibile in forma analitica chiusa, come in \[ \int x \,\sqrt[3]{\boldsymbol{4x^3-2}}\, dx. \]
6.6 Integrali definiti
Come discusso nella Prefazione, in questo testo prenderemo come assunto il Teorema Fondamentale del Calcolo Integrale, senza darne la relativa costruzione e dimostrazione.
Definition 6.3 Sia \(f:[a,b]\to \mathbb{R}\) una funzione continua avente primitiva \(F\) (\(F'(x)=f(x), x \in [a,b]\)). Si dice integrale definito di \(f\) sull’intervallo \([a,b]\) il valore reale \[ \int_{a}^{b} f(x) \, dx= F(x) \Big|_a^b=F(b)-F(a). \]
Si può costruire \(\int_{a}^{b} f(x) \, dx\) come l’area algebrica della regione di piano delimitata dall’asse delle ascisse e il grafico di \(f\), compresa tra i punti \(x=a\) ed \(x=b\).
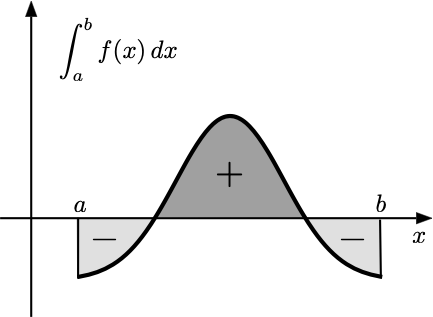
Example 6.17 L’area della regione di piano delimitata
dall’asse delle ascisse e il grafico della parabola \(f(x)=x^2\), compresa tra i punti \(x=0\) ed \(x=1\)
è pari a
\[
\int_0^1 x^2 \, dx= \frac{x^3}{3} \,\Big|_0^1 = \frac{1^3}{3}-\frac{0^3}{3}=\frac13.
\]
L’area della regione di piano delimitata
dall’asse delle ascisse e il grafico della funzione cubo \(f(x)=x^3\), compresa tra i punti \(x=-1\) ed \(x=1\)
è pari a
\[
\int_{-1}^1 x^3 \, dx= \frac{x^4}{4} \,\Big|_{-1}^1 = \frac{1^4}{4}-\frac{(-1)^4}{4}=0.
\]
Infatti, la funzione \(x^3\) è dispari e le aree di segno opposto prese a sinistra e a destra dello zero si annullano.
Calcolare un integrale definito non implica nessuna difficoltà aggiuntiva rispetto al calcolo di un integrale indefinito: entrambi si basano sulla ricerca di una primitiva della funzione argomento dell’integrale. L’integrale definito è utilizzato frequentemente nel Calcolo delle Probabilità e in Statistica per calcolare la probabilità di eventi riguardanti variabili aleatorie continue.
Example 6.18 Una variabile aleatoria \(X\) assolutamente continua ha distribuzione esponenziale \(\text{Exp}(\lambda)\), per \(\lambda>0\), se la sua funzione di densità è data da \[ f(x)=\lambda \,e^{-\lambda x}, \quad x \geq 0. \] La probabilità che \(X\) assuma valori nell’intervallo \([a,b]\), \(0 \leq a \leq b < +\infty\), è data da \[ P\left(X \in [a,b]\right) =\int_a^b \lambda\, e^{-\lambda x}\, dx =-e^{-\lambda x} \Big|_{a}^{b}=\left(e^{-\lambda a}-e^{-\lambda b}\right). \] Se \(X\) ha invece distribuzione normale standard \(N(0,1)\), ovvero possiede densità \[ f(x)=\frac{1}{\sqrt{2 \pi}}\,e^{-\frac12 x^2}, \quad x \in \mathbb{R}, \] allora la stessa probabilità \[ \int_a^b \frac{1}{\sqrt{2 \pi}}\,e^{-\frac12 x^2} \, dx \] non è esprimibile in forma chiusa, ma può essere calcolata numericamente. In R si calcola che \(P(X \in [-3,3])\simeq 99.73\%\).
## [1] 0.9973002La definizione di integrale definito può essere estesa ad una funzione integranda continua su un intervallo illimitato. Di questo caso tratteremo un esempio particolare che riveste una particolare importanza in varie discipline.
Example 6.19 Si definisca e si calcoli, al variare di \(k >0\), l’integrale definito
\[
\int_1^{+\infty} \frac{1}{x^k} \,dx.
\]
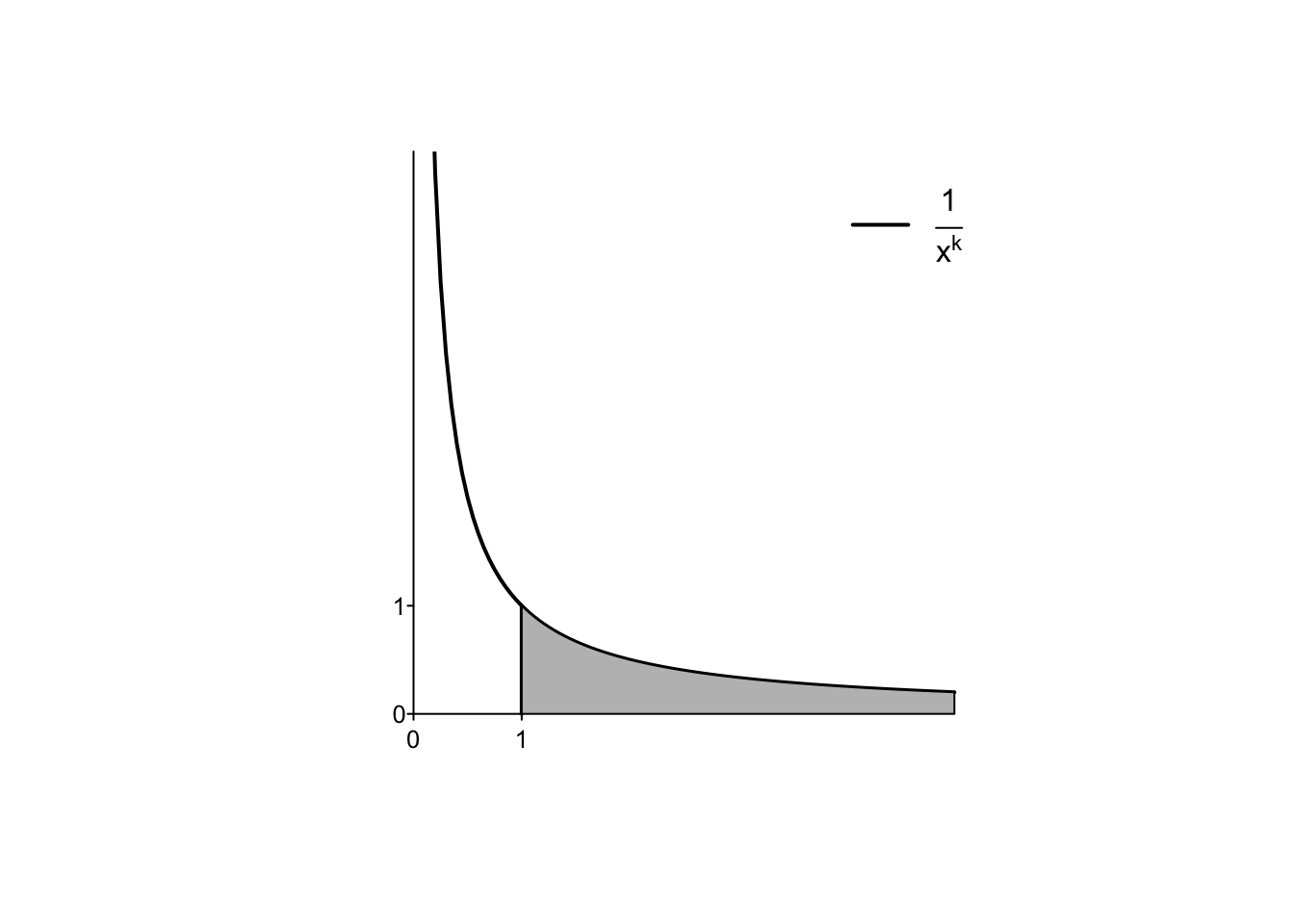Dato che si è definito l’integrale su un intervallo del tipo \([1,b]\), è naturale porre la seguente definizione:
\[\begin{equation}
\int_1^{+\infty} \frac{1}{x^k} \,dx = \lim_{b \to +\infty}\,\int_1^{b} \frac{1}{x^k} \,dx,
\tag{6.3}
\end{equation}\]
nel caso in cui questo limite esista, finito o infinito. Se interpretato come l’area nella figura precedente, l’integrale potrebbe risultare infatti infinito.
Si calcola allora che
\[
\int_1^{b} \frac{1}{x^k} \,dx =\int_1^{b} x^{-k} \,dx =
\begin{cases}
\frac{x^{-k+1}}{-k+1}\Big|_1^b=\frac{1}{1-k}\left( b^{1-k}-1 \right), &\text{ se } k \neq 1; \\\\
\log(x)\Big|_1^b=\log b, &\text{ se } k=1.
\end{cases}
\]
Passando al limite per \(b \to +\infty\) si ottiene
\[
\int_1^{b} \frac{1}{x^k} \,dx =
\begin{cases}
\lim_{b \to +\infty}\,\frac{1}{1-k}\left( b^{1-k}-1 \right)=\frac{1}{k-1}, &\text{ se } \,k > 1; \\
\\
\lim_{b \to +\infty}\log b=+\infty, &\text{ se } \,k=1;\\
\\
\lim_{b \to +\infty}\,\frac{1}{1-k}\left( b^{1-k}-1 \right)=+\infty, &\text{ se } \,0<k<1. \\
\end{cases}
\]
Il fatto che un integrale su un intervallo illimitato \([a, +\infty)\) sia finito
o infinito dipende quindi dalla velocità con cui la funzione integranda tende ad annullarsi per \(x \to +\infty\). Una funzione integranda che si annulla più velocemente di \(\frac{1}{x}\) (come ad esempio \(f(x)=\frac{1}{x^2}\), \(k=2\)) ha un integrale finito, altrimenti (\(f(x)=\frac{1}{\sqrt{x}}\), \(k=\frac12\)) infinito.
Nel Calcolo delle Probabilità e in Statistica, gli integrali definiti con supporto illimitato sono usati ad esempio nel calcolo del valore atteso di una variabile aleatoria con supporto illimitato.
Example 6.20 Continuando l’Esempio 6.18, si calcoli il valore atteso di una
variabile aleatoria \(X\) avente distribuzione esponenziale, ovvero si calcoli
\[
\mathbb{E}(X)=\int_0^{+\infty} x\,f(x) \, dx=\int_0^{+\infty} x\,\left(\lambda \,e^{-\lambda x}\right)\, dx=\lambda\left(\int_0^{+\infty} x\,\,e^{-\lambda x}\, dx\right).
\]
Innanzitutto si osserva che
\[
\lambda\left(\int x\,\,e^{-\lambda x}\, dx\right)= \lambda\left(\int x\,\,\left(\frac{e^{-\lambda x}}{-\lambda}\right)'\, dx\right)=-\left(\int x\,\left(e^{-\lambda x}\right)'\, dx\right).
\]
Procedendo per parti, si ottiene quindi
\[
-\left(\int x\,\left(e^{-\lambda x}\right)'\, dx\right)=-\left(x\,e^{-\lambda x}-\int e^{-\lambda x}\, dx\right)=-x\,e^{-\lambda x}+\left(\frac{e^{-\lambda x}}{-\lambda}\right)=-x\,e^{-\lambda x}-\frac{e^{-\lambda x}}{\lambda}.
\]
Utilizzando questa ultima primitiva, si ha dunque che
\[\begin{align*}
\mathbb{E}(X)=\int_0^{+\infty} x\,\left(\lambda \,e^{-\lambda x}\right)\, dx&= \lim_{b \to +\infty} \int_0^{b} x\,\left(\lambda \,e^{-\lambda x}\right)\, dx\\&=\lim_{b \to +\infty} \left(-x\,e^{-\lambda x}-\frac{e^{-\lambda x}}{\lambda}\right)\Big|_0^b=\lim_{b \to +\infty} -b\,e^{-\lambda b}-\frac{e^{-\lambda b}}{\lambda}+\frac{1}{\lambda}.
\end{align*}\]
Ricordando che
\[
\lim_{b \to +\infty} -b\,e^{-\lambda b}=\lim_{b \to +\infty} -\frac{b}{e^{\lambda b}}=0,
\]
si ottiene infine
\[
\mathbb{E}(X)=\lim_{b \to +\infty} -b\,e^{-\lambda b}-\frac{e^{-\lambda b}}{\lambda}+\frac{1}{\lambda}=0+0+\frac{1}{\lambda}=\frac{1}{\lambda}.
\]
Per una variabile aleatoria \(X\) avente invece distribuzione normale standard \(N(0,1)\), si ha invece
\[\begin{align*}
\mathbb{E}(X)&=\int_{-\infty}^{+\infty} x\,\frac{1}{\sqrt{2 \pi}}\,e^{-\frac12 x^2} \, dx
\\ \\&=\frac{1}{\sqrt{2 \pi}}\int_{-\infty}^{+\infty} x\,e^{-\frac12 x^2} \, dx = \frac{1}{\sqrt{2 \pi}}\left( \int_{-\infty}^{0} x\,e^{-\frac12 x^2} \, dx+\int_{0}^{+\infty} x\,e^{-\frac12 x^2} \, dx\right).
\end{align*}\]
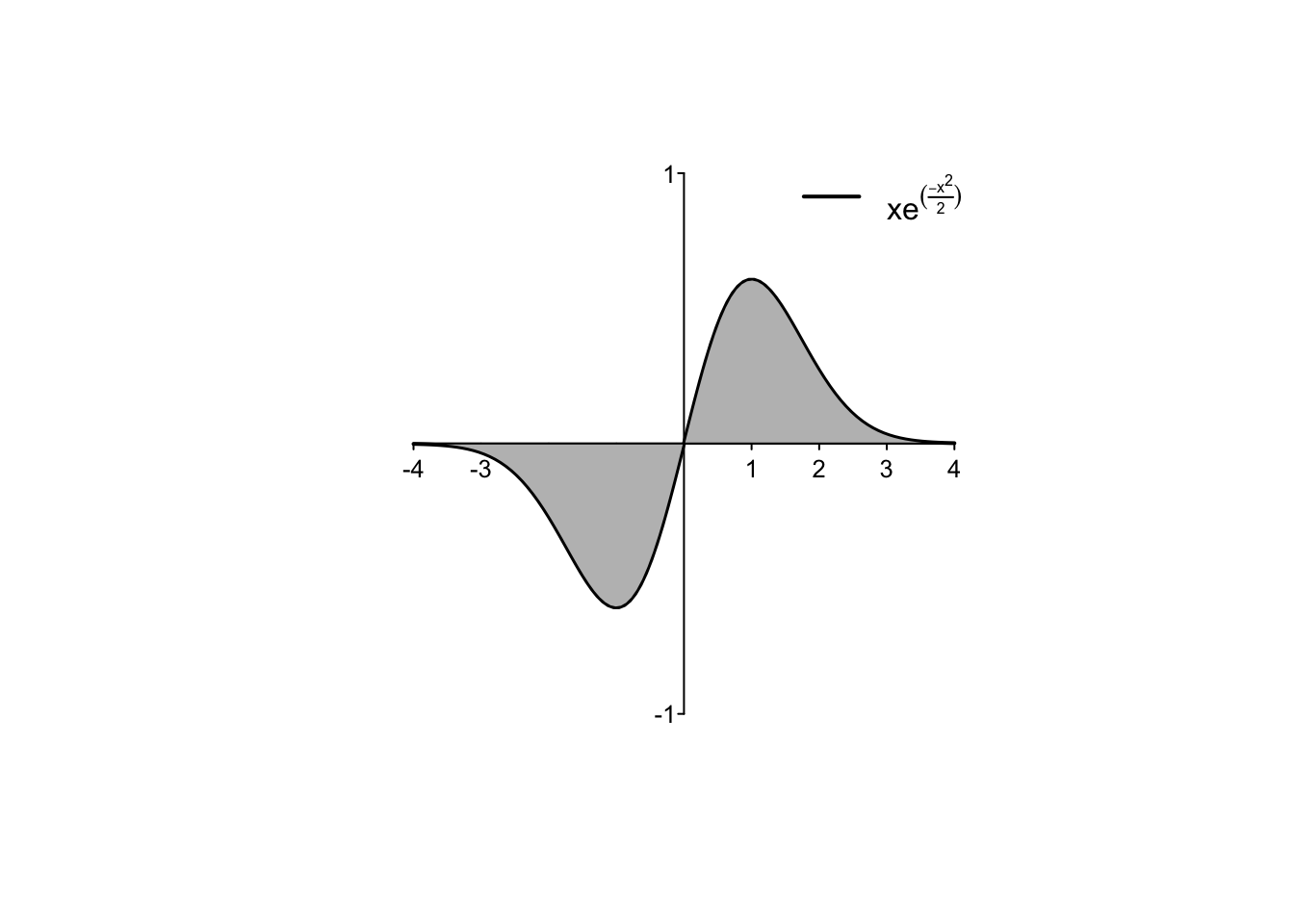
Osservando che la funzione integranda è dispari (il suo grafico è sotto riportato),
e considerando che entrambi gli integrali sono finiti (la funzione integranda si annulla più velocemente di \(\frac{1}{x}\) per \(x \to +\infty\)),
si deduce che
\[
\int_{-\infty}^{0} x\,e^{-\frac12 x^2} \, dx=-\int_{0}^{+\infty} x\,e^{-\frac12 x^2} \, dx\,,
\]
ovvero
\[
\mathbb{E}(X)=0.
\]
La definizione di integrale definito può essere anche estesa ad una funzione integranda che abbia un asintoto verticale ad un estremo dell’intervallo di integrazione.
Example 6.21 Si definisca e si calcoli, al variare di \(k >0\), l’integrale definito
\[
\int_0^{1} \frac{1}{x^k} \,dx.
\]
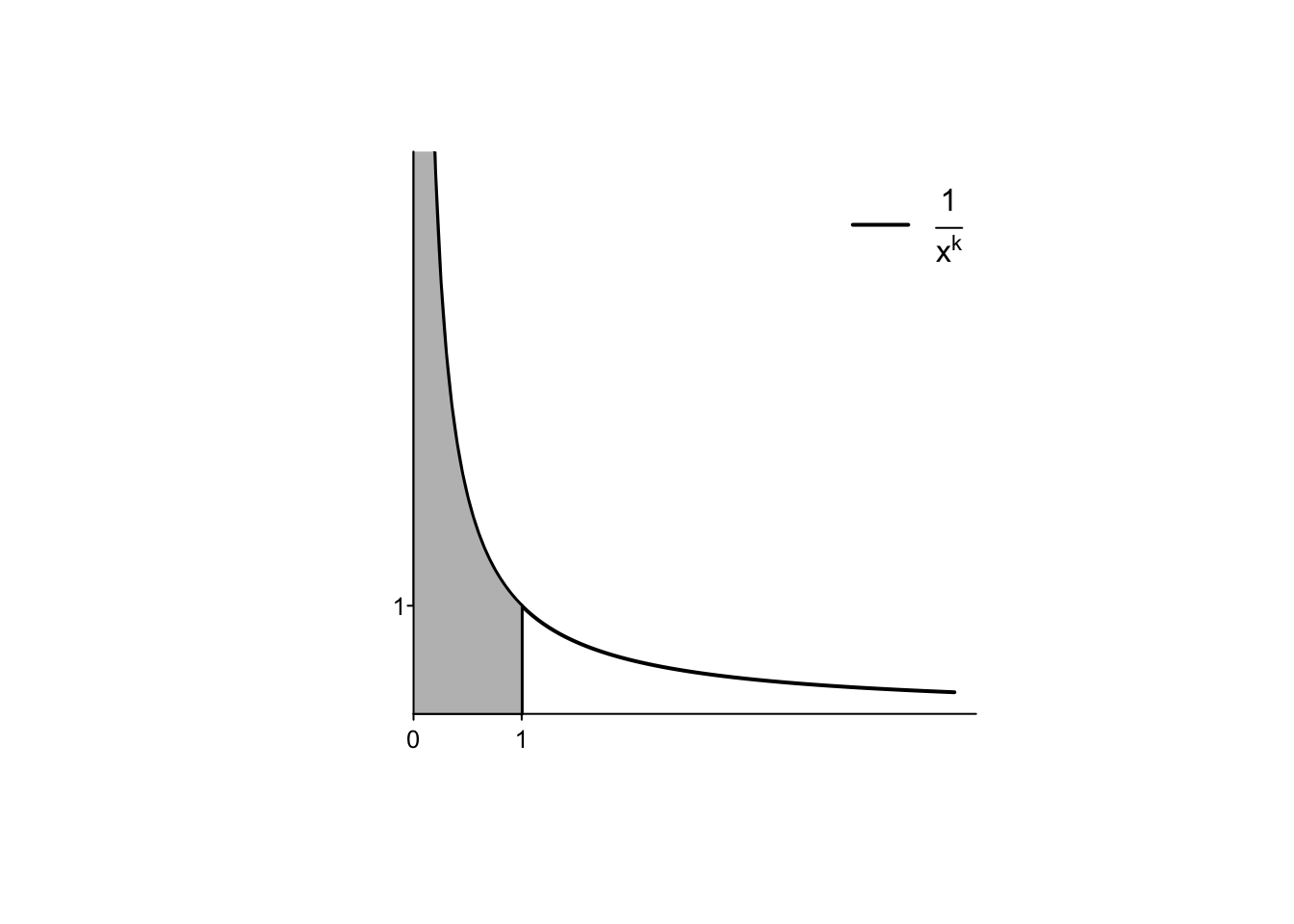La necessità di una nuova definizione deriva dal fatto che la funzione in oggetto non è continua (definita) su \([0,1]\), essendo \(\lim_{x\to 0^+}f(x)=+\infty\).
Dato che si è definito l’integrale su intervallo del tipo \([a,1]\), è naturale porre:
\[
\int_0^{1} \frac{1}{x^k} \,dx = \lim_{a \to 0^+}\,\int_a^{1} \frac{1}{x^k} \,dx,
\]
nel caso in cui questo limite esista, finito o infinito. Se interpretato come l’area nella figura precedente, anche in questo caso l’integrale potrebbe risultare infatti infinito.
Si calcola
\[
\int_a^{1} \frac{1}{x^k} \,dx =\int_a^{1} x^{-k} \,dx =
\begin{cases}
\frac{x^{-k+1}}{-k+1}\Big|_a^1=\frac{1}{1-k}\left( 1-a^{1-k} \right), &\text{ se } k \neq 1; \\ \\
\log(x)\Big|_a^1=-\log a, &\text{ se } k=1.
\end{cases}
\]
Passando al limite per \(a \to 0^+\), si ottiene
\[
\int_a^{1} \frac{1}{x^k} \,dx =
\begin{cases}
\lim_{a \to 0^+}\frac{1}{1-k}\left( 1-a^{1-k} \right)=+\infty, &\text{ se } \,k > 1; \\
\\
\lim_{a \to 0^+}-\log a=+\infty, &\text{ se } \,k=1;\\
\\
\lim_{a \to 0^+}\frac{1}{1-k}\left( 1-a^{1-k} \right)=\frac{1}{1-k}, &\text{ se } \,0<k<1. \\
\end{cases}
\]
Il comportamento dell’integrale in un intorno destro di zero, risulta quindi invertito rispetto a quanto visto per un intorno di \(+\infty\), fermo restando il fatto che la funzione \(f(x)=\frac1x\) risulta essere il punto di demarcazione tra integrali finiti e integrali infiniti.
6.7 Esercizi
Si calcolino i seguenti integrali, cercando di riconoscere immediatamente quale sia il metodo di risoluzione più adatto e conveniente.
Exercise 6.1
Si calcoli \[\int e^x(2x^2-3x+4)\;dx\,\]Exercise 6.2
Si calcoli \[\int \frac{-x^2}{\sqrt{(x^3-4)^3}} \;dx\,\]Exercise 6.3
Si calcoli \[\int \frac{e^{2x}+e^x}{e^x+2} \;dx\,\]Exercise 6.4
Si calcoli \[\int 2x \sqrt{x+5} \;dx\,\]Exercise 6.5
Si calcoli \[\int \frac{e^x}{e^{2x}-3e^x+2} \;dx\,\]Exercise 6.6
Si calcoli \[\int x^5 \sqrt{x^3-5} \;dx\,\]Exercise 6.7
Si calcoli \[\int \frac{e^{2x}-8e^x}{e^x-4} \;dx\,\]Exercise 6.8
Si calcoli \[\int (2x^2-x)\log(x) \;dx\,\]Exercise 6.9
Si calcoli \[\int \frac{\log(x)}{x} \;dx\,\]Exercise 6.10
Si calcoli \[\int \frac{1}{x^2-121} \;dx\,\]Exercise 6.11
Si calcoli \[\int x^7\sqrt{x^4+6} \;dx\,\]Exercise 6.12
Si calcoli \[\int x^5 \, \log(x^5)\;dx\]Exercise 6.13
Si calcoli \[\int x \sqrt{x-2} \;dx\,\]Exercise 6.14
Si calcoli \[\int x \,\sqrt[5]{3x^2-7} \;dx\,\]Exercise 6.15
Si calcoli \[\int \frac{\log(x)}{(\log(x) +2)x} \;dx\,\]Exercise 6.16
Si calcoli \[\int\sqrt[5]{x} \,\log(x) \;dx\,\]Exercise 6.17
Si calcoli \[\int \frac{e^{2x}+3e^x}{e^{2x}+5e^x+6} \;dx\,\]Exercise 6.18
Si calcoli \[\int (2x-3x^3)\log(x) \;dx\,\]Exercise 6.19
Si calcoli \[\int x^3 \log ({x^4}) \;dx\,\]Exercise 6.20
Si calcoli \[\int\frac{5-e^x}{2+e^x} \;dx\,\]Exercise 6.21
Si calcoli \[\int \frac{3}{2-e^x} \;dx\,\]Exercise 6.22
Si calcoli \[\int \frac{e^x+e^{2x}}{4+e^x} \;dx\,\]Exercise 6.23
Si calcoli \[\int e^{x}(3x^2-2x) \;dx\,\]Exercise 6.24
Si calcoli \[\int \frac{x^3}{\sqrt[3]{(8+x^4)^5}} \;dx\,\]Exercise 6.25
Si calcoli \[\int \frac{e^x(1-e^{2x})}{1+e^x} \;dx\,\]Exercise 6.26
Si calcoli \[\int 3x^2 \log(x^2) \;dx\,\]Exercise 6.27
Si calcoli \[\int (2x^2+3)e^x \;dx\,\]Exercise 6.28
Si calcoli \[\int \frac{e^x}{e^{2x}-1} \;dx\,\]Exercise 6.29
Si calcoli \[\int \frac{4x}{\sqrt{3x^2-1}} \;dx\,\]Exercise 6.30
Si calcoli \[\int \frac{5}{x^2+x-2} \;dx\,\]Exercise 6.31
Si calcoli \[\int \frac{4e^x}{e^{2x}-e^x-2} \;dx\,\]