4 Derivate

La derivata di una funzione, quando esiste, fornisce informazioni sulla sua monotonia. Al contrario del calcolo dei limiti (che si deve ricondurre ad una casistica), il calcolo della derivata di una qualsiasi funzione ottenuta a partire da funzioni elementari è una operazione meccanica, basata sulla applicazione delle semplici regole che questo capitolo descrive.

4.1 Definizione di derivata

Si consideri la retta passante per i due punti \((x,f(x))\) e \((x+h, f(x+h))\) sul grafico di una arbitraria funzione reale \(f\). Il coefficiente angolare di questa retta è dato dal cosiddetto \[ \frac{f(x+h)-f(x)}{x+h-x}=\frac{f(x+h)-f(x)}{h}, \quad h \neq 0. \]

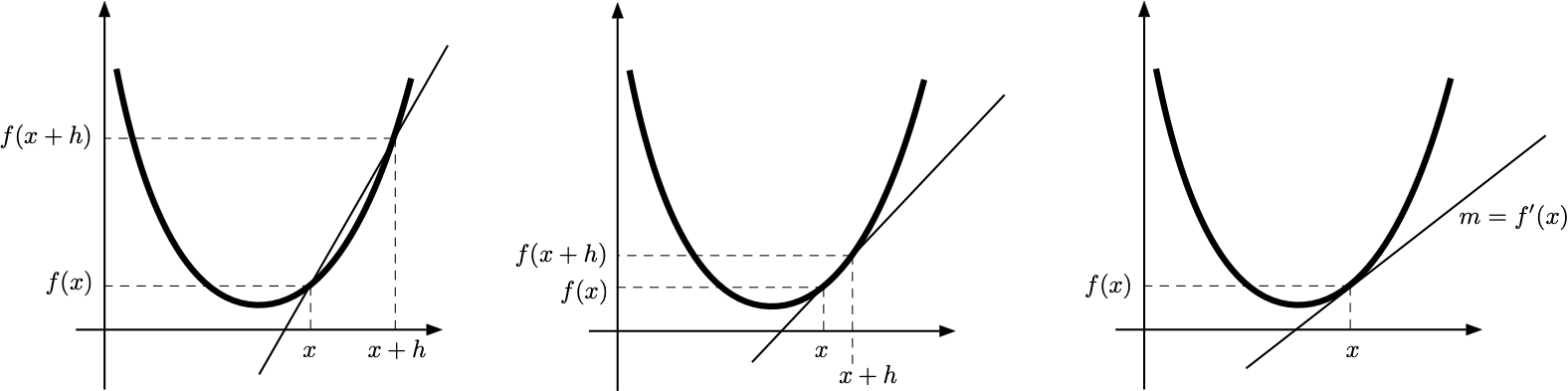
Come è illustrato in figura, se si fa avvicinare il secondo punto al primo la retta che passa per i due punti si avvicina ad essere la tangente al grafico della funzione nel punto \((x,f(x))\). Il coefficiente angolare di questa retta non può essere definito dalla formula precedente (che non vale nel caso i due punti coincidano, ovvero per \(h=0\)), ma prende il nome di derivata della funzione.

Definition 4.1 Una funzione \(f:A \subseteq \mathbb{R}\to \mathbb{R}\) si dice derivabile nel punto interno \(x \in A\) se esiste finito \[ f'(x)=\lim_{h \to 0 } \,\frac{f(x+h)-f(x)}{h}. \] In tal caso, questo limite è detto derivata della funzione \(f\) nel punto \(x\).

Se \(f\) è derivabile per ogni \(x \in A\), con \(A\) aperto, si dice che \(f\) è derivabile su \(A\) e si definisce la funzione derivata \(f':A \subseteq \mathbb{R} \to \mathbb{R},\, x \to f'(x)\), che associa ad ogni punto la derivata della funzione in quel punto.

Remark. Osserviamo i seguenti punti fondamentali sulla definizione di derivata:

non potendosi calcolare il rapporto incrementale per \(h=0\), si definisce derivata il limite (se esiste) del rapporto incrementale per \(h \to 0\);
da questo segue che, quando esiste, la derivata di una funzione in un punto è il coefficiente angolare della retta tangente al grafico della funzione in quel punto. Ricordando la formula della retta passante per il punto di coordinate \((x_0,f(x_0))\) e avente coefficiente angolare \(f'(x_0)\), si ha che l’equazione della retta tangente al grafico di una funzione derivabile in un punto \(x=x_0\) è data da \[ y=f'(x_0)(x-x_0)+f(x_0)=f'(x_0)\,x-f'(x_0)x_0+f(x_0); \]
la definizione richiede che il punto \(x\) sia interno al dominio della funzione di modo che si possa trovare un intorno \(I(x) \subseteq A\) in cui calcolare il limite del rapporto incrementale. Si ricordi che se \(A\) è aperto, allora tutti i suoi punti sono interni;
usando nella definizione il limite sinistro (\(h \to 0^-\)) o il limite destro (\(h \to 0^+\)), si definiscono i concetti di derivata sinistra \(f'_{-}(x)\) o derivata destra \(f'_{+}(x)\) di \(f\) nel punto \(x\). Una funzione è quindi derivabile in un punto se e solo se esistono finite sia la sua derivata sinistra che la sua derivata destra in quel punto, ed esse coincidono;
la derivata della funzione in un punto, \(f'(x)\), è un numero reale. La derivata \(f'\) è quella funzione che ad ogni valore della \(x\) associa il valore della derivata calcolata in quel punto;
quando si ha \[ \lim_{h \to 0} \left| \frac{f(x+h)-f(x)}{h} \right|=+\infty, \] si parla comunemente di derivata infinita, con ciò comunque intendendo che la funzione non è derivabile in \(x\);
è possibile definire una funzione derivabile su un intervallo chiuso \([a,b]\), e di conseguenza la sua funzione derivata \(f'\) su \([a,b]\) con ciò intendendo che in \(x=a\) esiste (solo) la derivata destra e in \(x=b\) esiste (solo) la derivata sinistra.

È immediato dimostrare che la derivabilità è una condizione più forte della continuità: una funzione derivabile è anche continua.

Theorem 4.1 Se \(f\) è derivabile in \(x=x_0\), allora \(f\) è continua in \(x=x_0\).

Proof. Per definizione, se \(f\) è derivabile in \(x=x_0\) si ha che \[ \lim_{h \to 0 } \,\frac{f(x_0+h)-f(x_0)}{h}=f'(x_0) \in \mathbb{R}. \] In questo limite, il numeratore del rapporto incrementale deve tendere a 0, altrimenti diviso per un denominatore \(h\) che tende a zero non potrebbe restituire un limite finito. Si ha dunque che \[ \lim_{h \to 0 } f(x_0+h)-f(x_0)= 0 \quad \Rightarrow \quad \lim_{h \to 0 } f(x_0+h)=f(x_0). \] Ponendo \(x=x_0+h\), si ha dunque che \(\lim_{x \to x_0} f(x)=f(x_0),\) pertanto la funzione è continua in \(x=x_0\).

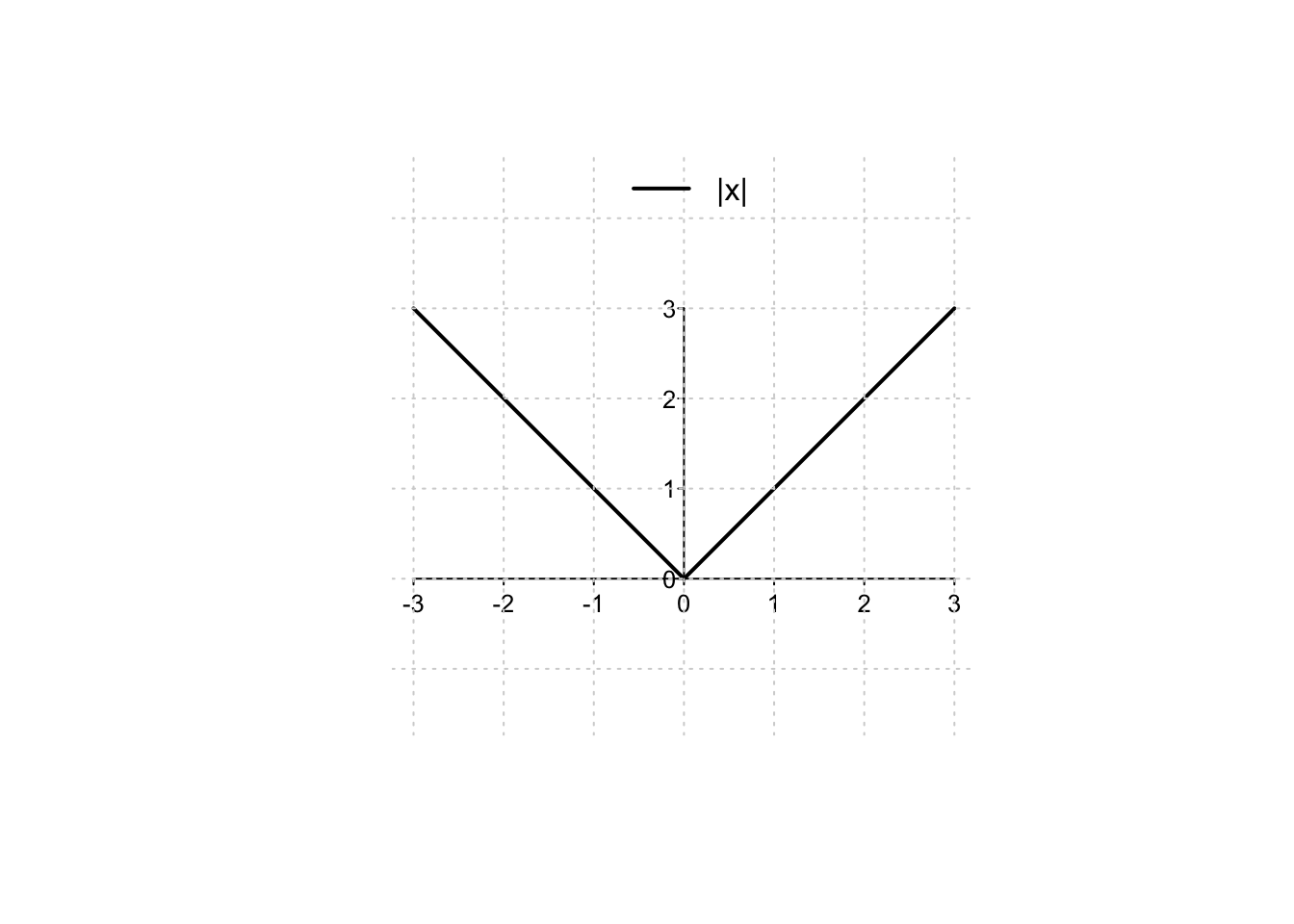
Se una funzione derivabile è anche continua, non è vero il viceversa: il valore assoluto è il classico esempio di funzione continua che possiede un punto di non derivabilità.

Example 4.1 Si consideri la funzione \(f:\mathbb{R} \to \mathbb{R}, f(x)=|x|\). È immediato verificare che in un intorno di \(x=0\) si ha \[\begin{align*} f'_{+}(0)=&\lim_{h \to 0^+}\,\frac{f(0+h)-f(0)}{h}=\lim_{h \to 0^+}\,\frac{|h|-0}{h}=\lim_{h \to 0^+}\,\frac{h}{h}=1, \\ f'_{-}(0)=&\lim_{h \to 0^-}\,\frac{f(0+h)-f(0)}{h}=\lim_{h \to 0^-}\,\frac{|h|-0}{h}=\lim_{h \to 0^-}\,\frac{-h}{h}=-1. \end{align*}\] Avendo derivata sinistra e derivata destra differenti, la funzione non è derivabile in \(x=0\), pur essendo ivi continua. Dai calcoli precedenti si deduce inoltre che, per \(x>0\), si ha \(f(x)=x\) e \(f'(x)=1\); per \(x<0\) si ha \(f(x)=-x\) e \(f'(x)=-1\).

Quando una funzione possiede in un punto derivata sinistra e derivata destra differenti, si dice che il suo grafico ha un punto angoloso. Osservando il grafico del valore assoluto, ben si capisce questa nomenclatura.

4.2 Derivata delle funzioni potenza

Negli esempi seguenti, si utilizza la definizione per calcolare la derivata di alcune funzioni elementari.

Example 4.2 Una funzione lineare \(f(x)=mx+q\), \(m,q \in \mathbb{R}\) è derivabile su tutto l’asse reale. Si calcola infatti \[\begin{align*} f'(x)=\lim_{h \to 0}\,\frac{f(x+h)-f(x)}{h}&=\lim_{h \to 0}\,\frac{m(x+h)+q-(mx+q)}{h}\\&=\lim_{h \to 0} \,\frac{mx+mh+q-mx-q}{h}= \lim_{h \to 0} \, \frac{m \; h}{h}=m. \end{align*}\] Questo risultato è pienamente coerente con il fatto che la retta tangente ad una retta è la retta stessa, quindi la sua derivata è pari al suo coefficiente angolare.

Ponendo \(m=0\) si deduce anche che la funzione costante \(f(x)=q\) ha derivata nulla \(f'(x)=0, \, x \in \mathbb{R}\).

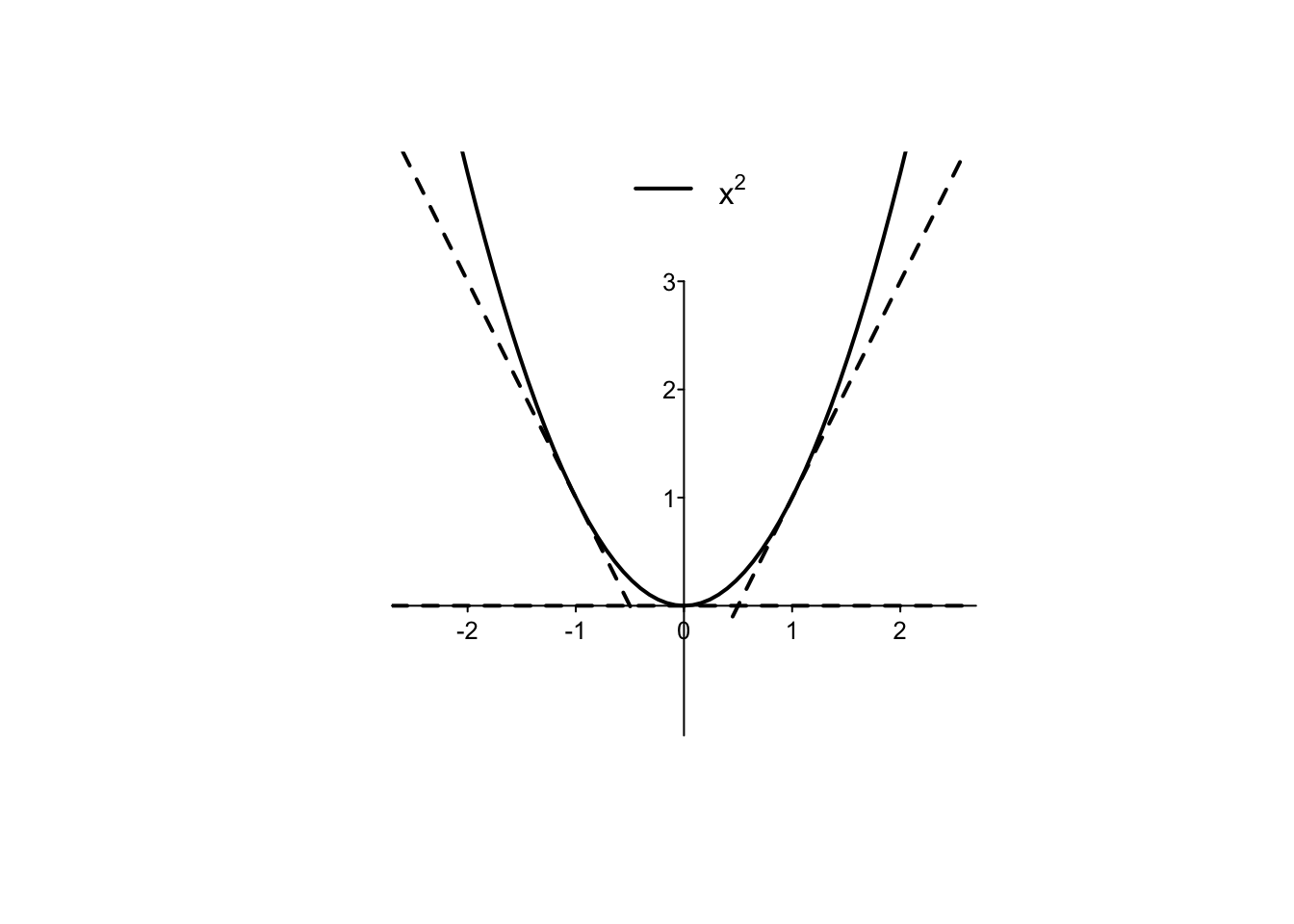
Example 4.3 La funzione quadrato \(f(x)=x^2\) è derivabile su tutto l’asse reale. Si calcola \[\begin{align*} f'(x)&=\lim_{h \to 0}\,\frac{f(x+h)-f(x)}{h}=\lim_{h \to 0}\,\frac{(x+h)^2-x^2}{h}\\&=\lim_{h \to 0} \,\frac{x^2+2xh+h^2-x^2}{h}=\lim_{h \to 0} \, \frac{h\,(2x+h)}{h}=\lim_{h \to 0} (2x+h)=2x. \end{align*}\] Nella figura seguente, si possono verificare i valori della derivata (coefficiente angolare della retta tangente al grafico) della parabola: \(f'(-1)=-2,f'(0)=0,f'(1)=2\).

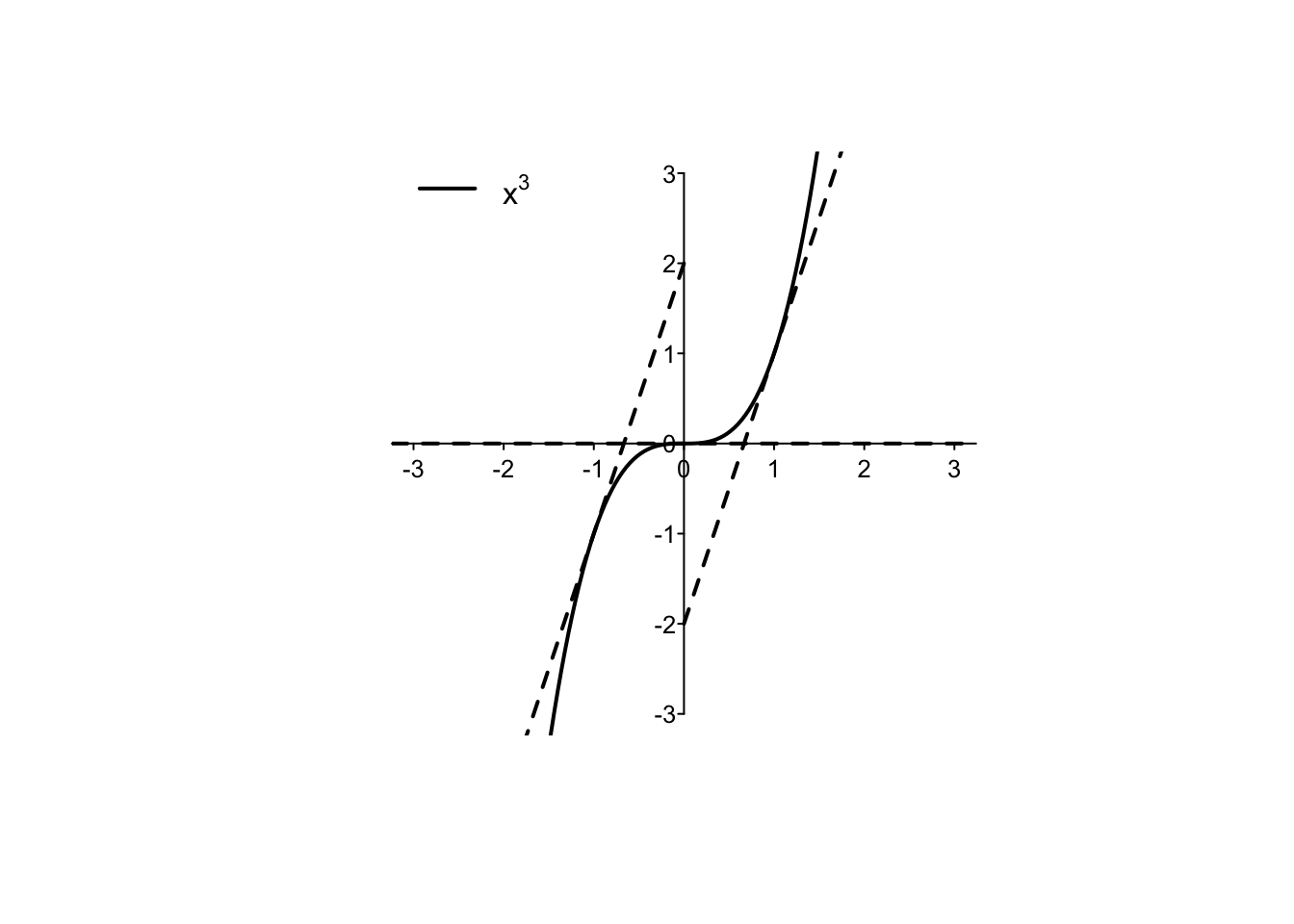
Example 4.4 La funzione cubo \(f(x)=x^3\) è derivabile su tutto l’asse reale. Si calcola \[\begin{align*} f'(x)&=\lim_{h \to 0}\,\frac{f(x+h)-f(x)}{h}\\&=\lim_{h \to 0}\,\frac{(x+h)^3-x^3}{h}=\lim_{h \to 0} \,\frac{x^3+3x^2h+3xh^2+h^3-x^3}{h}\\&=\lim_{h \to 0} \, \frac{h\,(3x^2+3xh+h^2)}{h}=\lim_{h \to 0} (3x^2+3xh+h^2)=3x^2. \end{align*}\] Nella figura seguente, si possono verificare i valori: \(f'(-1)=3\), \(f'(0)=0,f'(1)=3\). Si osservi come la derivata della funzione cubo sia non negativa: \(f'(x)=3x^2 \geq 0, x \in \mathbb{R}.\)

Gli esempi precedenti sono propedeutici al seguente Teorema.

Theorem 4.2 Per \(n \in \mathbb{N}\), la funzione potenza \(f(x)=x^n\) è derivabile su tutto l’asse reale e vale la seguente regola. \[ \textbf{Derivata di una potenza naturale:} \quad \boldsymbol{\left( x^n \right)' = n x^{n-1}}. \]

Proof. Dalla definizione di derivata si ottiene \[\begin{align*} f'(x)=\lim_{h \to 0}\,\frac{f(x+h)-f(x)}{h}=\lim_{h \to 0}\,\frac{(x+h)^n-x^n}{h}. \end{align*}\] In \((x+h)^n\) si moltiplica il fattore \((x+h)\) per se stesso \(n\) volte, ovvero si sommano tra di loro tutti i possibili prodotti ottenuti prendendo \(n\) volte o una \(x\) o una \(h\). Se si scelgono tutte le \(x\) si ottiene \(x^n\). Se si moltiplicano tra loro tutte le \(x\) tranne una, al posto della quale si sceglie una \(h\), si ottiene \(x^{n-1}h\), e questo si può fare in \(n\) modi diversi a seconda dal quale degli \(n\) fattori si prenda la \(h\). Si avrà quindi che \[ (x+h)^n=(x+h)\cdot(x+h)\cdot \ldots \cdot (x+h)=x^n+nx^{n-1}h+R(h), \] dove il fattore \(R(h)\) contiene sempre potenze \(h^k\) con \(k \geq 2\) (ad esempio contiene \(h^n\)), eventualmente moltiplicate per una costante che dipende da \(n\). Ricordando gli esempi precedenti, si ottiene \[\begin{align*} f'(x)&=\lim_{h \to 0}\,\frac{f(x+h)-f(x)}{h}\\&=\lim_{h \to 0}\,\frac{(x+h)^n-x^n}{h} =\lim_{h \to 0}\,\frac{x^n+nx^{n-1}h+R(h)-x^n}{h} \\&=\lim_{h \to 0}\,\frac{nx^{n-1}h+R(h)}{h}=\lim_{h \to 0}\,nx^{n-1}+\frac{R(h)}{h}=nx^{n-1}. \end{align*}\] Si osservi che questo risultato include i casi trattati negli Esempi precedenti.

Al contrario delle potenze naturali, le potenze frazionarie (radici) presentano tipicamente punti di non derivabilità.

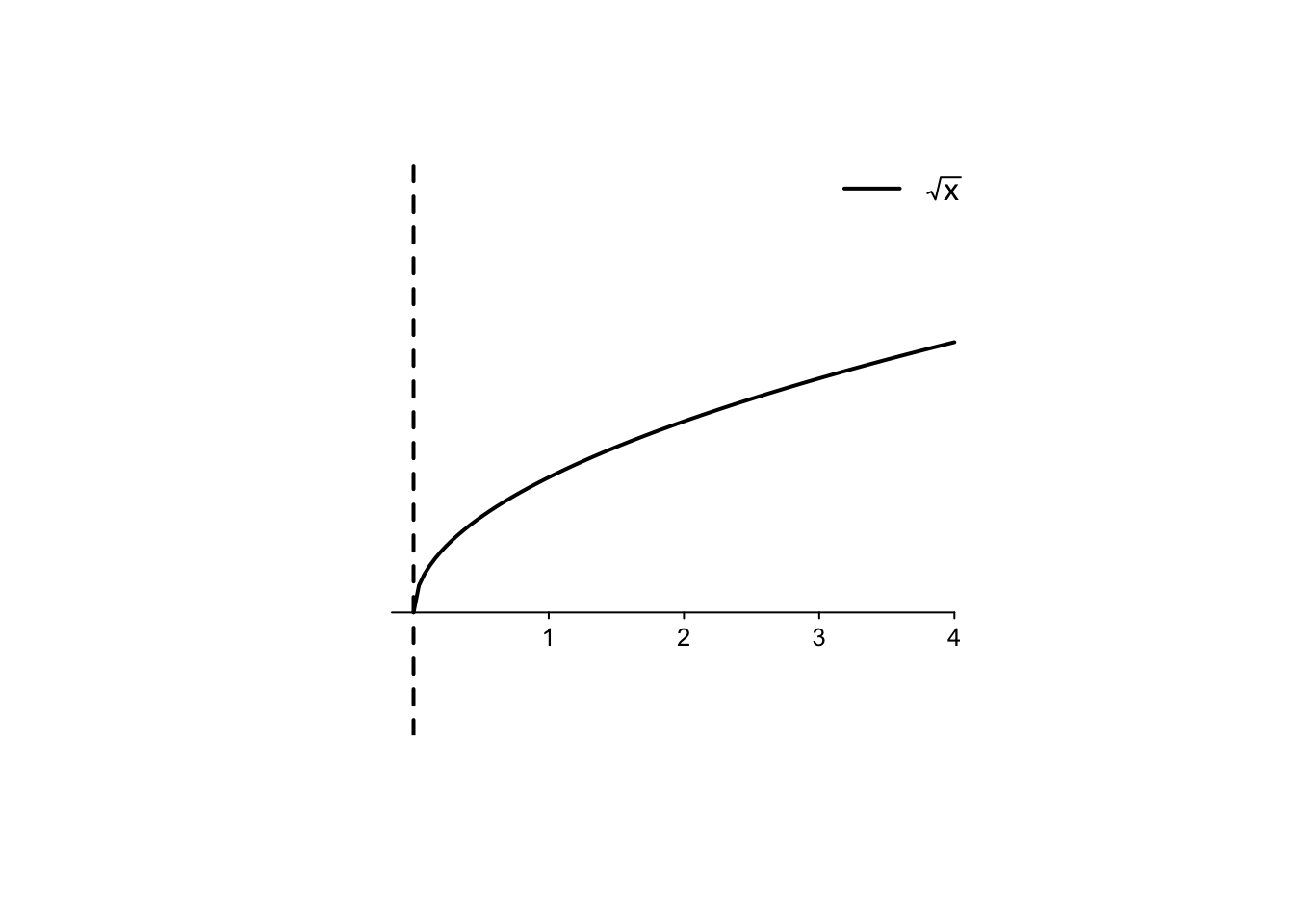
Example 4.5 Si consideri la funzione \(f:[0,+\infty) \to \mathbb{R}, f(x)=\sqrt{x}\). Per \(x>0\), si ottiene \[\begin{align*} f'(x)=&\lim_{h \to 0}\,\frac{f(x+h)-f(x)}{h}=\lim_{h \to 0}\,\frac{\sqrt{x+h}-\sqrt{x}}{h} \\=&\lim_{h \to 0}\,\frac{(\sqrt{x+h}-\sqrt{x})}{h}\frac{(\sqrt{x+h}+\sqrt{x})}{(\sqrt{x+h}+\sqrt{x})} \\=&\lim_{h \to 0}\,\frac{x+h-x}{h(\sqrt{x+h}+\sqrt{x})}=\lim_{h \to 0}\,\frac{h}{h(\sqrt{x+h}+\sqrt{x})}= \lim_{h \to 0}\,\frac{1}{(\sqrt{x+h}+\sqrt{x})}=\frac{1}{2\sqrt{x}}. \end{align*}\] Dato che nel dominio naturale della radice quadrata è contenuto solo un intorno destro di \(x=0\), in tale punto si può calcolare solamente la derivata destra, ovvero \[\begin{align*} f'_{+}(0)=\lim_{h \to 0^+}\,\frac{f(0+h)-f(0)}{h}=\lim_{h \to 0^+}\,\frac{\sqrt{h}-0}{h}=\lim_{h \to 0^+}\,\frac{h^{\frac{1}{2}}}{h}=\lim_{h \to 0^+}\,\frac{1}{h^{\frac{1}{2}}}=+\infty. \end{align*}\] La funzione radice quadrata quindi nascerà in zero con una derivata infinita, ovvero con una tangente verticale, come si può osservare dal suo grafico. Questo è il tipico comportamento delle radici quadrate nei punti in cui si annullano.

Example 4.6 È possibile ampliare il dominio naturale di una radice quadrata ponendo il suo argomento dentro un valore assoluto. In questo caso, la funzione \(f:\mathbb{R} \to \mathbb{R}, f(x)=\sqrt{|x|}\) è una funzione pari e il suo grafico sarà simmetrico rispetto all’asse delle ordinate.

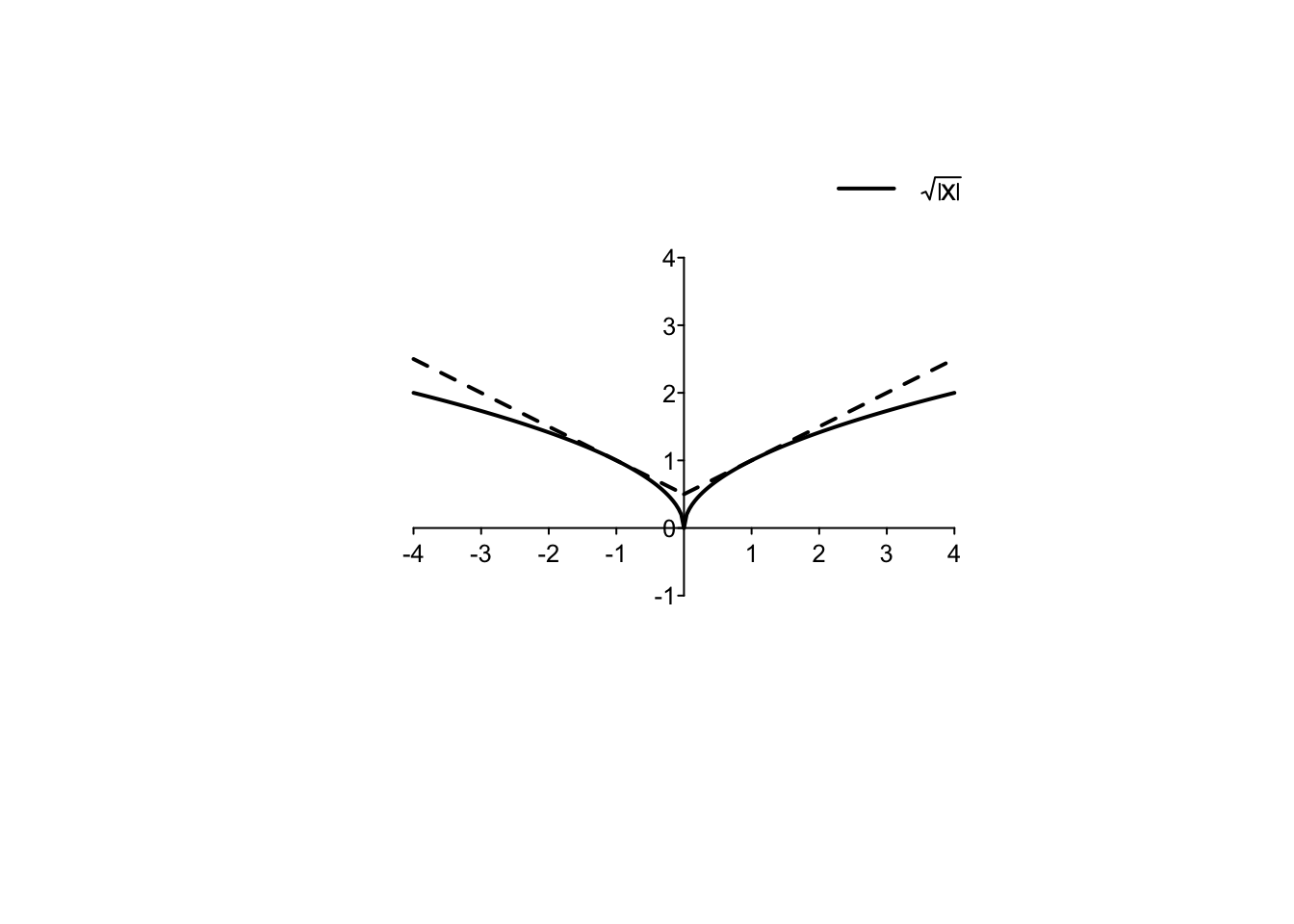
Dal grafico di \(\sqrt{|x|}\) si possono dedurre due importanti osservazioni:

In \(x=0\), la derivata sinistra è pari a \(-\infty\), la derivata destra è pari a \(+\infty\). In questi casi si dice che il grafico della funzione ha una cuspide;
la funzione è derivabile per tutti gli \(x<0\), e con calcoli analoghi all’Esempio 4.5 si ottiene che \[ f'(x)= -\frac{1}{2\sqrt{-x}},\quad x <0. \] Si osservi ad esempio nel grafico che \(f(-1)=-\frac{1}{2}=-f(1)\).

Anche per la radice quadrata \(f(x)=x^{1/2}\) vale, nei punti interni al suo dominio naturale, la regola vista per le potenze intere, ovvero che \[ \left(x^{\frac{1}{2}}\right)'= \frac{1}{2} x^{\left(\frac{1}{2}-1\right)}=\frac{1}{2}x^{-\frac{1}{2}}=\frac{1}{2\sqrt{x}}, \quad x >0. \] Si può dimostrare infatti che la regola di derivazione per le potenze vale anche per \(x^{\frac{m}{n}}, \,m,n \in \mathbb{N}, \,n \neq 0\), per \(x>0\).

Nel caso della radice cubica, si può calcolare la derivata su tutta la retta reale.

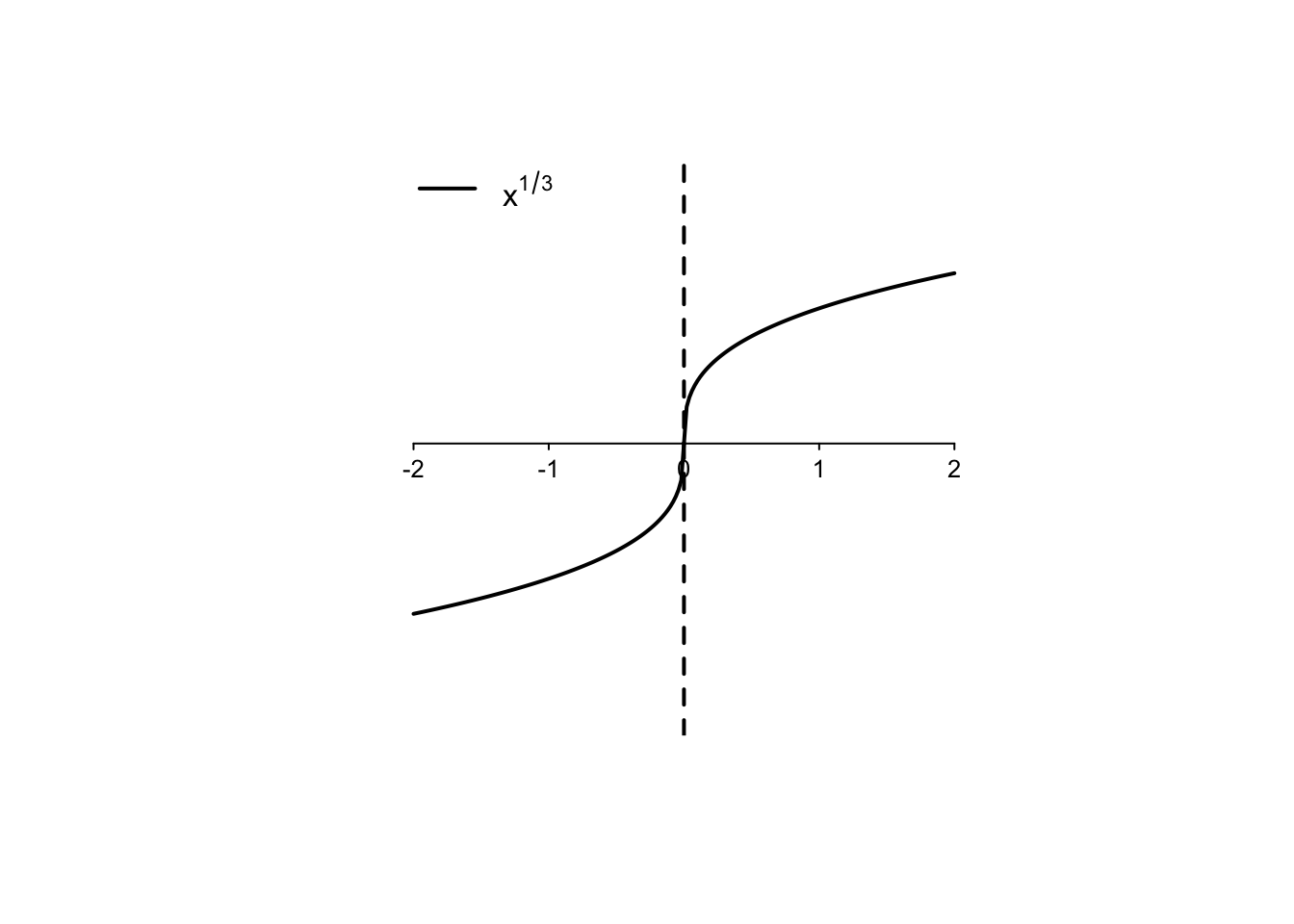
Example 4.7 Si consideri la funzione radice cubica \(f:\mathbb{R}\to \mathbb{R}, f(x)=\sqrt[3]{x}=x^{\frac{1}{3}}\). È possibile dimostrare (con calcoli lunghi ma elementari) che si ottiene \[ \left(x^{\frac{1}{3}}\right)'= \frac{1}{3} x^{\left(\frac{1}{3}-1\right)}=\frac{1}{3}x^{-\frac{2}{3}}=\frac{1}{3\sqrt[3]{x^2}}, \quad x \neq 0. \] Per quanto riguarda il punto \(x=0\), si può calcolare la derivata attraverso la definizione. \[\begin{align*} f'(0)=&\lim_{h \to 0}\,\frac{f(0+h)-f(0)}{h}=\lim_{h \to 0}\,\frac{\sqrt[3]{0+h}-0}{h} \\=&\lim_{h \to 0}\,\frac{\sqrt[3]{h}}{h}=\lim_{h \to 0}\,\frac{h^{\frac{1}{3}}}{h}=\lim_{h \to 0}\, h^{-\frac{2}{3}}=\lim_{h \to 0}\,\frac{1}{h^{\frac{2}{3}}}=\lim_{h \to 0}\,\frac{1}{\sqrt[3]{h^2}}=+\infty. \end{align*}\] La funzione radice cubica quindi interseca l’origine degli assi con una derivata infinita, ovvero con una tangente verticale, come si può osservare dal suo grafico. Questo è il tipico comportamento delle radici cubiche nei punti in cui si annullano. Si osservi ancora che, anche se si può parlare di derivata infinita della funzione cubica in \(x=0\), la funzione in questo punto non è derivabile.

4.3 Derivata della funzione logaritmo

Ricordando la definizione di logaritmo data nel Capitolo 2, si dimostra il seguente teorema.

Theorem 4.3 La funzione logaritmo \(f(x)=\log (x)\) è derivabile sul suo dominio naturale e vale la seguente regola. \[ \textbf{Derivata del logaritmo:} \quad \boldsymbol{\left( \log (x) \right)' = \frac{1}{x}, \quad x>0}. \]

Proof. Dalla definizione della funzione \(f:(0,+\infty) \to \mathbb{R}, f(x)=\log{x}\) data nel Capitolo 2, si ha che il valore \(\log(x+h)-\log(x)\), per \(h>0\), è il valore dell’area compresa sopra l’asse delle ascisse, e sotto il grafico della funzione \(\frac{1}{x}\), tra i punti \(x\) e \(x+h\). Dato che la funzione \(\frac{1}{x}, x >0,\) è decrescente, quest’area è compresa tra quella dei due rettangoli nella figura seguente. Si avrà dunque che \[ h \frac{1}{x+h} < \log(x+h)-\log(x) < h \frac{1}{x}, \] ovvero, dividendo per \(h>0\), che \[ \frac{1}{x+h} < \frac{\log(x+h)-\log(x)}{h} < \frac{1}{x}. \] Calcolando il limite in un intorno destro di \(h=0\), si ottiene perciò \[ \frac{1}{x}=\lim_{h \to 0^+} \frac{1}{x+h} < \lim_{h \to 0^+} \frac{\log(x+h)-\log(x)}{h} < \lim_{h \to 0^+} \frac{1}{x}=\frac{1}{x}. \] Da un analogo ragionamento per \(h<0\), si deduce che \(f'(x)=\frac{1}{x}\).

4.4 Regole di derivazione

Attraverso semplici regole di derivazione, si può calcolare la derivata di qualsiasi funzione derivabile ottenuta tramite somma, prodotto, quoziente e composizione di funzioni elementari. Le dimostrazioni delle seguenti regole, espresse sotto forma di Teoremi, sono elementari ma a volte laboriose. In particolare, la regole della derivata della somma e del prodotto per una costante discendono immediatamente dalla definizione di derivata e dalle proprietà dei limiti (si ricordi che la derivata altro non è che un limite).

Theorem 4.4 Date due funzioni \(f,g:A\subseteq \mathbb{R} \to \mathbb{R}\) derivabili con derivate \(f'\) e \(g'\), la loro somma \(f+g\) è derivabile e vale la seguente regola. \[ \textbf{Derivata della somma:} \quad \boldsymbol{\left( f + g \right)'(x) = f'(x)+g'(x)}. \] \[ \textbf{Derivata del prodotto per una costante:} \quad \boldsymbol{\left(\lambda \, f \right)'(x) = \lambda \,f'(x)}. \]

Si legga con attenzione la scrittura usata per la derivata della somma: la funzione derivata della somma delle funzioni \(f\) e \(g\), calcolata nel punto \(x\), è uguale alla somma della derivata di \(f\) calcolata nel punto \(x\) e della derivata di \(g\) calcolata nel punto \(x\).

La regola di derivazione della somma ci permette di calcolare la derivata di qualsiasi polinomio.

Example 4.8 Si calcoli la derivata della funzione \(f:\mathbb{R} \to \mathbb{R}\), \[f(x)=4x^5-3x^4+2x-5, \quad\text{ nel punto } \quad x=1.\] Sfruttando la regola di derivazione delle potenze, si ha che \[f'(x)= 20 x^4 - 12 x^3+2,\quad \text{ da cui }\quad f'(1)=10.\]

La derivata di un polinomio di grado \(n\) è un polinomio di grado \(n-1\).

Quando si vuole trovare la derivata di una funzione in un punto \(x=x_0\) sfruttando le regole di derivazione, si calcola prima la funzione derivata \(f'(x)\), quindi si sostituisce il punto in oggetto ottenendo il valore \(f'(x_0)\).

Theorem 4.5 Date due funzioni \(f,g:A\subseteq \mathbb{R} \to \mathbb{R}\) derivabili con derivate \(f'\) e \(g'\), il loro prodotto \(f\cdot g\) è derivabile e vale la seguente regola. \[ \textbf{Derivata del prodotto:} \quad \boldsymbol{\left( f \cdot g \right)'(x) = f'(x)g(x) + f(x)g'(x)}. \]

Example 4.9 Si calcoli la derivata della funzione \(f:(0,+\infty) \to \mathbb{R}\), \[f(x)=x(\log(x) -1), \quad\text{ nel punto } \quad x=1.\] Sfruttando la regola di derivazione del prodotto, si ha che \[f'(x)= (x)'(\log(x)-1) + x (\log(x)-1)'= 1 \cdot (\log (x)-1)+x \frac{1}{x}= \log(x)-1+1=\log(x),\] da cui \(f'(1)=0\).

Theorem 4.6 Date due funzioni \(f,g:A\subseteq \mathbb{R} \to \mathbb{R}\), \(g(x) \neq 0, \; x \in A\), derivabili con derivate \(f'\) e \(g'\), il loro quoziente \(f/g\) è derivabile e vale la seguente regola. \[ \textbf{Derivata del quoziente:} \quad \boldsymbol{\left( \frac{f}{g} \right)'(x) = \frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2}}. \]

Mediante la regola di derivazione del quoziente, si può calcolare la derivata delle potenze negative.

Example 4.10 Si trovi la derivata della funzione \(f:(0,+\infty) \to \mathbb{R}, f(x)=x^{-\frac{m}{n}}\), \(m,n \in \mathbb{N},\, n \neq 0.\) Si ottiene \[ \left(x^{-\frac{m}{n}}\right)'=\left(\frac{1}{x^{\frac{m}{n}}}\right)'=\frac{-\frac{m}{n}x^{\left(\frac{m}{n}-1\right)}}{x^{\frac{2m}{n}}}=-\frac{m}{n}x^{\left(\frac{m}{n}-1-2\frac{m}{n}\right)}=-\frac{m}{n}x^{\left(-\frac{m}{n}-1\right)}. \] Si osserva quindi come la formula già vista per le potenze positive valga identicamente anche per le potenze negative, nel loro dominio naturale.

Example 4.11 Calcolare la derivata della funzione
\[ f:(0,+\infty) \to \mathbb{R}, f(x)=\frac{1}{x}-\sqrt{x}, \quad \text{ nel punto } \quad x=1. \] Al fine di calcolare più agevolmente la derivata, è conveniente scrivere la funzione come \(f(x)=x^{-1}-x^{\frac{1}{2}}\). Sfruttando la regola di derivazione delle potenze, si ottiene \[ f'(x)= -x^{-2}-\left(\frac{1}{2}x^{-\frac{1}{2}}\right)=-\frac{1}{x^2}-\frac{1}{2\sqrt{x}},\quad \text{ da cui }\quad f'(1)=-\frac{3}{2}. \]

Una derivata di frequente utilizzo da tenere sempre a mente è \[\left(\frac{1}{x}\right)'=-\frac{1}{x^2}.\]

Example 4.12 Calcolare la derivata della funzione \[ f:(0,+\infty) \to \mathbb{R},\, f(x)=\frac{x+1}{\sqrt{x}}. \] Usando la regola di derivazione del quoziente si ottiene \[\begin{align*} \left(\frac{x+1}{x^{\frac12}}\right)'&= \frac{ (x+1)'x^{\frac12}-(x+1)\left(x^{\frac{1}{2}}\right)'}{\left(x^{\frac12}\right)^2} \\&=\frac{x^{\frac12}-(x+1)\frac{1}{2}x^{-\frac{1}{2}}}{x}=x^{-\frac12}-\frac12(x+1)x^{-\frac32} \\&=x^{-\frac32}\left(x-\frac12(x+1)\right)=x^{-\frac32}\frac12(x-1)=\frac{x-1}{2x^{\frac32}}. \end{align*}\] Si osservi che in questo caso è più agevole calcolare la derivata semplicemente come \[\begin{align*} \left(\frac{x+1}{\sqrt{x}}\right)'=&\left(\frac{x}{\sqrt{x}}+\frac{1}{\sqrt{x}} \right)'=\left(\frac{x}{\sqrt{x}}\right)' +\left(\frac{1}{\sqrt{x}} \right)'\\=&\left(x^{\frac12}\right)' +\left(x^{-\frac12}\right)'=\frac12x^{-\frac12}-\frac12x^{-\frac32}=\frac12x^{-\frac32}\left(x-1 \right)=\frac{x-1}{2x^{\frac32}}. \end{align*}\] Si osservi inoltre che la funzione \(f\) non è derivabile nell’intorno destro di \(x=0\).

Non si deve mai prediligere l’utilizzo di una formula meccanica (come quella della derivata del quoziente) quando si può ottenere lo stesso risultato con meno calcoli e quindi minore probabilità di errore.

Theorem 4.7 Date due funzioni derivabili \(f:A \to \mathbb{R}\) e \(g: B \to \mathbb{R}\) con \(f(A) \subseteq B\), la loro composizione \((g \circ f):A \to \mathbb{R}\) è derivabile e vale la seguente regola. \[ \textbf{Derivata della composizione:} \quad \boldsymbol{\left( g \circ f \right)'(x) = g'(f(x)) \cdot f'(x)}. \]

La formula della derivata della composizione ci permette di calcolare la derivata della funzione esponenziale.

Theorem 4.8 La funzione esponenziale \(f(x)=e^x\) è derivabile sul suo dominio naturale e vale la seguente regola. \[ \textbf{Derivata dell'esponenziale:} \quad \boldsymbol{\left( e^x \right)' = e^x, \quad x\in\mathbb{R}}. \]

Proof. Dato che l’esponenziale è la funzione inversa del logaritmo si ha che \[ x=\log(e^x), \; x \in \mathbb{R}. \] Derivando entrambi i membri dell’equazione e sfruttando la regola della derivata della composizione, si ottiene \[ 1=\left(\log(e^x)\right)'=\frac{1}{e^x}(e^x)', \] da cui \[ (e^x)'=e^x,\; x \in \mathbb{R}. \]

Example 4.13 Si calcoli la derivata della funzione \(f:\mathbb{R} \to \mathbb{R}\), \[f(x)=e^{x^2}, \quad\text{ nel punto } \quad x=1.\] Sfruttando la regola di derivazione della composizione, si ha che \[f'(x)= e^{x^2} (x^2)'=e^{x^2}2x=2x\,e^{x^2},\] da cui \(f'(1)=2e\).

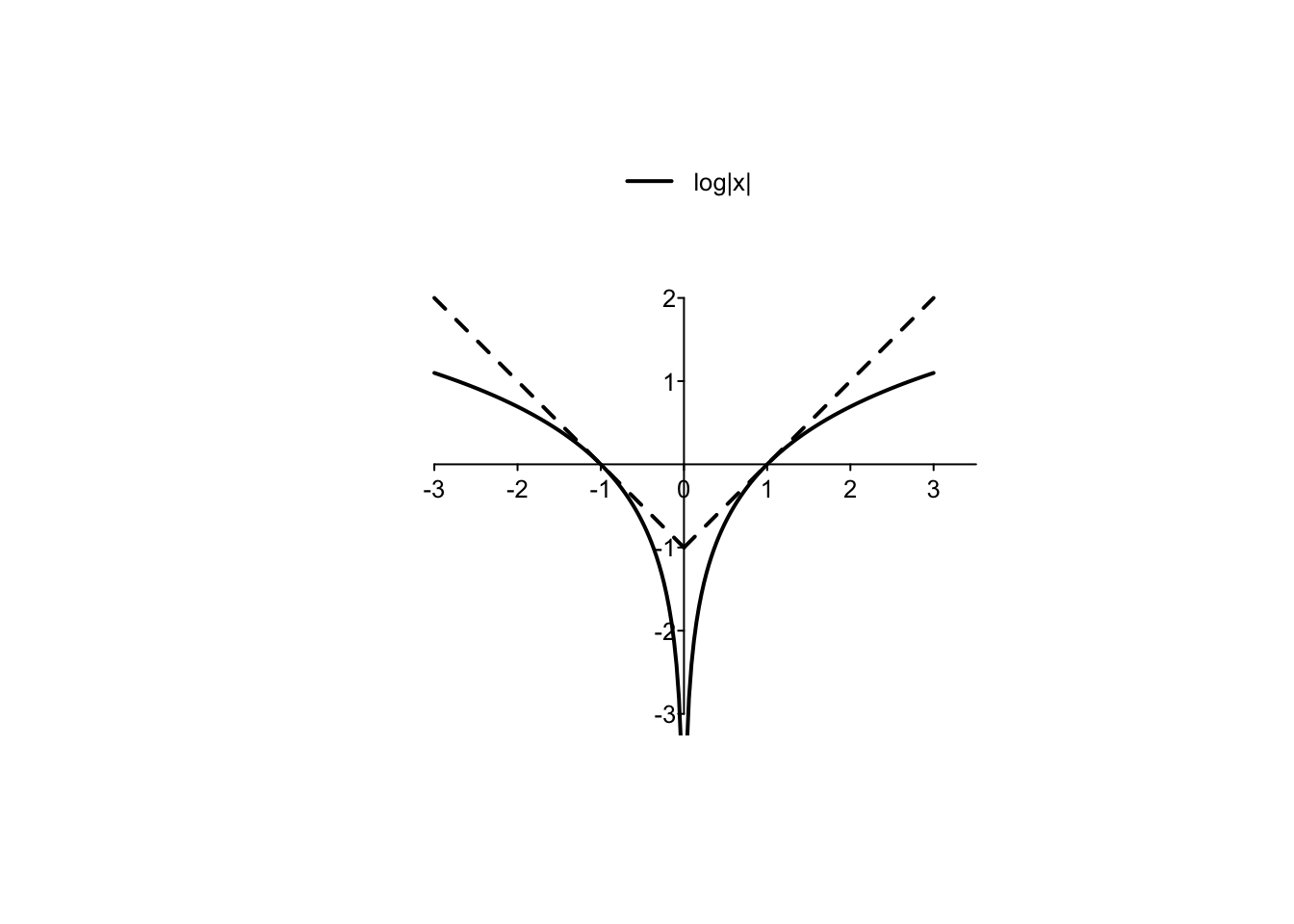
Example 4.14 Si calcoli la derivata della funzione \(f:\mathbb{R}\setminus \{0\} \to \mathbb{R}\), \[f(x)=\log |x|.\] Per valori di \(x\) positivi, si è già dimostrato che \((\log(x))'=\frac{1}{x}, \, x >0\). Per valori negativi, usando la regola di derivazione della composizione, si ottiene: \[ (\log(-x))'=\frac{1}{-x}(-x)'=-\left(\frac{1}{-x}\right)=\frac1x, \, x <0. \] Si ottiene quindi \(f'(x)=\frac{1}{x}\), per tutti gli \(x \neq 0\). Porre l’argomento del logaritmo all’interno di un valore assoluto permette di ampliarne il dominio naturale creando una funzione pari. Nella figura seguente si osservano i valori: \(f'(-1)=-1\), \(f'(1)=1\).

Conoscendo la derivata delle funzioni elementari (potenze, logaritmo ed esponenziale) e attraverso le regole di derivazione è possibile calcolare (meccanicamente) la derivata di qualsiasi funzione ottenuta tramite somma, prodotto, quoziente e composizione di funzioni elementari. Come visto negli esempi precedenti, nel calcolare la derivata è necessario prestare attenzione alla presenza:

di una radice, che tipicamente non è derivabile in un intorno (sinistro e/o destro) del punto in cui si annulla (in cui la derivata risulta infinita);
di un valore assoluto, che tipicamente crea un punto angoloso.

È possibile calcolare la derivata della composizione di più di due funzioni semplicemente applicando la corrispondente regola di derivazione più volte.

Example 4.15 Si trovi il dominio naturale \(D_f\), e nel caso sia derivabile si calcoli la derivata della funzione \(f:D_f \to \mathbb{R}\), \[ f(x)=\log^2(-x). \] Prima di tutto, si osservi che \(\log^2(-x)=[\log(-x)]^2\). Il dominio naturale della funzione è ristretto rispetto alla retta reale dalla presenza del logaritmo. Si deve richiedere che \(-x >0\), ovvero si ottiene \(D_f=(-\infty,0)\). Nel suo dominio naturale, la \(f\) è derivabile in quanto composizione di funzioni derivabili: \[ x \to -x\to\log(-x)\to[\log(-x)]^2. \] La derivata si calcola applicando la regola della derivata della composizione più volte: \[\begin{align*} \left([\log(-x)]^2\right)'&=2[\log(-x)]\cdot (\log(-x))' \\&=2[\log(-x)]\cdot \frac{1}{-x} \cdot(-x)'=2[\log(-x)]\cdot \frac{1}{-x} \cdot (-1)=\frac{2\log(-x)}{x}. \end{align*}\]

Analogamente, è possibile calcolare la derivata del prodotto di più di due funzioni derivabili semplicemente applicando la regola di derivazione del prodotto più volte.

4.5 Derivata e monotonia

Il calcolo della derivata di una funzione, quando possibile, permette di avere informazioni sulla sua monotonia: una funzione derivabile è crescente su un intervallo se e solo se possiede derivata non negativa.

Theorem 4.9 Sia \(f\) una funzione derivabile sull’intervallo \((a,b)\). La funzione è crescente in \((a,b)\) se e solo se possiede derivata non negativa \(f'(x) \geq 0\) per ogni \(x \in (a,b)\).

Proof. Dimostreremo solo il fatto che una funzione crescente ha derivata non negativa. Se \(f\) è crescente su \((a,b)\), significa che, per ogni \(x_1,x_2 \in (a,b)\), si ha che \[ x_1<x_2 \Rightarrow f(x_1) \leq f(x_2) \quad \text{e} \quad x_1>x_2 \Rightarrow f(x_1) \geq f(x_2), \] ovvero che \[ x_2-x_1 >0 \Rightarrow f(x_2)-f(x_1) \geq 0 \quad \text{e} \quad x_2-x_1 <0 \Rightarrow f(x_2)-f(x_1) \leq 0. \] In conclusione, per \(x_2 \neq x_1\), si ha che \[ \frac{f(x_2)-f(x_1)}{x_2-x_1} \geq 0. \] Ponendo \(x_2=x+h\) e \(x_1=x\) si ottiene che \[ \frac{f(x+h)-f(x)}{h} \geq 0, \quad h \neq 0. \] Essendo la funzione derivabile si può passare al limite e ricordando che il limite di una funzione non negativa deve essere non negativo, si ottiene che \[ f'(x)= \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \geq 0. \] Per dimostrare il viceversa, è necessaria l’applicazione del Teorema del Valor Medio che esula dagli scopi di questo testo.

Applicando il teorema a \(-f\), si ottiene che una funzione \(f\) è decrescente in \((a,b)\) se e solo se possiede derivata non positiva \(f'(x) \leq 0\) per ogni \(x \in (a,b)\).

È di grande utilità calcolare per quali punti una funzione derivabile possiede derivata non negativa per sapere su quali sottoinsiemi della retta reale essa è crescente/decrescente. Una volta calcolata la derivata della funzione, lo studio del suo segno procede mediante la risoluzione di una disequazione simile a quelle proposte alla fine del Capitolo 1.

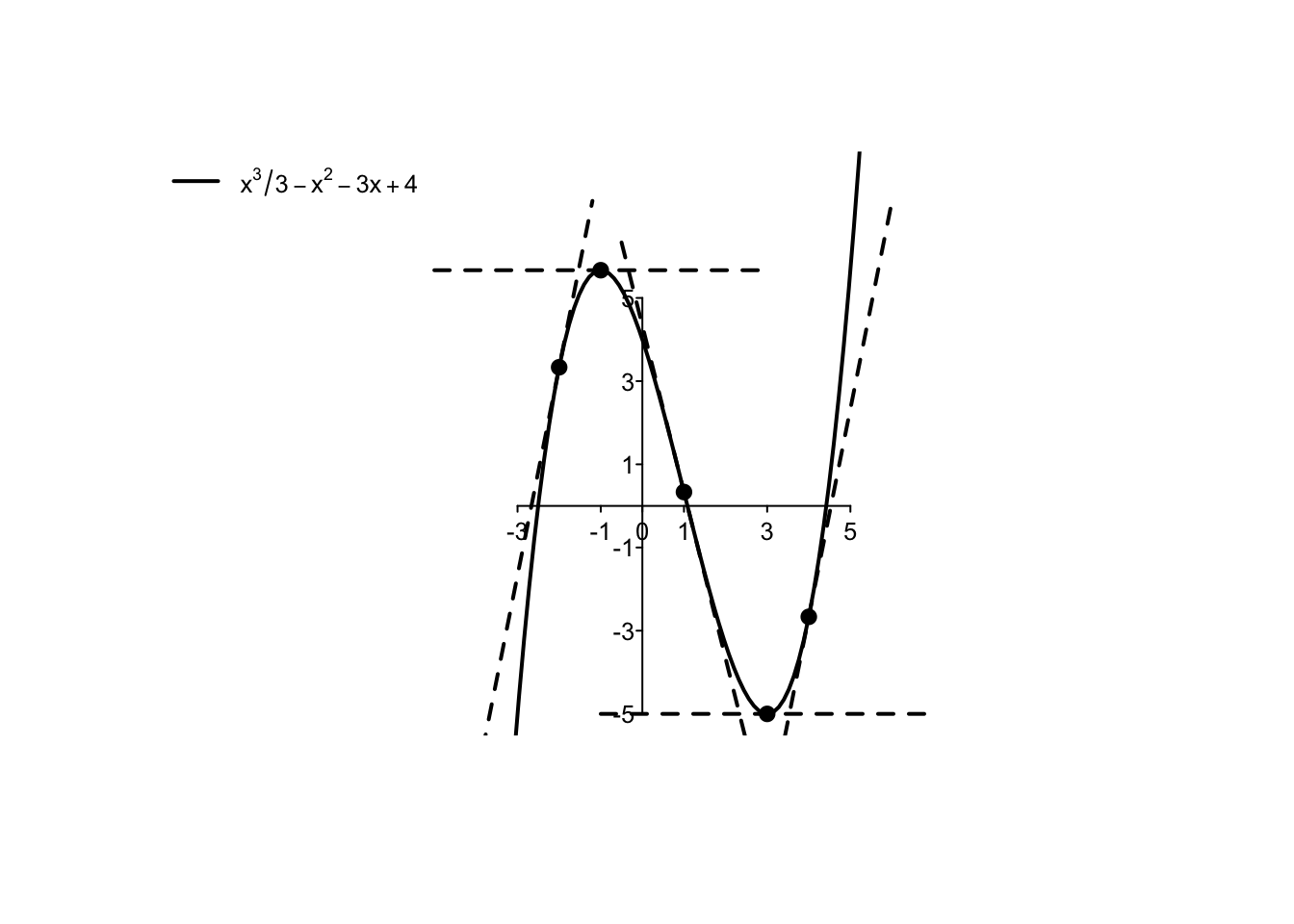
Example 4.16 Data la funzione \(f:\mathbb{R} \to \mathbb{R}\), \[ f(x)=\frac{x^{3}}{3}-x^{2}-3x+4, \] si calcoli la derivata prima \(f'(x)\) e per quale insieme di punti si ha \(f'(x)\geq 0\).

Usando la regola di derivazione di una potenza, si ottiene facilmente che \[ f'(x)=x^2-2x-3. \] Si procede quindi studiando la disequazione di secondo grado \[ x^2-2x-3 \geq 0, \] da cui si ricava che \(f'(x) \geq 0\) per \[ x \in (-\infty,-1]\cup \left[3,+\infty\right). \] La proprietà espressa dal Teorema precedente è immediatamente verificabile sul grafico della funzione. I punti \(x=-1\) e \(x=3\), dove la funzione passa prima da crescente a decrescente, poi da decrescente a crescente, saranno descritti come punti di massimo, rispettivamente, minimo locale nel Capitolo 5.

4.6 Derivata seconda e convessità

Dato che la derivata di una funzione è a sua volta una funzione, è naturalmente possibile calcolarne la derivata, ovvero calcolare la derivata di una derivata, che prende il nome di derivata seconda. La derivata seconda dà informazioni sulla convessità di una funzione.

Definition 4.2 La funzione derivabile \(f:A \subseteq \mathbb{R}\to \mathbb{R}\) si dice due volte derivabile nel punto interno \(x \in A\) se esiste finito \[ f''(x)=\lim_{h \to 0 } \,\frac{f'(x+h)-f'(x)}{h}. \] In tal caso, questo limite è detto derivata seconda della funzione \(f\) nel punto \(x\).

Se \(f\) è due volte derivabile per ogni \(x \in A\), con \(A\) aperto, si dice che \(f\) è due volte derivabile su \(A\) e si definisce la funzione derivata seconda \(f'':A \subseteq \mathbb{R} \to \mathbb{R},\, x \to f''(x)\), che associa ad ogni punto la derivata seconda della funzione in quel punto.

Remark. Osserviamo i seguenti punti fondamentali sulla definizione di derivata seconda:

secondo la definizione, la derivata seconda altro non è che il limite del rapporto incrementale della derivata, ovvero la derivata della derivata;
attraverso le regole di calcolo date in precedenza è possibile calcolare la derivata seconda di qualsiasi funzione ottenuta a partire dalle funzioni elementari introdotte tramite somma, prodotto, quoziente o composizione;
è analogamente possibile definire la derivata \(n-\)ma di una funzione che lo permetta. In questo caso, la funzione si dirà \(n\) volte derivabile.

Example 4.17 Si calcoli la derivata seconda della funzione \(f:\mathbb{R} \to \mathbb{R},\) \[ f(x)= x^2e^x. \] Attraverso la regola della derivata del prodotto, si calcola \[ f'(x)= (x^2)'e^x+x^2(e^x)'=2x\,e^x +x^2\,e^x=e^x(x^2+2x). \] Derivando una seconda volta, si ottiene infine \[ f''(x)= (e^x)'(x^2+2x)+ e^x(x^2+2x)'=e^x(x^2+2x)+ e^x(2x+2)=e^x(x^2+4x+2). \]

Si osservi che la derivata del prodotto di un polinomio per una esponenziale è sempre un polinomio (differente) per la stessa esponenziale (che può quindi essere sempre messa in evidenza).

Il calcolo della derivata seconda di una funzione, quando possibile, permette di avere informazioni sulla sua convessità. Si riprenda a tal proposito il grafico della funzione dell’Esempio 4.16. Si osserva che quando la funzione è concava la sua derivata è decrescente (passa da essere positiva, quindi nulla, infine negativa); quando è convessa, la sua derivata è cre-scente (passa da essere negativa, quindi nulla, infine positiva). Essendo la funzione un polinomio, quindi due volte (\(n\) volte) derivabile, applicando il Teorema 4.9, si deduce che la funzione è convessa quando la derivata della derivata è non negativa; è concava quando la derivata della derivata è non positiva.

Theorem 4.10 Sia \(f\) una funzione due volte derivabile sull’intervallo \((a,b)\). La funzione è convessa in \((a,b)\) se e solo se possiede derivata seconda non negativa \(f''(x) \geq 0\) per ogni \(x \in (a,b)\). La funzione è concava in \((a,b)\) se e solo se possiede derivata seconda non positiva \(f''(x) \leq 0\) per ogni \(x \in (a,b)\).

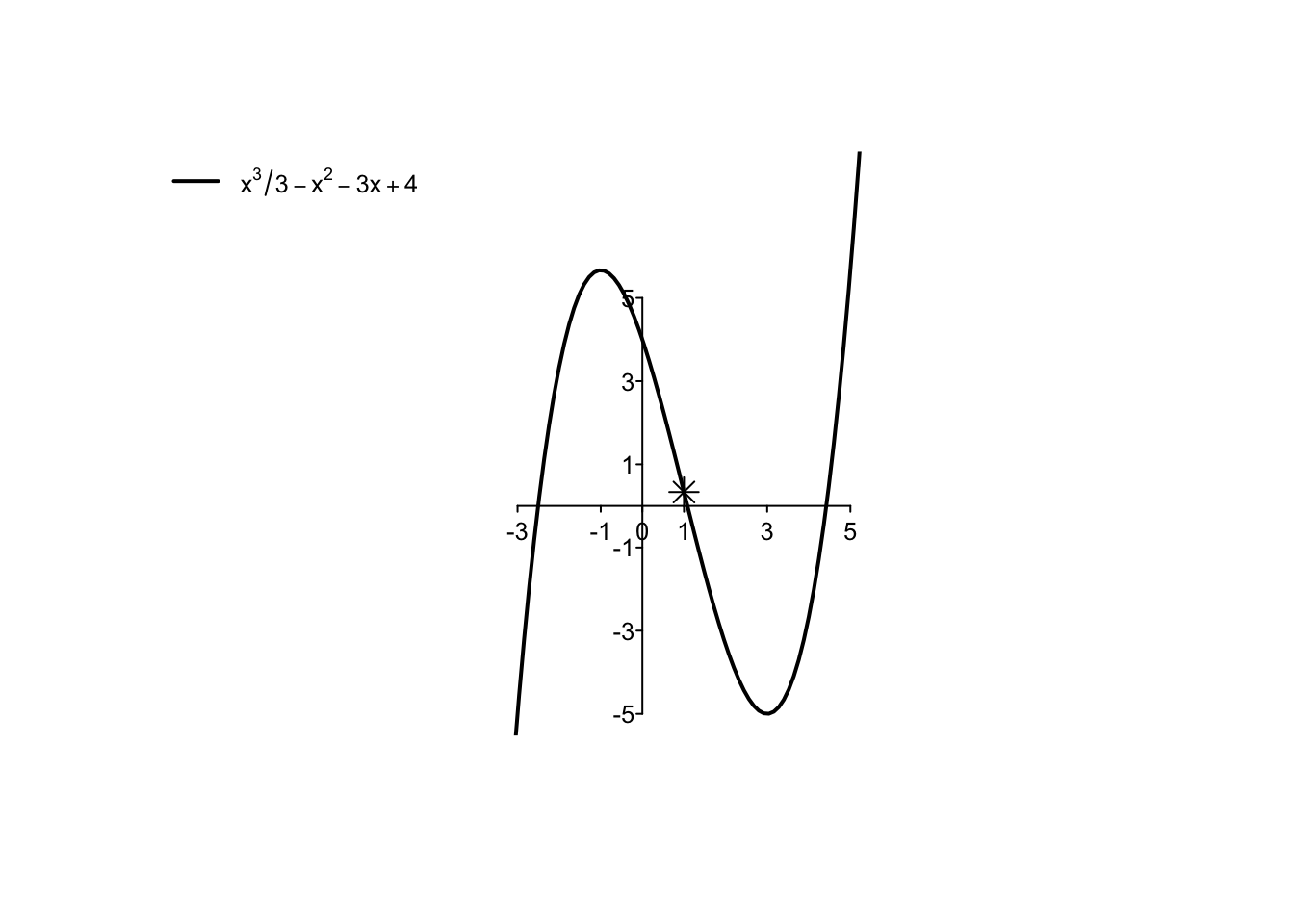
Example 4.18 Continuando l’Esempio 4.16, con \(f(x)=x^3/3-x^2-3x+4\) e \(f'(x)=x^2-2x-3\), si calcola \[ f''(x)=2x-2. \] Si ottiene quindi che la funzione è convessa per \(f''(x)=2x-2\geq 0\), ovvero per \(x \geq 1\). Il punto \(x=1\), dove la funzione passa da concava a convessa, sarà chiamato un punto di flesso nel Capitolo 5.

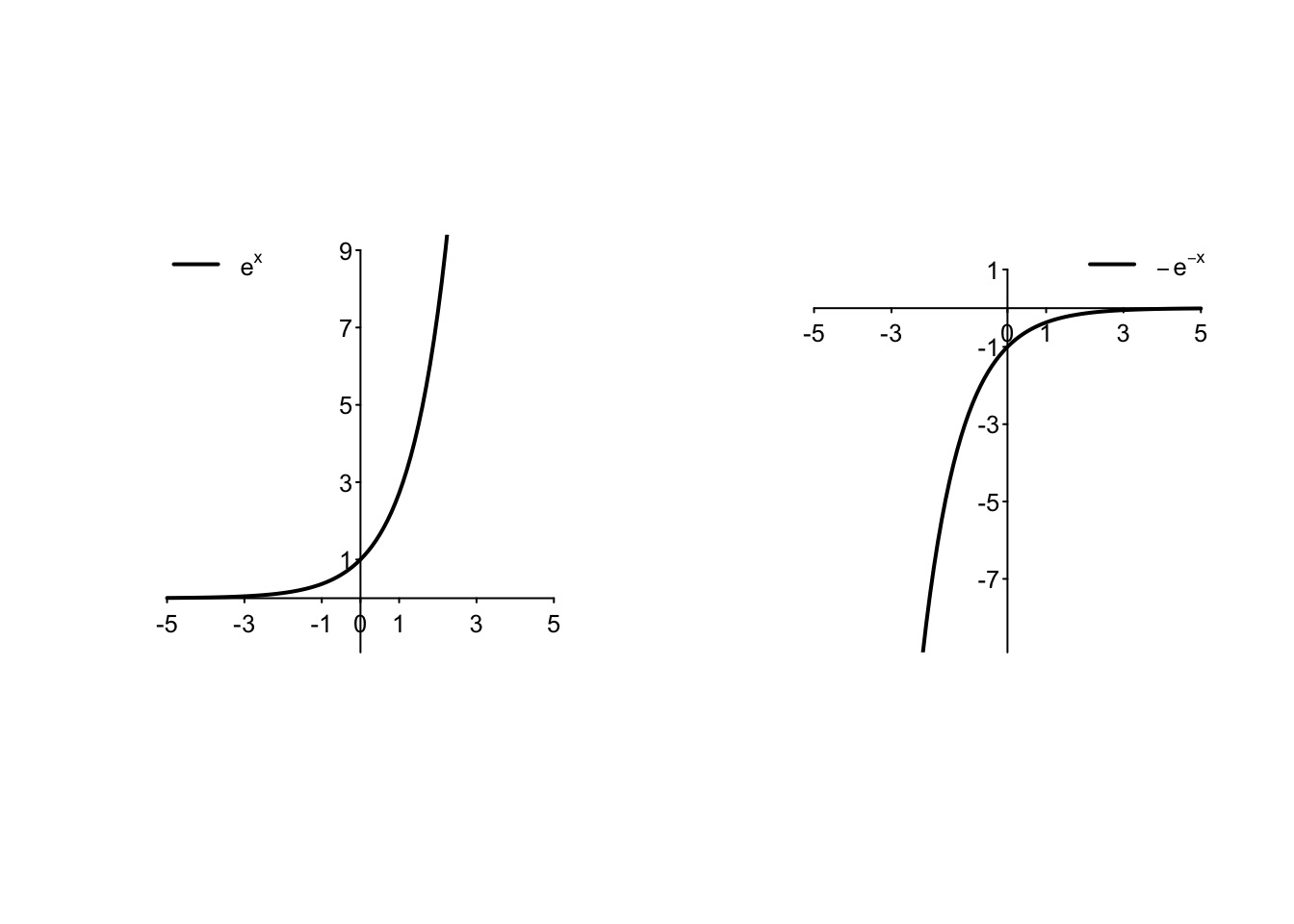
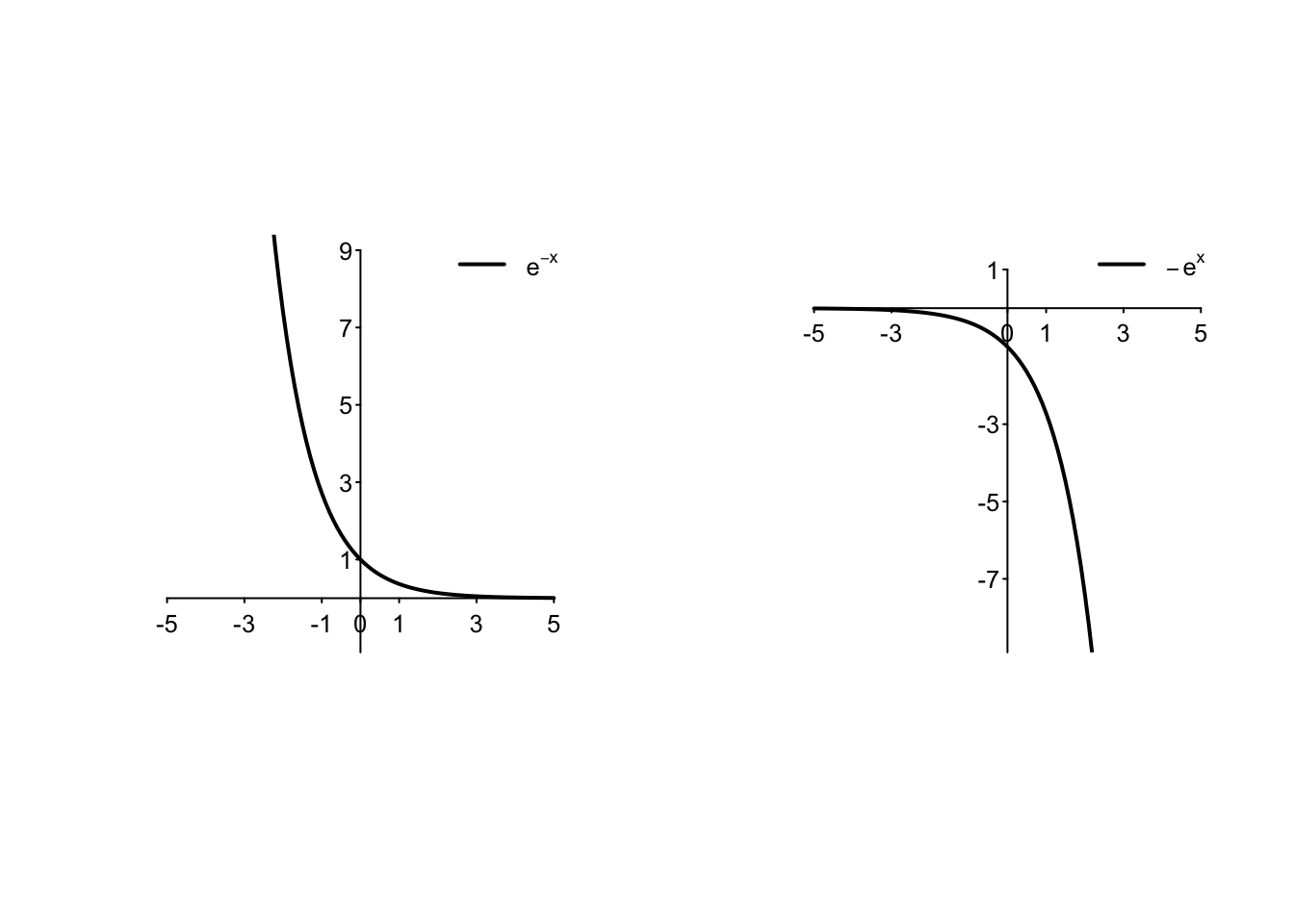
Le proprietà di monotonia (riconducibile per le funzioni derivabili al segno della derivata prima) e convessità (riconducibile per le funzioni due volte derivabili al segno della derivata seconda) sono indipendenti. Nella figura seguente vengono illustrate le quattro possibili variazioni di segno su una funzione esponenziale che definiscono: una funzione crescente e convessa; crescente e concava; decrescente e convessa; decrescente e concava.

4.7 Limiti tramite de l’Hôpital (D)

Il saper calcolare la derivata di una funzione ci fornisce un potente strumento per risolvere alcune forme indeterminate di limite che potrebbero non essere trattabili attraverso le casistiche esposte nel Capitolo 3. Consideriamo quindi una nuova casistica di limiti (D) da calcolare tramite i Teoremi di de l’Hôpital. Questi teoremi sono applicabili a forme indeterminate del tipo \(\frac{0}{0}\) oppure \(\frac{\pm \infty}{\pm \infty}\) e sono basati sul fatto che la derivata di una funzione fornisce una prima approssimazione della funzione stessa nel punto in cui la si calcola.

Theorem 4.11 (de l'Hôpital, 1) Siano \(f,g\) due funzioni continue su \([a,b]\) e derivabili su \((a,b)\setminus \{x_0\}\), \(x_0 \in (a,b)\), tali che \(f(x_0)=g(x_0)=0\). Se \(g(x), g'(x) \neq 0\) per ogni \(x \in (a,b)\setminus \{x_0\}\) ed esiste (finito o infinito) il limite \[ \lim_{x \to x_0} \frac{f'(x)}{g'(x)}=L \in\mathbb{R}^*, \] allora esiste anche il limite \[ \lim_{x \to x_0} \frac{f(x)}{g(x)}=\lim_{x \to x_0} \frac{f'(x)}{g'(x)}=L \in\mathbb{R}^*. \]

Proof. Per semplicità, proveremo il risultato nel caso in cui \(f\) e \(g\) siano derivabili in \(x=x_0\) con derivate \(f',g'\) continue. In questo caso si ha \[ \lim_{x \to x_0} \frac{f(x)}{g(x)}=\lim_{x \to x_0}\, \frac{\frac{f(x)-0}{x-x_0}}{\frac{g(x)-0}{x-x_0}}=\lim_{x \to x_0}\,\frac{\frac{f(x)-f(x_0)}{x-x_0}}{\frac{g(x)-g(x_0)}{x-x_0}}= \frac{f'(x_0)}{g'(x_0)}=\lim_{x \to x_0}\,\frac{f'(x)}{g'(x)}. \]

Theorem 4.12 (de l'Hôpital, 2) Siano \(f,g\) due funzioni derivabili su \((a,b)\setminus \{x_0\}\), \(x_0 \in (a,b)\), tali che \[ \lim_{x \to x_0} f(x)=\lim_{x \to x_0} g(x)=+\infty. \] Se \(g(x), g'(x) \neq 0\) per ogni \(x \in (a,b)\) ed esiste (finito o infinito) il limite \[ \lim_{x \to x_0} \frac{f'(x)}{g'(x)}=L \in\mathbb{R}^*. \] Allora, esiste anche il limite \[ \lim_{x \to x_0} \frac{f(x)}{g(x)}=\lim_{x \to x_0} \frac{f'(x)}{g'(x)}=L \in\mathbb{R}^*. \]

Remark. Osserviamo i seguenti punti fondamentali sui Teoremi de l’Hôpital:

i teoremi si applicano esclusivamente alle forme indeterminate \(\frac{0}{0}\) e \(\frac{\pm \infty}{\pm \infty}\), utilizzando in quest’ultimo caso la formulazione del secondo teorema a meno di un cambiamento di segno del numeratore e/o del denominatore. I teoremi nulla predicono nel caso di altre forme indeterminate;
i teoremi valgono analogamente anche nei casi in cui si abbia \(x_0=+\infty\) o \(x_0=-\infty\);
i teoremi calcolano il limite del rapporto di due funzioni come il limite (se esiste) del rapporto delle loro derivate. Quindi non si deve calcolare la derivata del rapporto, ma singolarmente le derivate del numeratore e del denominatore;
se non esiste il limite del rapporto delle derivate, i teoremi non predicono il limite del rapporto delle funzioni;
se esiste il limite del rapporto delle funzioni, non è detto che esista il limite del rapporto delle loro derivate;
se possibile, è sempre consigliabile trattare un limite con le casistiche studiate in precedenza. I Teoremi di de l’Hôpital sono molto potenti, ma proprio per questo va controllata accuratamente la validità delle loro ipotesi e l’eventuale complessità del calcolo delle derivate;
i teoremi sono applicabili anche più volte, come nel seguente esempio.

Example 4.19 Si calcoli \[ \lim_{x \to 0}\, \frac{e^x-1-x}{x^2}. \]

Siamo in presenza di una forma indeterminata \(\frac{0}{0}\) che rispetta le ipotesi del corrispondente Teorema di de l’Hôpital, attraverso cui si ottiene \[ \lim_{x \to 0}\, \frac{e^x-1-x}{x^2}=\lim_{x \to 0}\, \frac{e^x-1}{2x}, \] sotto condizione che questo ultimo limite esista. Trattandosi ancora di una forma indeterminata \(\frac{0}{0}\), è possibile iterare il procedimento ottenendo \[ \lim_{x \to 0}\, \frac{e^x-1-x}{x^2}=\lim_{x \to 0}\, \frac{e^x-1}{2x}=\lim_{x \to 0}\, \frac{e^x}{2}=\frac{1}{2}. \] È importante osservare che le uguaglianze precedenti debbono essere scritte “a ritroso”, ovvero valgono solo se vale l’ultima (ovvero se il limite del rapporto tra le derivate esiste). Dai calcoli precedenti segue anche il limite notevole \[ \boldsymbol{\lim_{x \to 0}\, \frac{e^x-1}{x}=1}. \]

Attraverso i Teoremi di de l’Hôpital si può verificare il Teorema 3.6 sulla Gerarchia degli Infiniti delle funzioni elementari.

Example 4.20 Si calcoli \[ \lim_{x \to +\infty}\, \frac{\log (x)}{x^q}= 0, \quad q \in \mathbb{Q},\, q>0. \] Siamo in presenza di una forma indeterminata \(\frac{+\infty}{+\infty}\). Si ottiene \[ \lim_{x \to +\infty}\, \frac{\log (x)}{x^q}=\lim_{x \to +\infty}\, \frac{x^{-1}}{q\,x^{q-1}}=\lim_{x \to +\infty}\,\frac{1}{q\,x^q}=0. \]

Example 4.21 Si calcoli \[ \lim_{x \to +\infty} \,\frac{e^x}{x^q}= +\infty, \quad q \in \mathbb{Q},\, q>0. \] Scrivendo il limite come \[ \lim_{x \to +\infty} \,\left(\frac{e^{\frac{x}{q}}}{x}\right)^q, \] e applicando il Teorema di de l’Hôpital alla forma indeterminata \(\frac{+\infty}{+\infty}\) che è all’argomento della potenza si ottiene \[ \lim_{x \to +\infty} \,\frac{e^{\frac{x}{q}}}{x}=\lim_{x \to +\infty} \,\frac{e^{\frac{x}{q}}}{q}=+\infty, \] da cui per continuità della funzione potenza si ottiene \[ \lim_{x \to +\infty} \,\frac{e^x}{x^q}=\lim_{x \to +\infty} \,\left(\frac{e^{\frac{x}{q}}}{x}\right)^q= (+\infty)^q=+\infty. \]

Questo capitolo si chiude con alcuni esempi di forme indeterminate non trattabili tramite le casistiche studiate nel capitolo 3, e che possono essere risolte tramite i Teoremi di de l’Hôpital.

Example 4.22 Si calcoli \[ \lim_{x \to 0^+} x \log (x). \] In questo caso si ha una forma indeterminata del tipo \(0\cdot(-\infty)\). I Teoremi di de l’Hôpital possono essere applicati anche in questo caso, scrivendo \[ \lim_{x \to 0^+} x \log (x) = \lim_{x \to 0^+} \, \frac{\log (x)}{x^{-1}}, \] che è una forma indeterminata del tipo \(\frac{+\infty}{+\infty}\). Si ha quindi \[ \lim_{x \to 0^+} x \log (x) = \lim_{x \to 0^+} \, \frac{\log (x)}{x^{-1}}= \lim_{x \to 0^+} \, \frac{x^{-1}}{-x^{-2}}=\lim_{x \to 0^+} -x=0. \]

Nell’applicazione dei Teoremi di de l’Hôpital alle forme \(0\cdot(\pm \infty)\) come nell’esempio precedente, si osservi che fa differenza quale funzione si scrive al numeratore, e quale (opposta) al denominatore. Nell’esempio precedente ottenere una forma indeterminata \(\frac{0}{0}\) del tipo \[ \lim_{x \to 0^+} x \log (x) = \lim_{x \to 0^+} \, \frac{x}{(\log (x))^{-1}} \] non avrebbe condotto a facile risoluzione.

Example 4.23 Si dimostri il limite notevole \[ \boldsymbol{\lim_{x \to 0}\, \frac{\log(x+1)}{x}=1}. \]

Applicando il Teorema di de l’Hôpital alla forma \(\frac{0}{0}\), si ottiene: \[ \lim_{x \to 0}\, \frac{\log(x+1)}{x}=\lim_{x \to 0}\, \frac{(x+1)^{-1}}{1}= \lim_{x \to 0}\, \frac{1}{x+1}=1. \]

Example 4.24 Si dimostri il limite notevole \[\begin{equation} \boldsymbol{\lim_{x \to +\infty} \left(1 +\frac1x \right)^x=e}. \tag{4.1} \end{equation}\]

Nei casi in cui la variabile \(x\) compare anche all’esponente, è consigliabile scrivere il limite come \[ \lim_{x \to +\infty} \left(1 +\frac1x \right)^x = \lim_{x \to +\infty} e^{ \log\left(1 +\frac1x \right)^x}=\lim_{x \to +\infty} e^{ x\,\log\left(1 +\frac1x \right)}. \] A questo punto, si risolve \[\begin{align*} \lim_{x \to +\infty} x\,\log\left(1 +\frac1x \right)= &\lim_{x \to +\infty}\, \frac{\log\left(1 +\frac1x \right)}{x^{-1}} \\= &\lim_{x \to +\infty} \frac{\left(1 +\frac1x \right)^{-1}\left(-\frac{1}{x^2}\right)}{\left(-\frac{1}{x^2}\right)} =\lim_{x \to +\infty}\, \left(1 +\frac1x \right)^{-1}=1, \end{align*}\] da cui, per continuità della funzione esponenziale, si arriva infine a \[ \lim_{x \to +\infty} \left(1 +\frac1x \right)^x = \lim_{x \to +\infty} e^{ \log\left(1 +\frac1x \right)^x}=\lim_{x \to +\infty} e^{ x\,\log\left(1 +\frac1x \right)}=e^{1}=e. \]

Ci sono altre casistiche di limite (molto) più complesse di quelle trattate in questo testo, ma esse esulano dagli scopi di questo corso.

4.8 Esercizi

Ai fini dello studio di una funzione reale (descritto nel Capitolo 5) e per capire dove una funzione presenta massimi e minimi, è fondamentale studiare il segno delle sue derivate.

Per le funzioni \(f(x)\) indicate, si calcoli: la derivata prima \(f'(x)\) e per quale insieme di punti \(x\) si ha \(f'(x)\geq 0\); la derivata seconda \(f''(x)\) e per quale insieme di punti \(x\) si ha \(f''(x)\geq 0\).

Exercise 4.1

\(f(x)= \frac{2x^2}{3-x}\)

Exercise 4.2

\(f(x)= \sqrt{x^2-2x}-x\)

Exercise 4.3

\(f(x)= \log \left( \frac{2-x}{x-4} \right)\)

Exercise 4.4

\(f(x)= x e^{-1/x}\)

Exercise 4.5

\(f(x)= \frac{x^2-4x+1}{x}\)

Exercise 4.6

\(f(x)= \frac{5x^2-2x}{e^x}\)

Exercise 4.7

\(f(x)= \frac{(x-3)^2}{(x-2)}\)

Exercise 4.8

\(f(x)= x + \sqrt{1-x}\)

Exercise 4.9

\(f(x)= \frac{\log(x^3)}{x^2}\)

Exercise 4.10

\(f(x)= \frac{-x^2-3x+3}{e^x}\)

Exercise 4.11

\(f(x)= \frac{e^{x-1}}{(x-2)^2}\)

Exercise 4.12

\(f(x)= e^{\frac{2x-1}{x}}\)

Exercise 4.13

\(f(x)= \frac{e^x+2}{e^x-3}\)

Exercise 4.14

\(f(x)= \frac{1-x}{1+x^2}\)

Exercise 4.15

\(f(x)= x-\sqrt{x^2-4}\)

Exercise 4.16

\(f(x)= \frac{e^{2x}}{x^3}\)

Exercise 4.17

\(f(x)= \frac{\sqrt{x}}{x+1}\)

Exercise 4.18

\(f(x)= \frac{2x^2-x-2}{x-1}\)

Exercise 4.19

\(f(x)= \log \left( \frac{1-x}{x-5} \right)\)

Exercise 4.20

\(f(x)= 3x - \sqrt{x^2-16}\)