3 Limiti e continuità

Il concetto di limite descrive il comportamento di una funzione nelle vicinanze di un determinato punto del sistema ampliato dei numeri reali. Non esiste un metodo generale e meccanico per calcolare qualsiasi limite, ed è sempre possibile creare un limite estremamente complesso o impossibile da risolvere. L’obiettivo di questo capitolo è quindi quello di fornire varie casistiche di modo che sia possibile riconoscere quale procedura di calcolo si adatti meglio al limite sotto studio. Per introdurre il concetto di limite, prendiamo in considerazione una ultima classe di funzioni.

3.1 Funzioni omografiche

Le funzioni reali del tipo $f: \mathbb{R}\setminus\left\{-\frac{d}{c}\right\} \to \mathbb{R},$ \[ f(x)=\frac{ax+b}{cx+d}, \quad a,b,c,d \in \mathbb{R},\quad c \neq 0, \quad ad \neq bc, \] sono dette funzioni omografiche. Essendo un rapporto tra due funzioni lineari, il punto $x=-\frac{d}{c}$ in cui si annulla il denominatore viene escluso dal loro dominio (naturale). I casi $c=0$ e $ad=bc$ non sono considerati dalla definizione perché corrispondono ad una funzione lineare (retta) già trattata nel Capitolo 2 (si provi a sostituire $c=0$ oppure $b=ad/c$ nell’equazione precedente).

Il grafico della funzione omografica è una iperbole equilatera. È semplice disegnare tale grafico se si analizzano i valori che la funzione assume vicino ai punti di frontiera del suo dominio naturale:

quando $x$ diviene arbitrariamente grande (o arbitrariamente piccola) le due costanti presenti al numeratore e al denominatore diventano trascurabili rispetto ai coefficienti della $x$, quindi la funzione si avvicina al loro rapporto: \[ \frac{ax+b}{cx+d} \to \frac{a}{c}; \]
quando $x$ si avvicina al valore $-\frac{d}{c}$, il denominatore si avvicina a zero e la funzione tende ad assumere valori arbitrariamente grandi o arbitrariamente piccoli a seconda del suo segno (arbitrariamente grandi in valore assoluto): \[ \left| \frac{ax+b}{cx+d} \right | \to +\infty. \]

Queste osservazioni possono essere verificate nell’esempio seguente.

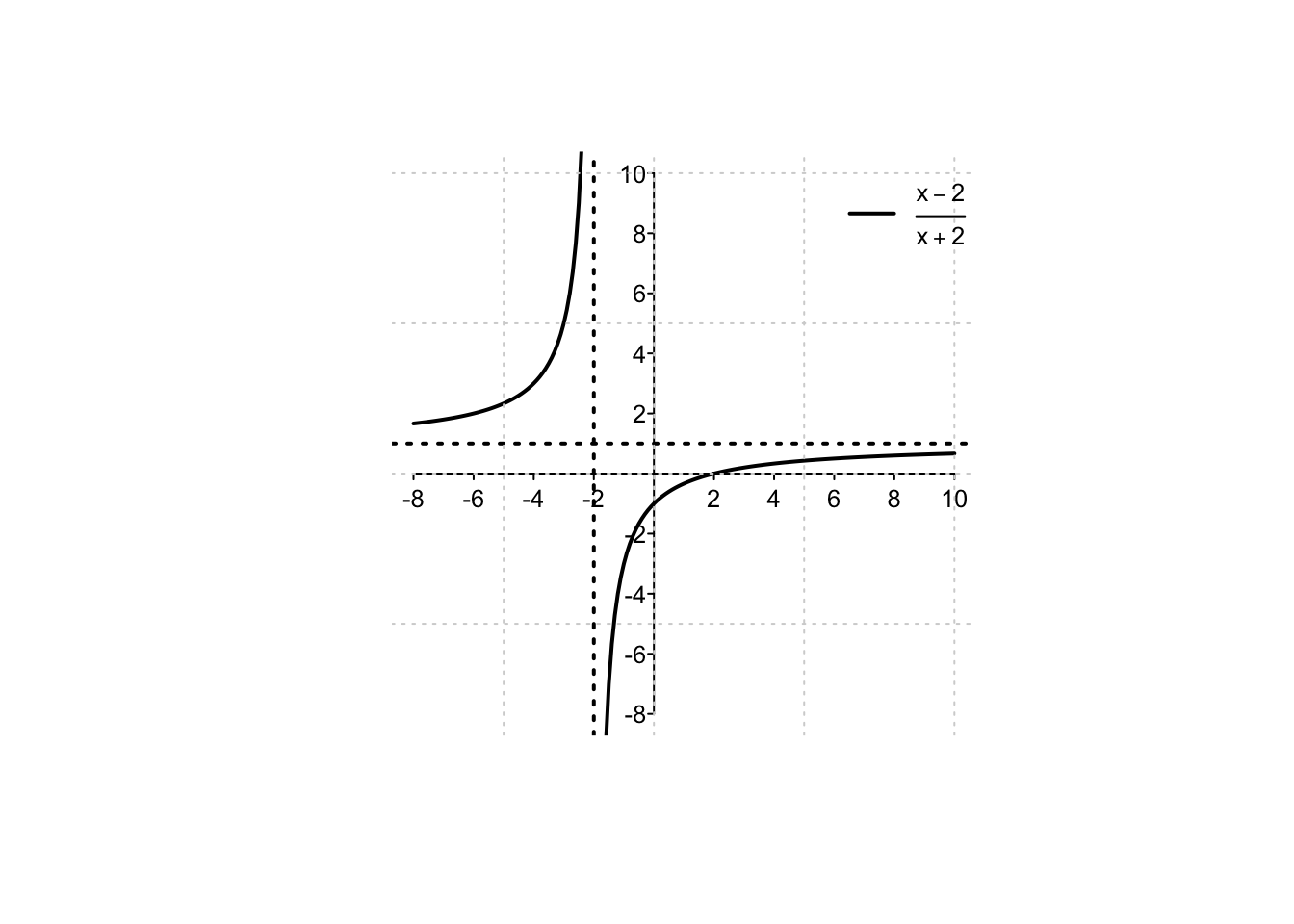
Example 3.1 Ricordando il comportamento di una funzione omografica, si tracci il grafico della funzione \[f(x)=\frac{x-2}{x+2}.\]

3.2 Definizione di limite

Concetti come il “diventare arbitrariamente grande/piccola” o l’“avvicinarsi ad un punto”, intuitivamente chiari, possono essere facilmente formalizzati con la nozione già introdotta di intorno. Grazie a questa possiamo dare la seguente definizione di limite.

Definition 3.1 Siano dati la funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$, e $x_0 \in \mathbb{R^*}$ punto di accumulazione per $A$. Si dice che il limite di $f$ per $x$ che tende a $x_0$ è uguale ad $L\in \mathbb{R^*}$ e si scrive \[ \lim_{x \to x_0} f(x) =L, \] se per qualsiasi intorno $I(L)$ di $L$, è possibile trovare un intorno $I(x_0)$ di $x_0$ tale che: \[\begin{equation} \text{ per ogni } x \in A \cap I(x_0)\setminus\{x_0\}, \text{ si ha che } f(x) \in I(L). \tag{3.1} \end{equation}\]

Remark. Osserviamo i seguenti punti fondamentali sulla definizione di limite:

la definizione traduce matematicamente, attraverso il concetto di intorno, il fatto che quando la variabile $x$ è vicina a $x_0$, allora la sua immagine $f(x)$ è vicina a $L$;
la (3.1) può essere scritta più elegantemente come $f(A \cap I(x_0)\setminus\{x_0\}) \subseteq I(L)$;
il valore di un limite non dipende da quello che accade nel punto in cui lo si calcola, che è esplicitamente escluso dalla definizione. Si osservi che non è nemmeno necessario che $x_0$ appartenga al dominio della funzione (sarà necessario effettuare il calcolo dei limiti proprio nei punti di frontiera del suo dominio naturale, dove la funzione non è definita);
il valore di un limite non comunica il comportamento della funzione nel punto $x_0$ in cui lo si calcola, ma vicino al punto $x_0$;
per far sì che l’intorno $I(x_0)$ nella definizione non sia vuoto è necessario richiedere che il punto $x_0$ sia un punto di accumulazione per il dominio della funzione (ciò non implica che il punto $x_0$ appartenga al dominio, ma che in ogni suo intorno si possa trovare un punto del dominio distinto da $x_0$);
la definizione data corrisponde a quella probabilmente studiata nella scuola secondaria. La richiesta $f(x) \in I(L)$ equivale ad una disequazione del tipo $\vert f(x)-L\vert < \epsilon$, mentre il fatto che essa debba valere$\text{ per ogni } x \in A \cap I(x_0)\setminus\{x_0\}$ equivale ad una disequazione del tipo $0<\vert x-x_0\vert < \delta$. Si può verificare allora che nel caso $x_0,L \in \mathbb{R}$, si ottiene la classica definizione “epsilon-delta” per cui $\lim_{x \to x_0} f(x) =L$ se \[ \forall\, \epsilon>0 \quad \exists\, \delta>0 \quad \text{tale che}\quad 0<\vert x-x_0\vert < \delta \;\Rightarrow\; \vert f(x)-L\vert < \epsilon; \]
la definizione vale (e analogamente potrebbe essere riscritta in forma estesa) anche quando $x_0,L=\pm \infty$;
nel seguito, leggeremo la notazione $x \to x_0$ come “$x$ tende a $x_0$”.

Quando nella definizione si utilizza solo l’intorno sinistro o destro del punto in cui si calcola il limite, si parla di limite sinistro o destro.

Definition 3.2 Siano dati la funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$, e $x_0 \in \mathbb{R}$ punto di accumulazione per $A^-=A \cap (-\infty,x_0]$. Si dice che il limite sinistro di $f$ per $x$ che tende a $x_0$ è uguale ad $L\in \mathbb{R^*}$ e si scrive \[ \lim_{x \to x_0^-} f(x) =L, \] se per qualsiasi intorno $I(L)$ di $L$, è possibile trovare un intorno sinistro $I^-(x_0)$ di $x_0$ tale che: \[ f(A \cap I^-(x_0)) \subseteq I(L). \]

Definition 3.3 Siano dati la funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$, e $x_0 \in \mathbb{R}$ punto di accumulazione per $A^+=A \cap [x_0,+\infty)$. Si dice che il limite destro di $f$ per $x$ che tende a $x_0$ è uguale ad $L\in \mathbb{R^*}$ e si scrive \[ \lim_{x \to x_0^+} f(x) =L, \] se per qualsiasi intorno $I(L)$ di $L$, è possibile trovare un intorno destro $I^+(x_0)$ di $x_0$ tale che: \[ f(A \cap I^+(x_0)) \subseteq I(L). \]

Dalle definizioni date, e dal fatto (già messo in evidenza nel Capitolo 1) che \[ I^-(x_0) \cup I^+(x_0)= I(x_0) \setminus \{x_0\}, \] segue immediatamente che un limite esiste se e solo se esistono e sono uguali entrambi i rispettivi limiti sinistro e destro.

Theorem 3.1 Siano dati la funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$, e $x_0 \in \mathbb{R}$ punto di accumulazione sia per $A^-=A \cap (-\infty,x_0]$ che per $A^+=A \cap [x_0,+\infty)$. Allora \[ \lim_{x \to x_0} f(x) =L, \] se e solo se \[ \lim_{x \to x_0^-} f(x)=\lim_{x \to x_0^+} f(x) =L. \]

Come vedremo quando verrà trattato il concetto di continuità di una funzione, è naturalmente possibile che il limite di una funzione in un punto non esista. Ad esempio si potrebbe avere che i suoi limiti sinistro e destro non coincidano. Se invece il limite esiste, è facile dimostrare che esso è unico.

Theorem 3.2 (Unicità del Limite) Siano dati $f: A \subseteq \mathbb{R} \to \mathbb{R}$, e $x_0$ punto di accumulazione per $A$. Se $\lim_{x \to x_0} f(x)=L_1$ e $\lim_{x \to x_0} f(x)=L_2$, allora $L_1=L_2$.

Proof. Se $L_1 \neq L_2$ allora è possibile trovare due intorni $I(L_1)$ e $I(L_2)$ tali che $I(L_1) \cap I(L_2)=\emptyset$. Se $\lim_{x \to x_0} f(x)=L_1$, allora esiste $I(x_0)$ tale che \[ f(A \cap I(x_0) \setminus \{x_0\}) \subseteq I(L_1). \] Di conseguenza, dato che $x_0$ è di accumulazione per $A$, esiste $a \in I(x_0)\cap A, a \neq x_0$, tale che $f(a) \in I(L_1)$.

Se $\lim_{x \to x_0} f(x)=L_2$, allora esiste un altro intorno $I'(x_0)$ tale che \[ f(A \cap I'(x_0) \setminus \{x_0\}) \subseteq I(L_2). \]
Supponiamo che $I(x_0) \subseteq I'(x_0)$ (altrimenti si scambino $L_1$ e $L_2$). Allora il punto $a$ precedentemente trovato appartiene anche a $I'(x_0)$ e si ha anche $f(a) \in I(L_2)$.

Ma allora $f(a)$ appartiene sia a $I(L_1)$ che a $I(L_2)$ e questo è in contraddizione col fatto che $I(L_1) \cap I(L_2)=\emptyset$. La contraddizione è superata assumendo che $L_1=L_2$.

Useremo spesso nel seguito il fatto che, se il limite di una funzione è positivo, allora essa permane positiva in un intorno sufficientemente piccolo del punto. Il seguente è il cosiddetto Teorema della Permanenza del Segno.

Theorem 3.3 (Permanenza del Segno) Siano dati $f: A \subseteq \mathbb{R} \to \mathbb{R}$, e $x_0$ punto di accumulazione per $A$. Se $\lim_{x \to x_0} f(x)=L>0$, allora esiste un intorno $I(x_0)$ tale che \[ f(A \cap I(x_0) \setminus \{x_0\}) \subseteq (0, +\infty). \]

Proof. Il teorema segue immediatamente dalla definizione di limite prendendo l’intorno $I(L)=\left(\frac{L}{2},\frac{3}{2}L\right) \subseteq (0, +\infty)$, se $L \in \mathbb{R}$; l’intorno $(0,+\infty)$, se $L=+\infty$.

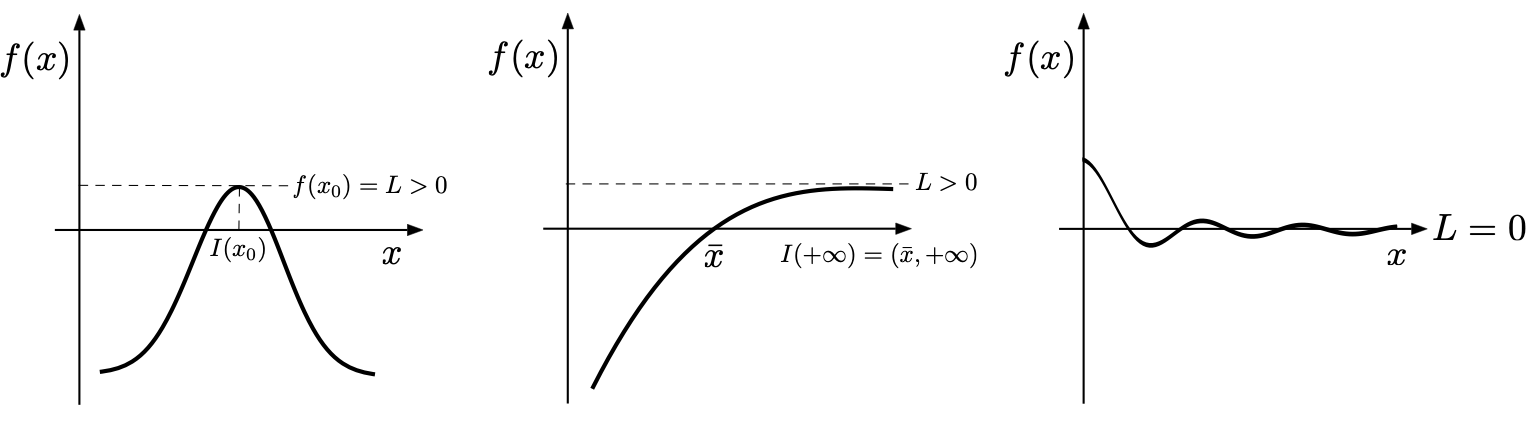
Nella figura seguente (a sinistra) viene illustrato il caso in cui $\lim_{x \to x_0} f(x)=f(x_0)>0$: la funzione permane positiva in un intorno del punto $x_0$. Al centro invece viene raffigurato il caso in cui $\lim_{x \to +\infty} f(x)=L>0$: la funzione permane positiva in un intorno di $+\infty$, ovvero per valori $x>\bar{x}$.

Il Teorema di Permanenza del Segno vale analogamente per le funzioni aventi limite $L<0$: esse permangono negative in un intorno del punto (la dimostrazione è analoga). Diverso il caso in cui il limite di una funzione sia nullo: la funzione potrebbe oscillare presentando sia valori positivi che negativi (figura seguente, a destra).

Si osservi che il Teorema di Permanenza del Segno implica anche che una funzione non negativa dovrà avere limite non negativo (se lo avesse negativo permarrebbe negativa almeno in un intorno del punto in oggetto).

A chiusura delle principali proprietà dei limiti, enunciamo il seguente teorema (di facile dimostrazione).

Theorem 3.4 Per due funzioni $f,g: A \subseteq \mathbb{R} \to \mathbb{R}$, e $x_0 \in \mathbb{R}^*$ punto di accumulazione per il loro (comune) dominio $A$, si assuma che esistano (finiti o infiniti) i limiti \[ \lim_{x \to x_0} f(x) =L \in \mathbb{R}^*, \quad \lim_{x \to x_0} g(x) =M \in \mathbb{R}^*. \] Allora, se le seguenti operazioni indicate a destra dei segni di eguaglianza sono eseguibili su $\mathbb{R}^*$ (cioè se non compaiono forme indeterminate), si ha che:

il limite della somma è la somma dei limiti: \[ \lim_{x \to x_0} f(x) + g(x) = L+M; \]
il limite del prodotto è il prodotto dei limiti: \[ \lim_{x \to x_0} f(x)g(x) = L\,M; \]
se $L\in \mathbb{R}^*$, e $M \in \mathbb{R} \setminus \{0\}$, il limite del quoziente è il quoziente dei limiti: \[ \lim_{x \to x_0} \frac{f(x)}{g(x)} = \frac{L}{M}; \]
se $g(x) \neq 0$ per $x \neq x_0$, $L\in \mathbb{R}^* \setminus \{0\}$ e $M=0$, si ha \[ \lim_{x \to x_0} \left|\frac{f(x)}{g(x)}\right| = + \infty; \]

Relativamente al quoziente $\frac{f(x)}{g(x)}$, non è necessario indicare che $g(x) \neq 0$ se $\lim_{x \to x_0} g(x) =M \neq 0$. Se la funzione tende ad un limite diverso da zero, in un intorno sufficientemente piccolo del punto essa permarrà dello stesso segno del suo limite, quindi non potrà annullarsi.

Si ricordi che non tutte le operazioni tra $L$ e $M$ sono possibili sul sistema ampliato dei numeri reali. Tra quelle studiate, rimangono indeterminate le forme \[+\infty+(-\infty), \,-\infty+(+\infty),\, 0\cdot(\pm\infty), \,(\pm \infty)\cdot 0,\, \frac{\pm \infty}{\pm \infty},\, \frac{0}{0}.\]

3.3 Asintoti orizzontali e verticali

Nell’Esempio 3.1, si verifica che \[ \lim_{x \to +\infty} \frac{x-2}{x+2}=1. \] In questo caso, si dice che il grafico della funzione ha un asintoto orizzontale.

Definition 3.4 Diremo che il grafico di una funzione $f$ per cui vale \[ \lim_{x \to +\infty} f(x)=k \in \mathbb{R} \quad \left(\lim_{x \to -\infty} f(x)=k \in \mathbb{R}\right), \] ha un asintoto orizzontale di equazione $y=k$ per $x$ che tende a $+\infty$ ($-\infty$).

Sempre in riferimento all’Esempio 3.1, si ha che \[ \lim_{x \to -2^-}\, \frac{x-2}{x+2}=+\infty, \quad \lim_{x \to -2^+}\, \frac{x-2}{x+2}=-\infty. \] In questo caso, è importante notare che \[ \lim_{x \to -2}\, \frac{x-2}{x+2} \; \text{ non esiste}, \] in quanto i rispettivi limiti sinistro e destro sono differenti. La non esistenza del limite è causata dal fatto che la funzione assume valori arbitrariamente grandi a sinistra del punto $x_0=-2$; arbitrariamente piccoli (cioè tendenti a $-\infty$) a destra del punto $x_0=-2$.

È corretto invece affermare che \[ \lim_{x \to -2} \, \left| \frac{x-2}{x+2}\right|=+\infty, \] cioè che nell’intorno di $x_0=-2$ la funzione assume valori arbitrariamente grandi in valore assoluto. In questi casi, si dice che il grafico della funzione ha un asintoto verticale.

Definition 3.5 Diremo che il grafico di una funzione $f$ per cui vale \[ \lim_{x \to x_0} \left| f(x)\right|=+\infty,\; x_0 \in \mathbb{R}, \] ha un asintoto verticale per $x$ che tende a $x_0$.

Anche se una funzione e il suo grafico sono due oggetti matematici distinti, come già osservato nel Capitolo 2, è accettabile dire che una funzione ammette un asintoto (orizzontale, verticale o – come vedremo nel seguito – obliquo) intendendo con questo che lo ammette il suo grafico.

3.4 Limiti in punti di accumulazione non compresi nel dominio (A)

La prima casistica (A) che proponiamo affronta il calcolo dei limiti nel punto o nei punti esclusi dal dominio naturale di una funzione perché annullano il denominatore di una frazione. Quando il numeratore ha limite diverso da zero, in questi casi si ha un asintoto verticale.

Example 3.2 Si consideri la funzione $f: \mathbb{R}\setminus \{2\} \to \mathbb{R}$, definita da \[ f(x)=\frac{x+2}{x-2}. \] Questo è il tipico caso di frazione la cui condizione di esistenza esclude dal dominio naturale della funzione il singolo punto $x_0=2$, dove il denominatore si annulla. In questi casi, è necessario valutare cosa accade alla funzione in un intorno del punto. Si procede come di seguito:

si valuta il limite del numeratore della frazione: se anche il numeratore tende a zero, si deve usare una diversa casistica (la (C) descritta di seguito, o la (D) nel Capitolo 4). Se invece il numeratore della frazione tende ad un numero non nullo, come in questo caso in cui $(x+2) \to 4$, allora appare chiaro che la funzione, in valore assoluto, diventerà arbitrariamente grande essendo il rapporto di un numeratore non nullo e di un denominatore che tende ad annullarsi. Si avrà dunque che \[ \lim_{x \to 2}\, \left| \frac{x+2 \,(\to \mathbf{4})}{x-2 \,(\to \mathbf{0})} \right| = +\infty, \] e il grafico della funzione avrà un asintoto verticale;
per disegnare il grafico della funzione è necessaria però una informazione migliore, ovvero si deve capire se la funzione tende a $+\infty$, a $-\infty$, o varia il suo comportamento negli intorni sinistro o destro del punto in oggetto. A tal fine, è necessario determinare se il denominatore cambia di segno nell’intorno del punto. In questo caso, il denominatore è rappresentato dalla funzione $x-2$, una retta strettamente crescente che, annullandosi in $x=2$, sarà negativa a sinistra di questo punto, e positiva alla sua destra. In conclusione, si ha: \[ \lim_{x \to 2^-}\, \frac{x+2 \,(\mathbf{+})}{x-2 \, (\mathbf{-})} = -\infty, \quad \lim_{x \to 2^+}\, \frac{x+2 \,(\mathbf{+})}{x-2 \, (\mathbf{+})} = +\infty, \] dove si sono messi in evidenza i segni di numeratore e denominatore nei due intorni del punto $x_0=2$. Formalmente, il limite $\lim_{x \to 2}f(x)$ non esiste essendo i limiti sinistro e destro differenti. In modo del tutto analogo si calcolano i limiti nell’Esempio 3.1.

In questa casistica (A) di calcolo di un limite, il segno del numeratore tipicamente permane (grazie al Teorema di Permanenza del Segno) in un intorno sufficientemente piccolo del punto in oggetto. Ai fini dell’esistenza del limite nell’intorno completo, e dell’eventuale differente calcolo dei limiti sinistro e destro, è necessario valutare se il denominatore della funzione cambi o meno il suo segno in tale intorno.

Example 3.3 Si consideri la funzione $f: \mathbb{R}\setminus \{-2,2\} \to \mathbb{R}$, definita da \[ f(x)=\frac{1-x}{x^2-4}. \] In questo esempio sono due i numeri reali sottratti dal dominio naturale della funzione (dove il denominatore della frazione si annulla). Il comportamento in ognuno di essi andrà valutato analogamente all’esempio precedente.

Si inizi con il punto $x_0=-2$. Il numeratore $(1-x)\to 3$, quindi permane positivo in un intorno del punto; il denominatore, una parabola convessa, cambia il segno nell’intorno delle sue radici. Disegnare il grafico di $x^2-4$ aiuta a stabilire che: \[ \lim_{x \to -2^-} \,\frac{1-x \,\,\,(\mathbf{+})}{x^2-4 \, (\mathbf{+})} = +\infty, \quad \lim_{x \to -2^+} \,\frac{1-x \,\,\,(\mathbf{+})}{x^2-4 \, (\mathbf{-})} = -\infty. \]

Si osservi come sia fondamentale conoscere il comportamento delle funzioni elementari per identificare correttamente i loro cambiamenti di segno nell’intorno delle loro radici. Un errore frequente è quello di ritenere frettolosamente che una funzione che si annulla in un punto sia negativa a sinistra e positiva a destra di esso. Ciò dipende, naturalmente, dalle proprietà di monotonia della funzione nell’intorno del punto.

Si prosegua quindi con l’analisi del punto $x_0=2$. Il numeratore $(1-x)\to -1$, quindi permane negativo in un intorno del punto; il denominatore cambia il suo segno. Analogamente a prima si ha quindi: \[ \lim_{x \to 2^-} \,\frac{1-x \,\,\,(\mathbf{-})}{x^2-4 \, (\mathbf{-})} = +\infty, \quad \lim_{x \to 2^+} \,\frac{1-x \,\,\,(\mathbf{-})}{x^2-4 \, (\mathbf{+})} = -\infty. \]

Example 3.4 Si consideri la funzione $f: \mathbb{R}\setminus \{1\} \to \mathbb{R}$, definita da \[ f(x)=\frac{3-4x}{(1-x)^2}. \] In questo esempio, nell’intorno di $x_0=1$, si ha $(3-4x) \to -1$, e il numeratore permane negativo. È immediato vedere che il denominatore della frazione, essendo un quadrato, è sempre non negativo (su tutto il dominio della funzione). Si ha quindi l’esistenza del limite completo \[ \lim_{x \to 1} \,\frac{3-4x \,\,\,\,\,(\mathbf{-})}{(1-x)^2 \, (\mathbf{+})} = -\infty. \]

Example 3.5 Si consideri la funzione $f: \mathbb{R}\setminus \{1\} \to \mathbb{R}$, definita da \[ f(x)=\frac{3-4x}{(1-x)^3}. \] Rispetto all’esempio precedente, si osservi come il denominatore, potenza dispari, cambi il suo segno nell’intorno del punto $x_0=1$. In particolare, il denominatore è una funzione strettamente decrescente, quindi assumerà valori positivi a sinistra del punto e negativi a destra. In questo caso, i limiti sinistro e destro saranno quindi differenti: \[ \lim_{x \to 1^-} \,\frac{3-4x \,\,\,\,(\mathbf{-})}{(1-x)^3 \, (\mathbf{+})} = -\infty, \quad \lim_{x \to 1^+} \,\frac{3-4x \,\,\,\,(\mathbf{-})}{(1-x)^3 \, (\mathbf{-})} = +\infty. \]

3.5 Funzioni continue

Nella sezione precedente abbiamo supposto di saper calcolare alcuni limiti intuitivamente chiari come \[ \lim_{x \to 2} \,x+2 = 4. \] Probabilmente, abbiamo mentalmente sostituito il valore $x=2$ alla funzione, ricavando il fatto che \[ \lim_{x \to 2} \,x+2 = (2)+2 = 4. \] Anche se intuitivo, questo procedimento sfrutta di fatto la proprietà di continuità della funzione $(x+2)$.

Definition 3.6 Una funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$ si dice continua nel punto $x_0 \in A$ se \[ \lim_{x \to x_0}f(x)=f(x_0). \] Se $f$ è continua in ogni $x_0 \in A$, si dice che $f$ è continua su $A$.

Remark. Osserviamo i seguenti punti fondamentali sulla definizione di continuità:

il concetto di continuità traduce l’idea che una funzione $f$, in un intorno del punto $x=x_0$, stia vicina al valore $f(x_0)$ assunto in quel punto. Equivalentemente, che il limite della funzione nel punto si possa calcolare semplicemente sostituendo il valore $x=x_0$ nella funzione;
per essere continua in un punto, una funzione deve essere ben definita in quel punto (ad esempio, la funzione dell’Esempio 3.1 non è continua nel punto $x=-2$);
per definizione di limite, la definizione ha senso solo se $x_0 \in A$ è un punto di accumulazione per $A$;
al contrario del limite, che non dipende da ciò che accade nel punto in cui lo si calcola, l’essere continua dipende anche da ciò che accade nel punto. In particolare una funzione $f$ è continua nel punto $x=x_0$ se sono verificate tutte le seguenti condizioni:
- la funzione è ben definita in quel punto;
- esistono finiti sia il limite sinistro che il limite destro della funzione in quel punto;
- il limite sinistro e il limite destro sono uguali tra loro e uguali al valore della funzione in quel punto;
in virtù di quanto appena espresso, il grafico di una funzione continua su un intervallo è connesso, ovvero si può disegnare senza punti di interruzione, continuamente appunto;
è facile dimostrare che tutte le funzioni elementari studiate sino a questo punto (funzioni lineari, quadratiche, potenze, valore assoluto, logaritmo ed esponenziale) sono continue sul loro dominio naturale. Sono quindi giustificati tutti i passaggi svolti nel calcolo dei limiti di tipologia (A);
grazie al Teorema 3.4 è immediato dimostrare che la somma, il prodotto, il quoziente e la composizione di funzioni elementari sono continue sui propri domini naturali. In conclusione, qualsiasi funzione venga prodotta attraverso queste operazioni a partire dalle funzioni elementari studiate è continua laddove è ben definita.

Chiarifica ulteriormente il concetto di continuità, l’elencare i casi in cui una funzione non è continua in un particolare punto. Si possono verificare tre tipologie di discontinuità:

si verifica una discontinuità eliminabile se esistono finiti sia il limite sinistro che il limite destro della funzione in un punto, essi sono uguali tra loro ma differenti dal valore della funzione in quel punto. Si prenda ad esempio la funzione $f:\mathbb{R}\to \mathbb{R},$ \[ f(x)= \begin{cases} \frac{x}{x}, &\text{ se } x \neq 0;\\ 0, &\text{ se } x = 0. \end{cases} \]

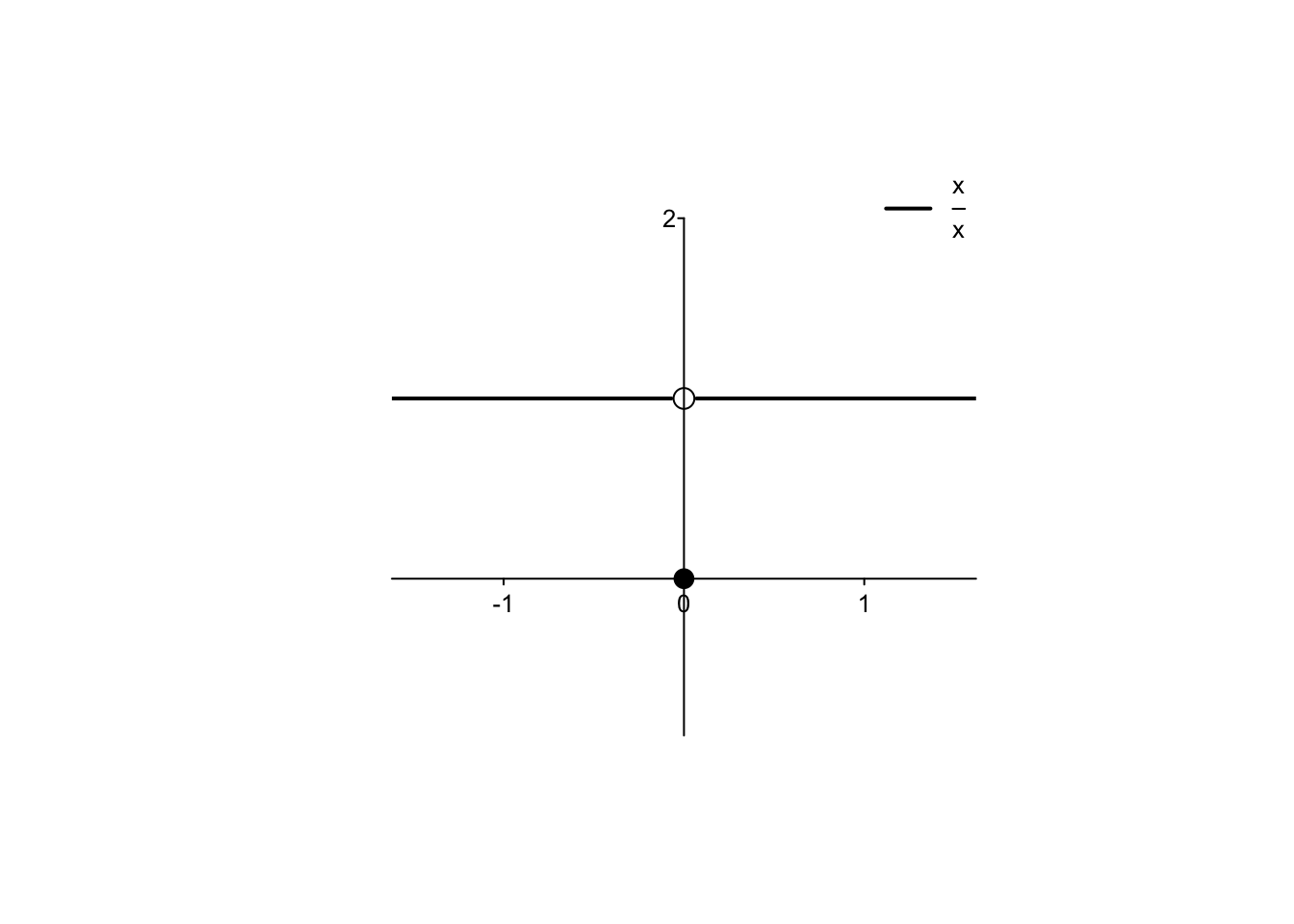
Dato che $\lim_{x\to 0}f(x)=1$, è sufficiente cambiare la definizione definendo $f(0)=1$ per rendere la funzione definita su tutto l’asse reale e ivi continua;

si verifica una discontinuità di prima specie se esistono finiti sia il limite sinistro che il limite destro della funzione in un punto, ma essi non sono coincidenti. Si prenda ad esempio la funzione $f:\mathbb{R} \to \mathbb{R},$ \[ f(x)= \begin{cases} \frac{x}{|x|}, &\text{se $x \neq 0$;} \\ 1, &\text{se $x = 0$.} \end{cases} \]

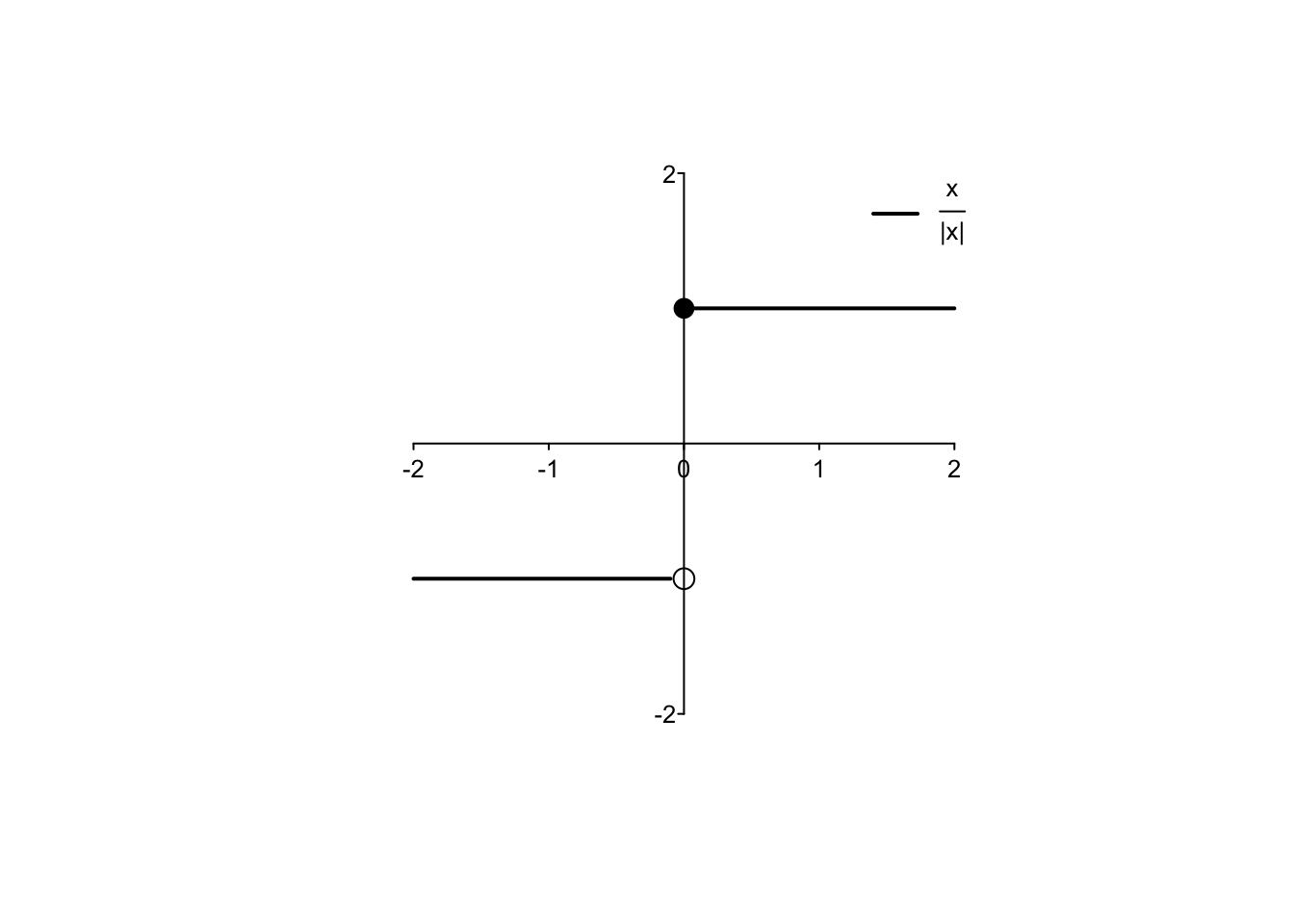In questo caso, $\lim_{x \to 0^-}f(x)=-1 \neq 1=\lim_{x \to 0^+}f(x)$ e la discontinuità non è eliminabile nemmeno variando il valore assunto dalla funzione nel punto $x=0$;

si verifica una discontinuità di seconda specie se almeno uno tra i limiti sinistro e destro della funzione non esiste o è infinito. Si prenda ad esempio la funzione $f:\mathbb{R} \to \mathbb{R},$ \[ f(x)= \begin{cases} 2, &\text{se $x \leq -2$;} \\ \frac{x-2}{x+2}, &\text{se $x > -2$.} \end{cases} \]

Tale funzione è discontinua nel punto $x=-2$, in quanto $\lim_{x \to -2^+}f(x)=-\infty$.

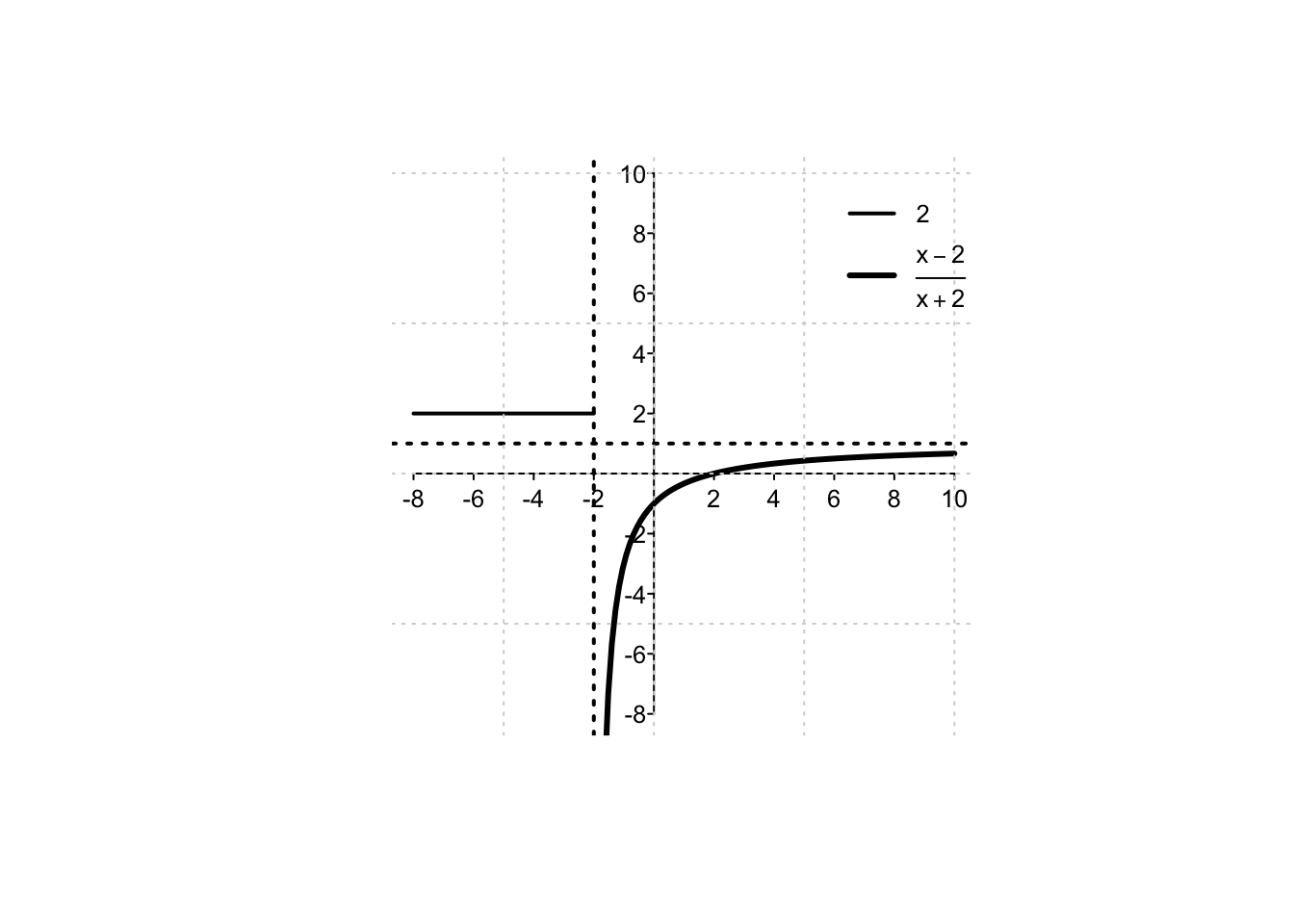
Chiaramente, come per una discontinuità di prima specie, una discontinuità di seconda specie non è eliminabile.

3.6 Limite del quoziente di funzioni infinite (B)

Una seconda casistica (B) di calcolo dei limiti comprende il calcolo di quozienti di funzioni infinite, ovvero di funzioni che nell’intorno di un punto tendono a diventare, in valore assoluto, arbitrariamente grandi.

Definition 3.7 Una funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$ si dice infinita per $x$ che tende a $x_0 \in \mathbb{R}^*$, punto di accumulazione per $A$, se \[\lim_{x \to x_0} \left| f(x) \right| = +\infty.\]

Ricordando le operazioni possibili con gli infiniti, introdotte nel Capitolo 1, il quoziente di funzioni infinite dà luogo ad una forma indeterminata del tipo \[ \frac{\pm \infty}{\pm \infty}. \] Una tale forma indeterminata è facilmente risolvibile identificando al numeratore e al denominatore le funzioni che tendono all’infinito più velocemente delle altre.

Example 3.6 Si calcoli \[ \lim_{x \to +\infty} \,\frac{2x^5+3x^3}{4x^4+2x}. \] Quella in oggetto è una forma indeterminata del tipo $\frac{+\infty}{+\infty}$. Per risolverla basta mettere in evidenza il termine che più velocemente tende all’infinito sia al numeratore che, separatamente, al denominatore. Sfruttando le proprietà dei limiti (Teorema 3.4), si ottiene: \[ \lim_{x \to +\infty}\, \frac{2x^5+3x^3}{4x^4+2x}= \lim_{x \to +\infty}\, \frac{x^5\left(2+\frac{3}{x^2}\right)}{x^4\left(4+\frac{2}{x^3}\right)}=\lim_{x \to +\infty}\,x\;\frac{\left(2+\frac{3}{x^2}\right)}{\left(4+\frac{2}{x^3}\right)}= +\infty \, \frac{(2+0)}{(4+0)}= +\infty. \] In modo del tutto analogo, si possono calcolare i limiti \[ \lim_{x \to +\infty}\, \frac{2x^4+3x^3}{4x^4+2x}= \lim_{x \to +\infty} \,\frac{x^4\left(2+\frac{3}{x}\right)}{x^4\left(4+\frac{2}{x^3}\right)}=\lim_{x \to +\infty}\,\frac{\left(2+\frac{3}{x}\right)}{\left(4+\frac{2}{x^3}\right)}= \, \frac{(2+0)}{(4+0)}= \frac{1}{2}, \]

\[ \lim_{x \to +\infty} \,\frac{2x^5+3x^3}{4x^6+2x}= \lim_{x \to +\infty}\, \frac{x^5\left(2+\frac{3}{x^2}\right)}{x^6\left(4+\frac{2}{x^5}\right)}=\lim_{x \to +\infty}\,\frac{1}{x}\;\frac{\left(2+\frac{3}{x^2}\right)}{\left(4+\frac{2}{x^5}\right)}= \frac{1}{+\infty} \, \frac{(2+0)}{(4+0)}=0 \,\frac{2}{4} =0. \]

È importante osservare come, nel calcolo dei tre limiti dell’esempio precedente, siano rilevanti, al numeratore e al denominatore, esclusivamente i polinomi di grado più alto, che si dicono avere un ordine di infinito più grande degli altri.

Definition 3.8 Siano $f,g$ due funzioni infinite per $x$ che tende a $x_0\in \mathbb{R}^*$.

Se $\lim_{x \to x_0} \left| \frac{f(x)}{g(x)}\right| =+\infty$, si dice che $f$ è infinita di ordine superiore a $g$.
Se $\lim_{x \to x_0} \frac{f(x)}{g(x)}= k \in \mathbb{R} \setminus \{0\}$, si dice che $f$ è infinita di ordine uguale a $g$.
Se $\lim_{x \to x_0} \frac{f(x)}{g(x)} = 0$, si dice che $f$ è infinita di ordine inferiore a $g$.

È equivalente affermare che una funzione $f$ è infinita di ordine superiore ad un’altra funzione $g$, oppure affermare che l’ordine di infinito di $f$ è superiore a quello di $g$. Alterneremo arbitrariamente le due dizioni nel seguito. Se $f$ ha lo stesso ordine di infinito di $g$, si scrive anche $f=O(g)$.

Il seguente teorema formalizza il procedimento usato per risolvere le forme indeterminate del tipo $\frac{\pm \infty}{\pm \infty}$ nell’Esempio 3.6.

Theorem 3.5 (Confronto degli Ordini di Infinito) Siano $f,F,g,G$ quattro funzioni infinite per $x \to x_0 \in \mathbb{R}^*$, con:

$F$ infinita di ordine superiore rispetto a $f$;
$G$ infinita di ordine superiore rispetto a $g$.

Si ha allora che

\[ \lim_{x \to x_0} \frac{F(x)+f(x)}{G(x)+g(x)}= \lim_{x \to x_0} \frac{F(x)\left(1+\frac{f(x)}{F(x)}\right)}{G(x)\left(1+\frac{g(x)}{G(x)}\right)}= \lim_{x \to x_0} \frac{F(x)}{G(x)}. \]

Remark. Osserviamo i seguenti punti fondamentali riguardo al Teorema del Confronto degli Ordini di Infinito:

il teorema si applica alle funzioni infinite, quindi non solo per $x \to \pm \infty$: una funzione può essere infinita nell’intorno di qualsiasi punto $x_0 \in \mathbb{R}^*$;
il teorema si applica analogamente anche alla somma di un qualsiasi numero finito di funzioni infinite, mettendo in evidenza una qualsiasi tra di esse che abbia un ordine di infinito maggiore o uguale a tutte le altre;
si osservi (ancora) come, nella formula dell’enunciato del Teorema, non ci sia bisogno di discutere l’esistenza dei denominatori: essendo le funzioni infinite, in un intorno sufficientemente piccolo del punto $x_0$ esse saranno positive o negative, quindi non nulle.

È immediato verificare che, all’infinito, un polinomio di grado $n$ (definito in (2.1)) è una funzione infinita di ordine superiore rispetto ad un polinomio di grado $m$ se e solo se $n>m$; i due polinomi avranno lo stesso ordine di infinito se $n=m$.

Applicando il Teorema della Gerarchia degli Infiniti all’Esempio 3.1 si calcola: \[ \lim_{x \to \pm\infty}\, \frac{x-2}{x+2}=\lim_{x \to \pm\infty} \,\frac{x}{x} =1, \] dove con $x \to \pm \infty$ indicheremo nel seguito che lo stesso limite vale sia per $x \to +\infty$ che per $x \to -\infty$.

Per trattare altre forme indeterminate del tipo $\frac{\pm \infty}{\pm \infty}$, è necessario sapere come si comportano rispetto alle potenze le funzioni logaritmo ed esponenziale. Dal grafico di queste funzioni, si deduce la gerarchia degli infiniti enunciata nel seguente Teorema.

Theorem 3.6 Per $x \to +\infty$, si ha che:

la funzione esponenziale è infinita di ordine superiore a qualsiasi potenza, ovvero \[ \lim_{x \to +\infty} \,\frac{e^x}{x^q}= +\infty, \quad q \in \mathbb{Q},\, q>0; \]
la funzione logaritmo è infinita di ordine inferiore a qualsiasi potenza, ovvero \[ \lim_{x \to +\infty}\, \frac{\log (x)}{x^q}= 0, \quad q \in \mathbb{Q},\, q>0. \]

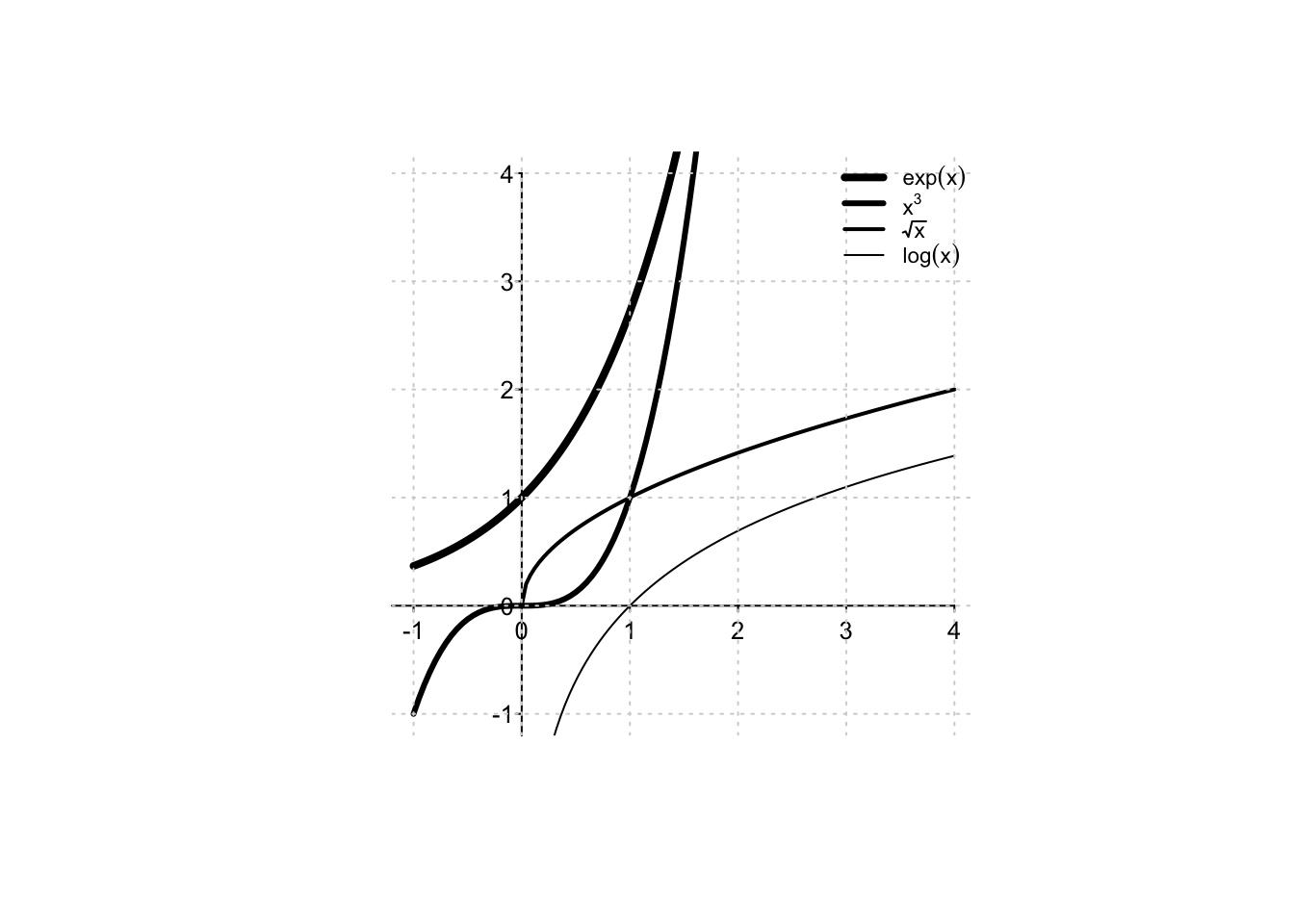
Conoscendo la gerarchia degli ordini di infinito appena enunciata, i limiti nella forma $\frac{\pm \infty}{\pm \infty}$ si riducono di fatto ad un immediato confronto delle funzioni che al numeratore e al denominatore di un quoziente hanno ordine di infinito superiore.

Example 3.7 Si calcolino i seguenti limiti.

Si calcoli \[ \lim_{x \to +\infty} \,\frac{x^4-3x^2+x}{2x^4+4x^2+\log(x^2)}=\lim_{x \to +\infty} \,\frac{x^4}{2x^4}=\lim_{x \to +\infty} \,\frac{1}{2}=\frac{1}{2}. \]

Il Teorema del Confronto degli Ordini di Infinito permette, al limite, di cancellare le funzioni con ordine di infinito inferiore per poi procedere ad una ordinaria semplificazione. Si osservi come l’ordine di infinito del logaritmo di una potenza rimanga lo stesso del logaritmo, $\log(x^2)=2\log (x)$.

Si calcoli \[ \lim_{x \to -\infty}\,\frac{x^4-3x^2+x}{2x^3+4x^2+\log(x^2)}=\lim_{x \to -\infty} \,\frac{x^4}{2x^3}= \lim_{x \to -\infty} \,\frac{x}{2}=-\infty. \]

L’applicazione del Teorema del Confronto degli Ordini di Infinito non dipende dal punto $x_0$ in cui viene calcolato il limite, in questo caso $x_0=-\infty$, ma solo dal fatto che le funzioni siano infinite. Si osservi come l’ordine di infinito di una potenza sia lo stesso sia a $+\infty$ che a $-\infty$, $x^4=(-x)^4$, $x^3=-(-x)^3$.

Si calcoli \[ \lim_{x \to +\infty} \,\frac{x^3-2}{4x^3-2e^x}=\lim_{x \to +\infty}\, \frac{x^3}{-2e^x}=0. \]
Si calcoli \[ \lim_{x \to -\infty}\, \frac{x^3-2}{4x^3-2e^x}=\lim_{x \to -\infty}\, \frac{x^3}{4x^3-0}=\frac{1}{4}. \]

Si presti particolare attenzione al fatto che la funzione esponenziale è infinita per $x \to +\infty$, ma tende a zero (è infinitesima) per $x \to -\infty$.

Si calcoli \[ \lim_{x \to -\infty} \,\frac{\log(|x|)-2}{\log(|x|^5)-\sqrt{|x|}}=\lim_{x \to -\infty} \,\frac{\log(|x|)}{-\sqrt{|x|}}=0. \]

Si osservi come le funzioni pari come $\log|x|, \sqrt{|x|}$, essendo simmetriche, hanno lo stesso ordine di infinito per $x \to \pm \infty$.

3.7 Limite della differenza di funzioni infinite (B2)

Il Teorema del Confronto degli Ordini di Infinito può essere applicato anche al limite di una differenza. Se $f,F$ sono due funzioni infinite per $x \to x_0$, con $F$ infinita di ordine superiore a $f$, si avrà cioè \[ \lim_{x \to x_0} F(x)-f(x) = \lim_{x \to x_0} F(x)\left(1-\frac{f(x)}{F(x)}\right)= \lim_{x \to x_0} F(x). \]

Example 3.8 Si calcolino \[\begin{align*} \lim_{x \to +\infty} \sqrt{x}-x=\lim_{x \to +\infty} -x=-\infty, \\ \\ \lim_{x \to +\infty} x^5-\frac{2}{3}x=\lim_{x \to +\infty} x^5=+\infty. \end{align*}\]

Diverso è il caso in cui si abbia una differenza di funzioni aventi lo stesso ordine di infinito. In questa situazione non è possibile calcolare immediatamente il limite ma è necessaria una analisi più approfondita.

Example 3.9 Si calcoli \[ \lim_{x \to +\infty} 2x+3-\sqrt{4x^2+x}. \] In questo limite si ha la differenza tra due funzioni $f(x)=2x+3$ e $g(x)=\sqrt{4x^2+x}$ aventi lo stesso ordine di infinito $O(2x)$: \[ \lim_{x \to +\infty}\, \frac{2x+3}{\sqrt{4x^2+x}}=\lim_{x \to +\infty}\, \frac{2x}{\sqrt{4x^2}}=\lim_{x \to +\infty} \,\frac{2x}{2x}=1. \] In questi casi si potrebbe essere portati a dire che il limite della differenza è pari a 0. In generale, questo non è vero.

Nel caso in questione, sfruttando la formula $(f-g)(f+g)=f^2-g^2$ si ottiene: \[\begin{align*} &\lim_{x \to +\infty} (2x+3)-\left(\sqrt{4x^2+x}\right)\\ =&\lim_{x \to +\infty} \,(2x+3)-\left(\sqrt{4x^2+x}\right) \frac{(2x+3)+\left(\sqrt{4x^2+x}\right)}{(2x+3)+\left(\sqrt{4x^2+x}\right)}\\ \\ =&\lim_{x \to +\infty} \,\frac{(2x+3)^2-(4x^2+x)}{2x+3+\sqrt{4x^2+x}}=\lim_{x \to +\infty} \,\frac{4x^2+12x+9-4x^2-x}{2x+3+\sqrt{4x^2+x}}\\ \\ =&\lim_{x \to +\infty}\,\frac{11x+9}{2x+3+\sqrt{4x^2+x}}=\lim_{x \to +\infty}\,\frac{11x}{2x+\sqrt{4x^2}}=\lim_{x \to +\infty}\,\frac{11x}{2x+2x}=\frac{11}{4}. \end{align*}\]

Prima di calcolare un limite è sempre necessario verificare che esso non sia immediatamente calcolabile tramite le proprietà dei limiti e delle funzioni continue. Se il limite si presenta invece in una forma indeterminata, calcolarlo significa in pratica riscrivere il suo argomento in modo tale da farlo diventare una forma determinata, come avvenuto nell’esempio precedente.

3.8 Limite del quoziente di funzioni infinitesime (C)

Una terza casistica (C) di calcolo dei limiti si occupa delle forme indeterminate del tipo $\frac{0}{0}$, ovvero dei rapporti tra funzioni infinitesime.

Definition 3.9 Una funzione $f:A \subseteq \mathbb{R} \to \mathbb{R}$ si dice infinitesima per $x$ che tende a $x_0 \in \mathbb{R}^*$, punto di accumulazione per $A$, se \[\lim_{x \to x_0} f(x) = 0.\]

È triviale osservare che, se si cambia il punto in cui si calcola il limite di una stessa funzione, il risultato (e il comportamento della funzione) sarà differente. Si osservi ad esempio che

\[ \lim_{x \to +\infty} \,\frac{2x^3+4x^5}{4x^3+5x^4}=\lim_{x \to +\infty} \,\frac{4x^5}{5x^4}= \lim_{x \to +\infty} \,\frac{4}{5}x=+\infty, \]

mentre, per $x \to 0$, la stessa funzione ha limite \[ \lim_{x \to 0} \,\frac{2x^3+4x^5}{4x^3+5x^4}=\lim_{x \to 0}\, \frac{x^3(2 +4x^2)}{x^3(4+5x)}=\lim_{x \to 0}\, \frac{2 +4x^2}{4+5x}=\frac{2+0}{4+0}=\frac{1}{2}. \] Per risolvere una forma indeterminata del tipo $\frac{0}{0}$, è utile ricordare il seguente teorema sui polinomi del tipo (2.1).

Theorem 3.7 (Teorema di Ruffini) Un polinomio $P(x)$ è divisibile per $(x-x_0)$, ovvero si può esprimere come $P(x)=(x-x_0)Q(x)$, con $Q(x)$ polinomio di grado inferiore, se e solo se $P(x_0)=0$.

Il seguente esempio illustra come utilizzare questo risultato nella risoluzione di forme indeterminate di tipo (C).

Example 3.10 Si calcoli \[ \lim_{x \to 1}\, \frac{x^2+2x-3}{2x^3-x-1}. \] Nella funzione argomento del limite, sia il numeratore che il denominatore si annullano nel punto $x_0=1$, dando luogo ad una forma indeterminata di tipo (C) ma nel contempo rivelando (Teorema di Ruffini) che entrambi sono divisibili per $(x-1)$.

Per quanto riguarda il numeratore, ricordando che $(x+a)(x+b)=x^2+(a+b)x+ab$, si avrà che $x^2+2x-3=(x-1)(x+3)$.

Per quanto riguarda il denominatore, che sappiamo essere scomponibile come $2x^3-3x+1 =(x-1)Q(x)$, si osservi che il termine di grado più alto di $Q(x)$ deve essere forzatamente il monomio $2x^2$, ovvero \[ 2x^3-x-1 =(x-1)(2x^2+R(x)). \] Dato che $(x-1)2x^2=2x^3-2x^2$, e che il polinomio a sinistra del segno di $=$ non contiene termini di grado 2, $R(x)$ dovrà quindi contenere il termine $2x$, ovvero \[ 2x^3-x-1 =(x-1)(2x^2+2x+S(x)). \] Analogamente, essendo $(x-1)(2x^2+2x)=2x^3-2x^2+2x^2-2x=2x^3-2x$, dovrà essere $S(x)=1$: \[ 2x^3-x-1 =(x-1)(2x^2+2x+1). \]

Si potrà allora scrivere \[\begin{align*} \lim_{x \to 1}\, \frac{x^2+2x-3}{2x^3-x-1} &=\lim_{x \to 1}\, \frac{(x-1)(x+3)}{(x-1)(2x^2+2x+1)}\\&=\lim_{x \to 1}\, \frac{(x+3)}{(2x^2+2x+1)}=\frac{1+3}{2+2+1}=\frac{4}{5}. \end{align*}\] Dato che questo limite esiste (e quindi esistono i corrispondenti limiti sinistro e destro), ma il punto $x=1$ è escluso dal dominio della funzione argomento del limite, ne segue che tale funzione può essere estesa attribuendo al punto $x=1$ l’immagine $f(1)=\frac{4}{5}$ per farne una funzione continua su tutto l’asse reale.

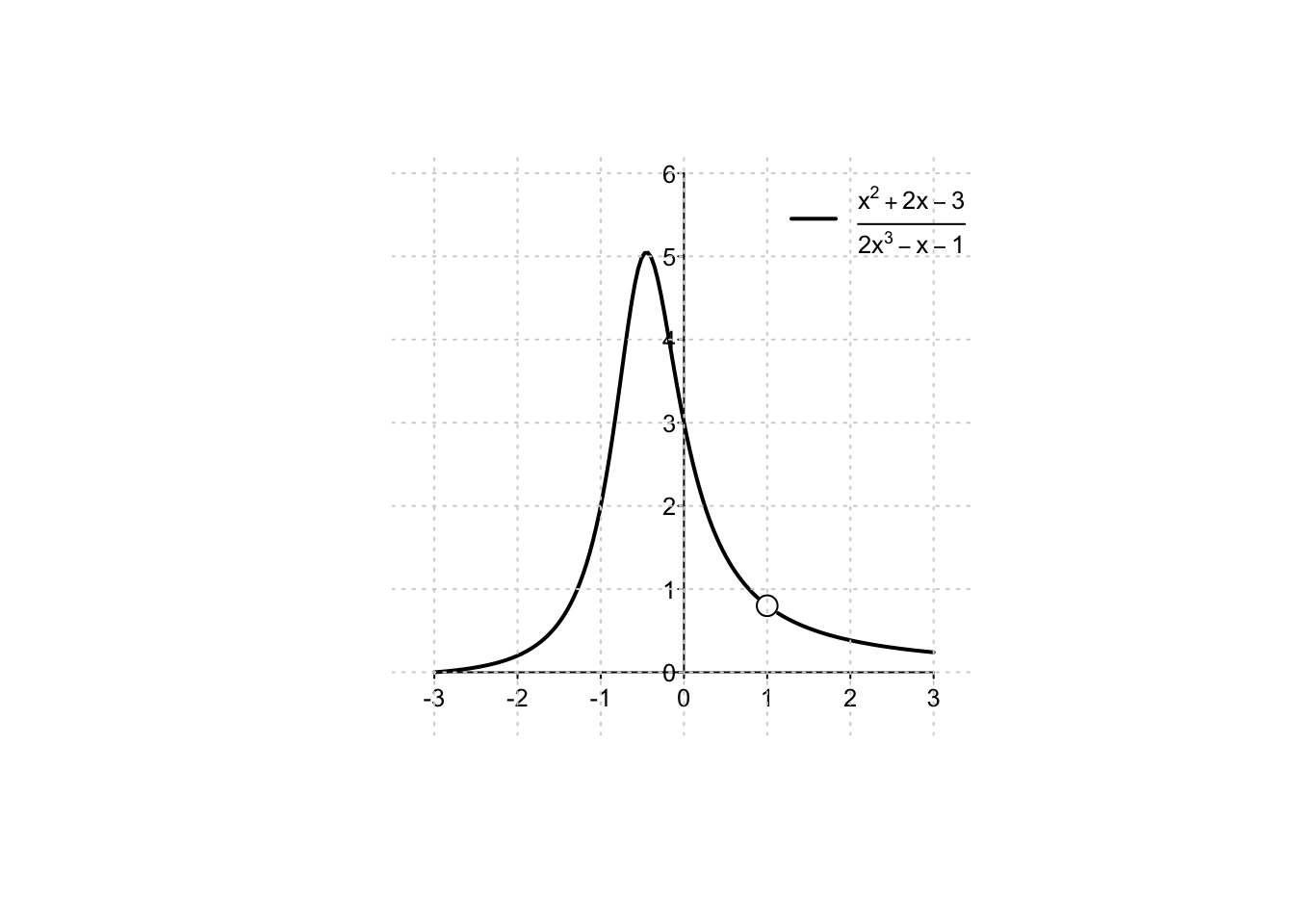
Nel calcolare il limite per $x \to x_0$ del rapporto di due polinomi che si annullano proprio in $x=x_0$, è possibile dividere entrambi i polinomi per $(x-x_0)\neq 0$ e ridursi così ad una forma determinata, oppure ad un’altra forma $\frac{0}{0}$ in cui effettuare una nuova divisione. Si osservi come la divisione di numeratore e denominatore per $(x-x_0)$ sia possibile in quanto, nel calcolare un limite per $x \to x_0$, il punto $x=x_0$ risulti escluso. Si ha quindi $(x-x_0)\neq 0$.

Il procedimento descritto nell’esempio precedente per effettuare la divisione di un polinomio $P(x)$ per $(x-x_0)$ può essere applicato (grazie al Teorema di Ruffini) a qualsiasi polinomio per cui $P(x_0)=0$.

Example 3.11 Si calcoli \[ \lim_{x \to 2} \,\frac{x^2-3x+2}{x^2-4x+4}. \] Il limite presenta una forma indeterminata del tipo $\frac{0}{0}$. Procedendo analogamente all’esempio precedente, ed osservando che al denominatore dell’argomento del limite si trova un quadrato, si calcola facilmente che \[ \lim_{x \to 2} \,\frac{(x-2)(x-1)}{(x-2)^2}=\lim_{x \to 2}\, \frac{x-1 \,(\to \mathbf{1})}{x-2 \,(\to \mathbf{0})}. \] La divisione per $(x-2)$ ha ricondotto un limite di tipo (C) ad un limite di tipo (A). Osservando che $(x-2)$ è una funzione strettamente crescente si avrà \[ \lim_{x \to 2^-}\, \frac{x-1 \,(\mathbf{+})}{x-2 \,(\mathbf{-})}=-\infty, \quad \lim_{x \to 2^+} \,\frac{x-1 \,(\mathbf{+})}{x-2 \,(\mathbf{+})}=+\infty. \]

Example 3.12 Si calcoli \[ \lim_{x \to 2} \,\frac{1-\sqrt{x-1}}{x^2-4}. \] Il limite presenta una forma indeterminata del tipo $\frac{0}{0}$. In presenza di una radice quadrata, si può provare a razionalizzare l’argomento del limite procedendo analogamente all’Esempio 3.9. Si ottiene quindi: \[\begin{align*} \lim_{x \to 2}\, \frac{1-\sqrt{x-1}}{x^2-4}&=\lim_{x \to 2}\, \frac{(1-\sqrt{x-1})}{(x^2-4)}\frac{(1+\sqrt{x-1})}{(1+\sqrt{x-1})}=\lim_{x \to 2} \,\frac{1-(x-1)}{(x^2-4)(1+\sqrt{x-1})} \\ \\ &=\lim_{x \to 2}\, \frac{(2-x)}{(x^2-4)(1+\sqrt{x-1})}=\lim_{x \to 2}\, \frac{(2-x)}{(x+2)(x-2)(1+\sqrt{x-1})} \\ \\ &=\lim_{x \to 2}\, \frac{-1}{(x+2)(1+\sqrt{x-1})}=\frac{-1}{4 \cdot 2}=-\frac{1}{8}. \end{align*}\]

3.9 Asintoti obliqui

Ricordiamo che il grafico di una funzione $f$ ha un asintoto orizzontale di equazione $y=k, k \in \mathbb{R},$ per $x$ che tende a $+\infty$ ($-\infty$) se \[ \lim_{x \to +\infty} f(x)=k \quad \left(\lim_{x \to -\infty} f(x)=k \right). \]

In tal caso, il grafico della funzione si avvicinerà per $x \to +\infty$ ($-\infty$) a quello di una retta orizzontale. È possibile generalizzare questo comportamento includendo la possibilità di avvicinarsi al grafico di una qualsiasi retta. In questo caso si parla di asintoto obliquo.

Definition 3.10 Diremo che il grafico di una funzione $f$ ha un asintoto obliquo di equazione $y=mx+q$, $m,q \in \mathbb{R}$, per $x$ che tende a $+\infty$, se sono verificate le seguenti condizioni:

\[\begin{align*} &\text{1)} \quad \lim_{x \to +\infty} \,\frac{f(x)}{x} =m, \; m \neq 0, \\ \\ &\text{2)} \quad \lim_{x \to +\infty}\, f(x)-mx=q. \end{align*}\]

Analoga definizione vale per $x \to -\infty$.

È immediato verificare che una funzione deve essere infinita per poter ammettere un asintoto obliquo con $m \neq 0$. Se la funzione non è infinita, è inutile controllare le due condizioni.

Un asintoto orizzontale è un tipo particolare di asintoto obliquo che si otterrebbe ammettendo il caso $m=0$ nelle due condizioni della definizione.

Concludiamo questo capitolo illustrando il calcolo degli asintoti obliqui per tre funzioni di interesse.

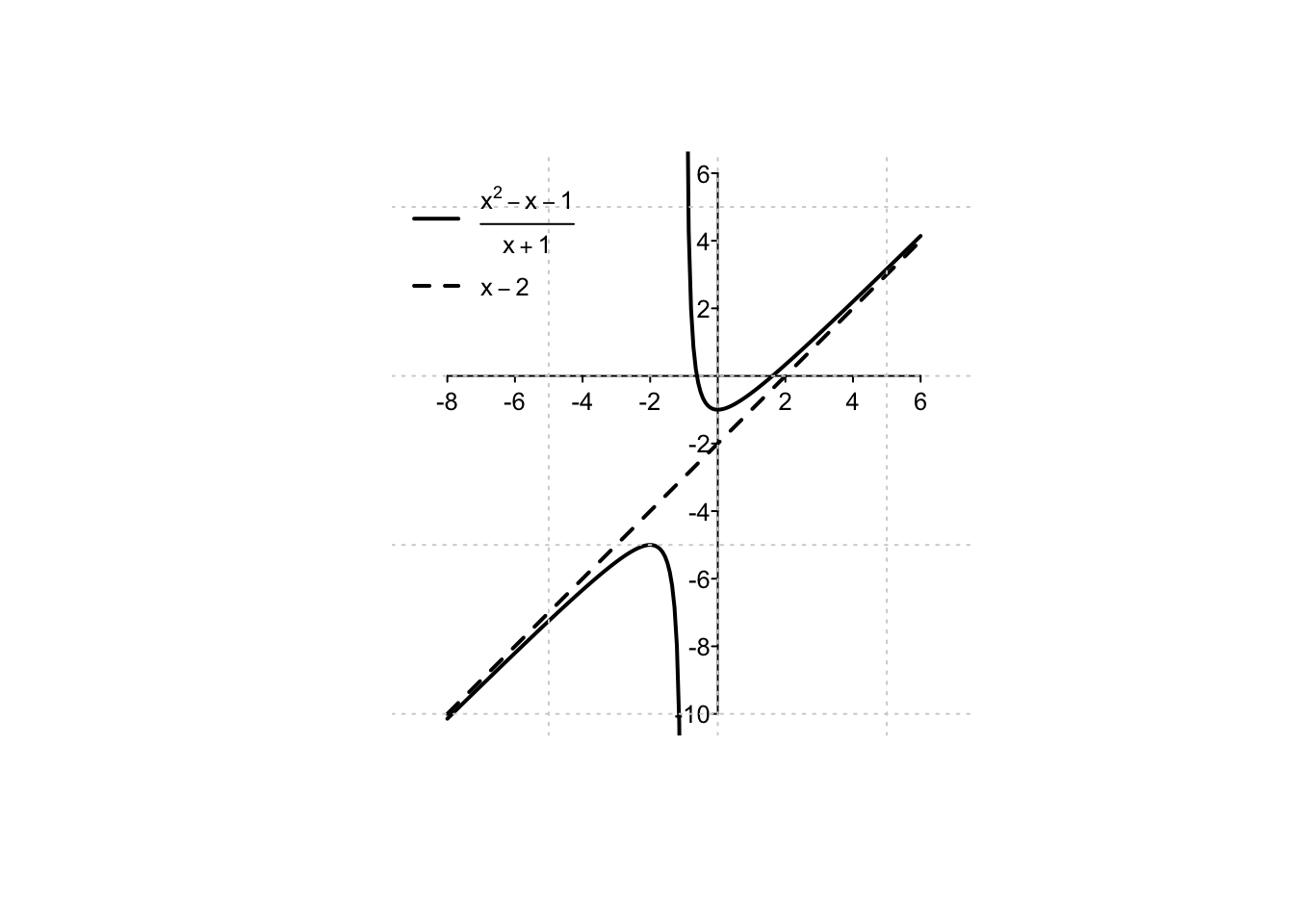
Example 3.13 Si trovino gli eventuali asintoti obliqui della funzione $f:\mathbb{R}\setminus\{-1\}\to \mathbb{R},$ \[ f(x)=\frac{x^2-x-1}{x+1}. \] Si verifica immediatamente che la condizione 1) nella definizione di asintoto obliquo è soddisfatta per $x \to +\infty$ (limite di tipo (B)): \[ \lim_{x \to +\infty} \,\frac{f(x)}{x}=\lim_{x \to +\infty}\, \frac{x^2-x-1}{x^2+x}=\lim_{x \to +\infty}\, \frac{x^2}{x^2}=1=m. \] La seconda condizione tipicamente è più complessa da verificare perché presenta per sua definizione una differenza di funzioni infinite dello stesso ordine (B2): \[\begin{align*} &\lim_{x \to +\infty} f(x)-mx=\lim_{x \to +\infty}\, \frac{x^2-x-1}{x+1}-x \\=&\lim_{x \to +\infty}\, \frac{x^2-x-1-x^2-x}{x+1}=\lim_{x \to +\infty} \,\frac{-2x-1}{x+1}=-2=q. \end{align*}\] Per $x \to +\infty$, il grafico della funzione presenta un asintoto obliquo di equazione $y=x-2$.

Si può verificare (anche mediante il grafico di seguito) che gli stessi calcoli (e quindi lo stesso asintoto) valgono anche per $x \to -\infty$ (come vedremo negli esempi successivi, non sempre gli asintoti sono identici a $\pm \infty$).

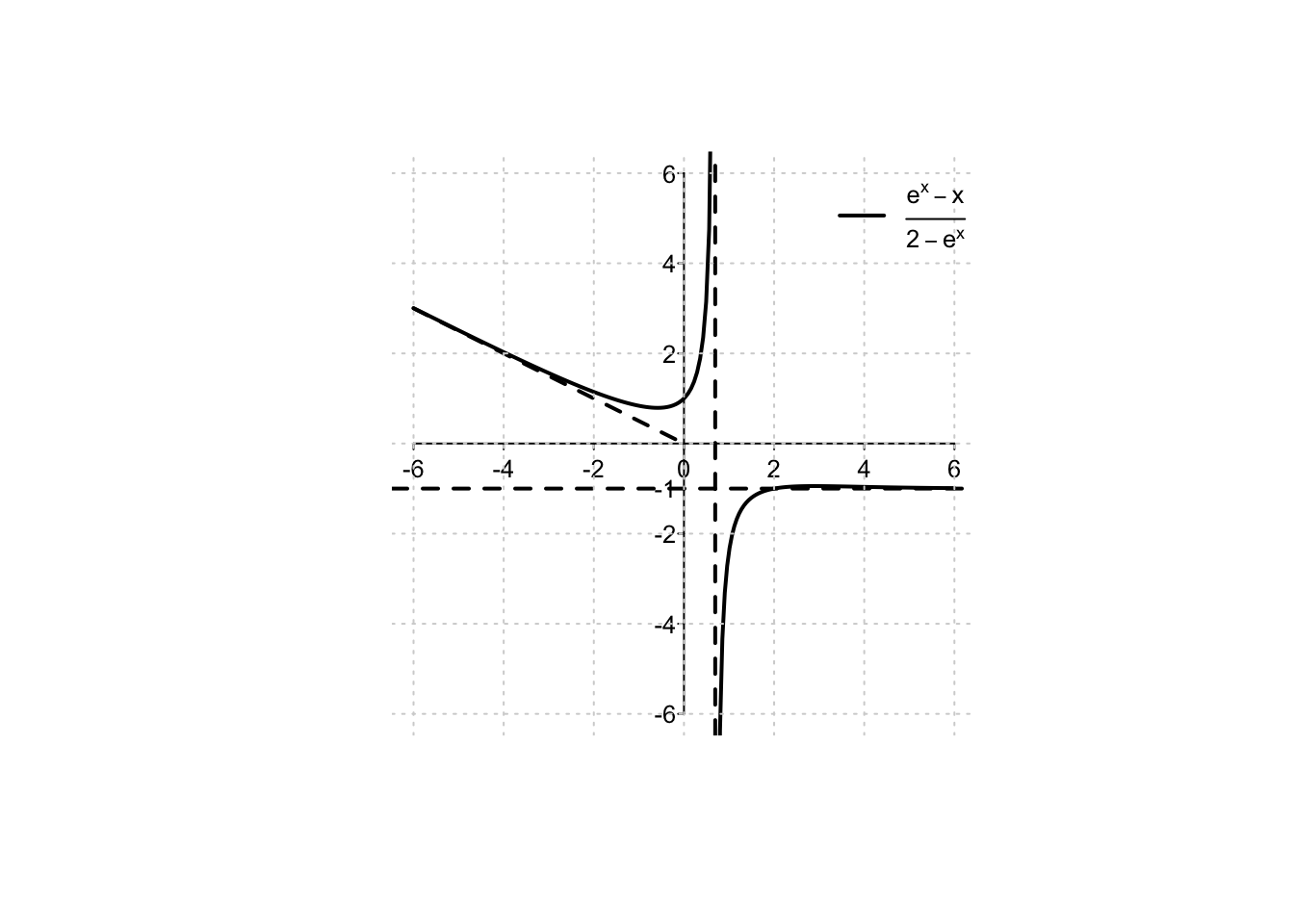
Example 3.14 Si trovino il dominio naturale $D_f$ e tutti gli eventuali asintoti della funzione $f:D_f\to \mathbb{R},$ \[ f(x)=\frac{e^x-x}{2-e^x}. \]

Ponendo il denominatore della frazione $2-e^x \neq 0$ si trova che $D_f=\mathbb{R} \setminus\{\log 2\}$.

È immediato constatare che nell’intorno di tale punto si verifica un limite di tipo (A), quindi un asintoto verticale. Infatti, nell’intorno del punto $x_0=\log 2$, il numeratore della funzione tenderà per continuità a $e^{\log 2}-\log 2= 2-\log2>0$ (ivi permanendo positivo), mentre il denominatore, funzione strettamente decrescente, cambierà il suo segno da positivo a negativo. Si ha quindi: \[ \lim_{x \to \log2^-} \,\frac{e^x-x \, (\mathbf{+})}{2-e^x\, (\mathbf{+})} = +\infty, \quad \lim_{x \to \log2^+} \,\frac{e^x-x \, (\mathbf{+})}{2-e^x\, (\mathbf{-})} = -\infty. \] Per $x \to +\infty$ si calcola facilmente che \[ \lim_{x \to +\infty} \,\frac{e^x-x}{2-e^x} = \lim_{x \to +\infty}\, \frac{\,\,\,\,\,e^x}{-e^x}= -1, \] quindi il grafico della funzione presenterà un asintoto orizzontale di equazione $y=-1$.

Dato che la funzione esponenziale è infinitesima per $x \to -\infty$, si calcola \[ \lim_{x \to -\infty}\, \frac{e^x-x}{2-e^x} = \frac{-x}{2}=+\infty. \] È lecito chiedersi quindi se il grafico della funzione presenti un asintoto obliquo per $x \to -\infty$. Si verifica quindi la prima condizione della definizione, ottenendo: \[ \lim_{x \to -\infty} \,\frac{e^x-x}{2x-xe^x} = \lim_{x \to -\infty}\, \frac{x\left(\frac{e^x}{x}-1\right)}{x(2-e^x)}= \lim_{x \to -\infty}\, \frac{\frac{e^x}{x}-1}{2-e^x}=\frac{0-1}{2-0}=-\frac{1}{2}=m; \] quindi la seconda: \[\begin{align*} &\lim_{x \to -\infty} \,\frac{e^x-x}{2-e^x}-\left(-\frac{1}{2}x\right)=\lim_{x \to -\infty}\, \frac{e^x-x}{2-e^x}+\frac{x}{2}=\lim_{x \to -\infty}\, \frac{2e^x-2x+2x-xe^x}{2(2-e^x)}\\ \\ =&\lim_{x \to -\infty}\, \frac{2e^x-xe^x}{4-2e^x}=\lim_{x \to -\infty}\, \frac{e^x(2-x)}{e^x(4e^{-x}-2)} =\lim_{x \to -\infty} \,\frac{2-x}{4e^{-x}-2}=\lim_{x \to -\infty} \,\frac{-x}{4e^{-x}}=0. \end{align*}\] Ne risulta che il grafico della funzione possiede anche un asintoto obliquo per $x \to -\infty$ (differente quindi dall’asintoto esistente per $x \to +\infty$) di equazione $y=-\frac{1}{2}x$. Tutti gli asintoti trovati possono essere verificati nel grafico seguente.

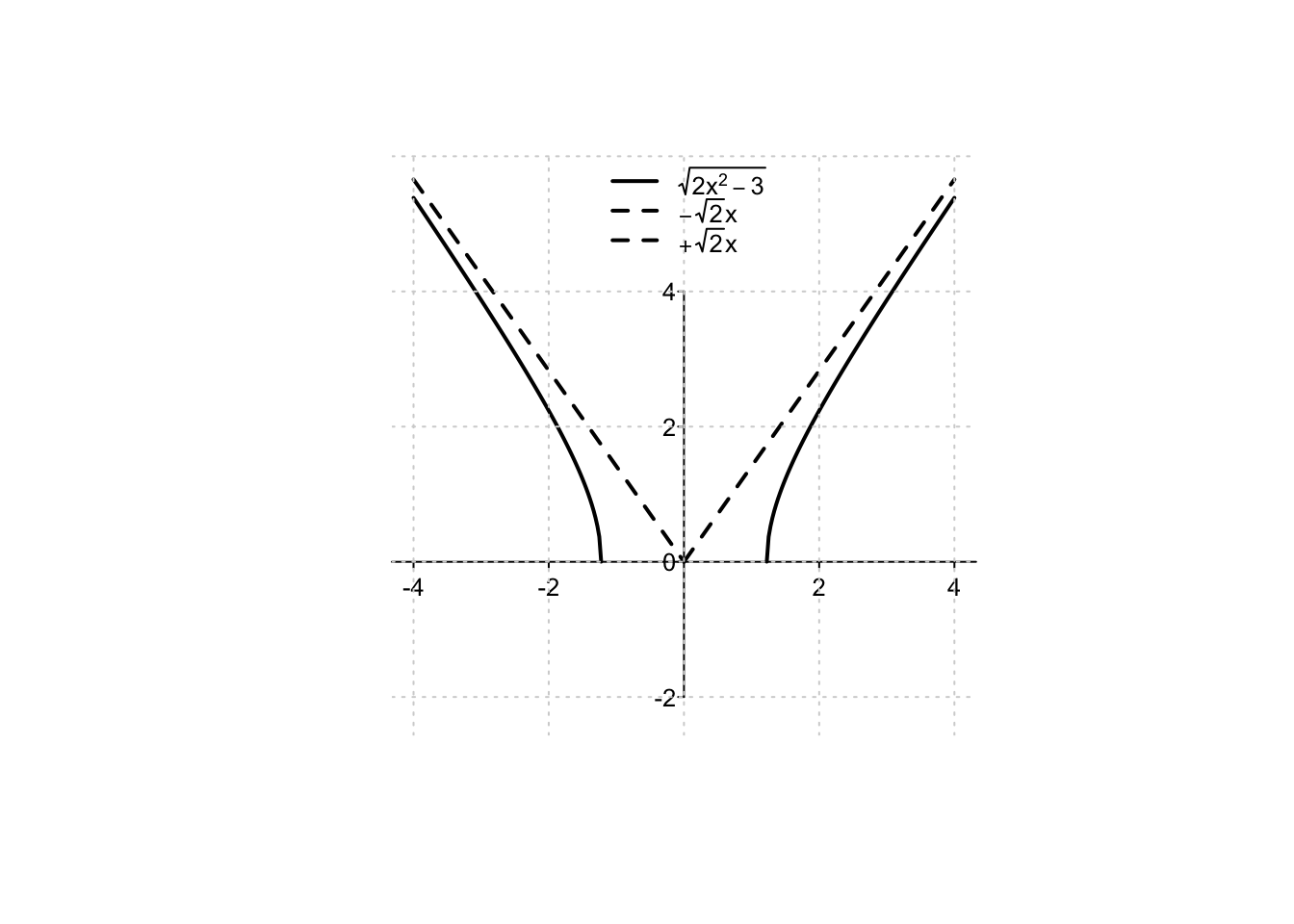
Example 3.15 Si trovino il dominio naturale $D_f$ e tutti gli eventuali asintoti della funzione $f:D_f\to \mathbb{R},$ \[ f(x)=\sqrt{2x^2-3}. \] La funzione è ben definita se l’argomento della radice quadrata è non negativo, cioè se $2x^2-3 \geq 0$. Si ha che il dominio naturale è l’insieme $D_f=\left(-\infty,-\sqrt{\frac{3}{2}}\,\right]\cup \left[\,\sqrt{\frac{3}{2}},+\infty\right).$ Dato che $\lim_{x \to +\infty} \sqrt{2x^2-3}=+\infty$, è possibile che il grafico della funzione abbia un asintoto obliquo. Si verifica quindi la prima condizione della definizione di asintoto obliquo: \[ \lim_{x \to +\infty}\, \frac{\sqrt{2x^2-3}}{x}=\lim_{x \to +\infty} \,\frac{\sqrt{2x^2}}{x}=\lim_{x \to +\infty} \,\frac{\sqrt{2}x}{x}=\sqrt{2}=m; \] quindi la seconda condizione: \[ \lim_{x \to +\infty} \sqrt{2x^2-3}-\sqrt{2}x. \] Si riconosce in questo limite un caso (B2) che va trattato come \[\begin{align*} \lim_{x \to +\infty} \,(\sqrt{2x^2-3}-\sqrt{2}x) \frac{(\sqrt{2x^2-3}+\sqrt{2}x)}{(\sqrt{2x^2-3}+\sqrt{2}x)}&=\lim_{x \to +\infty}\, \frac{2x^2-3-2x^2}{(\sqrt{2x^2-3}+\sqrt{2}x)}\\&=\lim_{x \to +\infty} \,\frac{-3}{(\sqrt{2x^2-3}+\sqrt{2}x)}=0. \end{align*}\] Per $x \to +\infty$, il grafico di $f$ ha quindi come asintoto obliquo la retta $y=\sqrt{2}x$. Per capire cosa succede per $x \to -\infty$, è sufficiente notare che la funzione $f$ è pari, quindi simmetrica rispetto all’asse delle ordinate. Disegnandone il grafico, si verifica immediatamente che per $x \to -\infty$, il grafico di $f$ avrà come asintoto obliquo la retta $y=-\sqrt{2}x$. Si possono verificare le corrispondenti condizioni per $x \to -\infty$.

3.10 Esercizi

In un tema di esame verrà richiesto di calcolare i limiti nei punti di frontiera del dominio naturale di una funzione data, includendo se possibile i punti $x=\pm \infty$.

Per gli esercizi sul calcolo degli asintoti obliqui, si rimanda al Capitolo 5.

Si calcolino i limiti delle seguenti funzioni $f: D_f \to \mathbb{R}$ nei punti di frontiera del dominio naturale $D_f$, includendo se possibile i punti $x=\pm \infty$. Si cerchi di individuare dapprima la casistica corrispondente tra quelle trattate (A), (B), (B2), (C), quindi di risolvere i limiti svolgendo il minor numero di calcoli possibili. Se un limite non esiste, si indichino come soluzione i limiti sinistro e destro.

Exercise 3.1

$f(x)= \frac{(x-3)}{(x-2)^2}$

Exercise 3.2

$f(x)= \frac{-5x^2+x}{e^x}$

Exercise 3.3

$f(x)= \frac{x^2-4x+1}{x}$

Exercise 3.4

$f(x)= \log \left( \frac{2-x}{x-4} \right)$

Exercise 3.5

$f(x)= \sqrt{x^2-2x}-x$

Exercise 3.6

$f(x)= \frac{e^{1-x}}{(x-2)^2}$

Exercise 3.7

$f(x)= \frac{-2\log(x^3)}{x^2}$

Exercise 3.8

$f(x)= \frac{-x^2+x+1}{e^x}$

Exercise 3.9

$f(x)= \frac{x^4-2x^2+1}{x^3+1}$

Exercise 3.10

$f(x)= \frac{3-\sqrt{x-3}}{12-x}$

Exercise 3.11

$f(x)= \frac{x^2+1}{x-1}$

Exercise 3.12

$f(x)= \frac{\sqrt{x}}{1-x}$

Exercise 3.13

$f(x)= \sqrt{x^2-9}-x$

Exercise 3.14

$f(x)= \frac{x+1}{1+x^2}$

Exercise 3.15

$f(x)= \frac{1-e^x}{e^x-2}$

Exercise 3.16

$f(x)= e^{\frac{x+1}{x}}$

Exercise 3.17

$f(x)= \frac{x^3}{-x^2+x+2}$

Exercise 3.18

$f(x)= \frac{\log(x^2-4)}{4-x^2}$

Exercise 3.19

$f(x)= -3x + \sqrt{x^2-9}$

Exercise 3.20

$f(x)= \log \left( \frac{6-x}{x-3} \right)$

Exercise 3.21

$f(x)= \frac{2x^2-2x-2}{x-2}$

Exercise 3.22

$f(x)= \frac{e^{x-4}}{3-x}$

Exercise 3.23

$f(x)= \frac{3x^3-2x^2-1}{(x-1)^2}$